水泥土复合式支护结构的综合刚度矩阵法

上官士青，杨 敏，刘尊景，蔡伟铭

（1.同济大学 土木工程学院，上海200092；2.中国电建集团华东勘测设计研究院有限公司，浙江 杭州310000；3.同济大学建筑设计研究院有限公司，上海200092）

水泥土搅拌桩重力式挡墙是软土地区常用的支护形式.但单纯的重力式挡墙作支护往往变形较大，常设置内支撑来控制位移，这是极为有效的［1］.当设置有内支撑时，墙体内会产生较大弯矩，为了防止墙身破坏，需要在墙体内使用钻孔灌注桩或型钢来加强，如果使用混凝土桩，则整个体系就组成了混凝土桩水泥土墙复合式围护结构.水泥土复合式支护结构首先由蔡伟铭提出，上世纪90年代在软土地区就有一些应用［2］；但因为缺少对其受力机理和变形规律的认识，没有形成与之配套的变形分析方法，实际应用中无完整设计方法可循，一直以来尚没有上升为一种应用广泛的基坑围护工法.

文献［1-5］对水泥土复合式支护结构或类似支护结构的设计及变形计算进行了研究.这些学者主要将该围护结构作为重力式挡墙进行设计计算，着重于在墙体刚性假设下计算墙角的转角和墙角的水平位移，再计算墙体的弯曲，将两种位移相互叠加.采用上述计算思路的原因主要是考虑该种支护形式源于重力式挡墙.在单纯的重力式挡墙设计计算中，主要依靠墙身自重来抗衡主动土压力，但现在的水泥土复合式支护结构经常配合内支撑来减小变形，同时墙内也增加了灌注桩来增加抗弯刚度，并不完全依靠墙身自重来抗衡土压力.随着社会发展，开挖深度越来越大，此类复合式支护结构设计开挖高度已超过7m，从形式上偏向于排桩支护发展，因此可尝试采用目前广泛流行的弹性支点法进行设计工作.如文献［6-8］的研究成果均摆脱了刚体重力式挡墙的变形计算思路，采用弹性支点法或位移函数法进行计算.笔者基于复合式重力挡墙自身的几何特性，考虑桩-墙相互摩擦作用，推导了其综合刚度矩阵.

1 计算模型

按图1中模型计算复合式支护结构变形.图中，q为坑外超载，pak为主动土压力，ps为被动土压力，Fh为内支撑反力.坑内开挖面以上的内支撑以弹性支座模拟；坑内开挖面以下作用在复合式支护结构上的土抗力以水平弹簧支座模拟；根据文献［9］，参考重力式基础的特性在墙底垂直方向设置一组弹簧.该弹簧最终换算为桩底节点转角自由度上的刚度.同样地，水泥土墙底部与土体的水平摩擦应予以考虑，该水平摩擦弹簧可按基坑规范中重力式挡墙部分计算.由于在实际计算中，采用复合梁单元对复合支护结构进行计算，而梁单元是无体积的，可将水泥土墙底部的水平摩阻力弹簧与图1中的被动土压力弹簧3在挡墙底部节点并联.图1中复合式支护结构采用考虑混凝土桩和水泥土墙摩擦作用的综合梁单元进行模拟.

图1 物理模型图Fig.1 Physical model

综合梁单元及其综合刚度矩阵是在平面简单梁单元（4自由度）理论的基础上发展而来，推导刚度矩阵时新增的假设及相关内容说明如下：

（1）公用轴线假设.假设1个基坑剖面中水泥土搅拌桩（墙）与混凝土桩水平位移相同，即水泥土桩与混凝土桩的轴线变形相同.因此两种桩型在计算时按1根地基梁计算.

（2）综合刚度假设.如按1根梁单元计算复合式支护结构的变形，需推导它们的综合刚度矩阵.本文按照能量原理和驻值原理推导刚度矩阵.在传统梁单元刚度矩阵推导过程中考虑混凝土桩的弯曲应变能、水泥土搅拌桩（墙）的弯曲应变能的基础上，增加了对混凝土桩的拉伸应变能和混凝土桩与水泥土体摩擦力（弹簧）做功的考虑.由于在弹性支点法的框架下，难以计算单元质点垂直方向上的位移，刚度矩阵中不考虑重力势能的改变.

（3）混凝土桩与水泥土体摩擦力作用距离假设.在现有梁单元位移函数下，引入新自由度——混凝土桩与水泥土体摩擦力作用距离，用于计算复合支护结构内部摩擦做功.由于引入了新自由度，新的综合单元自由度为6个.笔者设定1个梁单元包括2个节点，每个节点包括3个自由度：单元上、下节点挠度u1，u2，单元上、下节点转角θ1，θ2，单元上、下节点处水泥土墙与混凝土桩的相对滑移量（包含水泥土剪切位移和相对滑移）Δ1，Δ2.

（4）在新自由度基础上，通过引入开放性摩擦弹簧计算摩阻力的大小.复合式支护结构墙身由水泥土墙和混凝土钻孔桩组成.计算时考虑水泥土墙与混凝土桩之间存在一系列的切向弹簧，并假设弹簧是线性的（见图2）.这些摩擦弹簧的伸长量定义为引入的新自由度Δ1，Δ2.该自由度与其他2个自由度之间的位移协调通过平截面假定和节点转角θ1，θ2进行表述.

图2 水泥土墙与混凝土桩协同工作分析图Fig.2 Cement wall and concrete pile interaction

2 综合刚度矩阵的推导

2.1 单元位移函数

单元位移函数包括水泥土墙单元弯曲的位移函数及混凝土桩单元压缩的位移函数.其中，单元弯曲的位移函数表示单元内部坐标与水泥土墙挠度的关系；混凝土桩单元压缩的位移函数表示单元内部坐标与混凝土桩身垂直方向位移的关系.根据第1节说明（1），水泥土墙和混凝土桩的弯曲位移函数相同.

2.1.1 水泥土墙分析

假设水泥土墙为纯弯曲状态，引入常规简单梁单元（二节点Hermite单元）的形函数

式中：内部坐标ξ=（x-x1）／l；l为单元长度；x为外部坐标；x1为单元节点外部坐标.

则得到水泥土墙位移函数的简单表达式为

将形函数（1）代入到单元位移函数（2）中，得到如下自由度和单元内部坐标表示的单元位移函数：

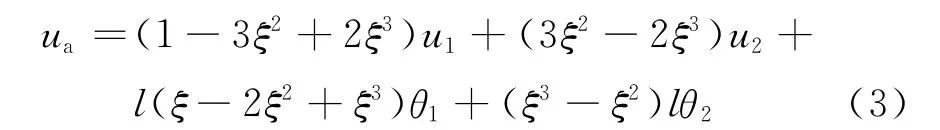
2.1.2 混凝土桩分析

对混凝土桩进行分析，研究其拉伸时的位移函数.为便于分析，这两个位移函数采用相同的内部坐标系（该坐标系为一维坐标系，两个位移函数表示的水泥土挠度及混凝土桩拉伸量是在该坐标系中变化的函数），因此内部坐标（系）ξ通用

由图3可见，连接弹簧连接了混凝土桩节点与按平截面计算得到的理论节点，因此该弹簧考虑了水泥土墙和混凝土桩桩身的摩擦.该连接弹簧的伸长为新引入的自由度Δ1，Δ2（对应于单元2个节点）.

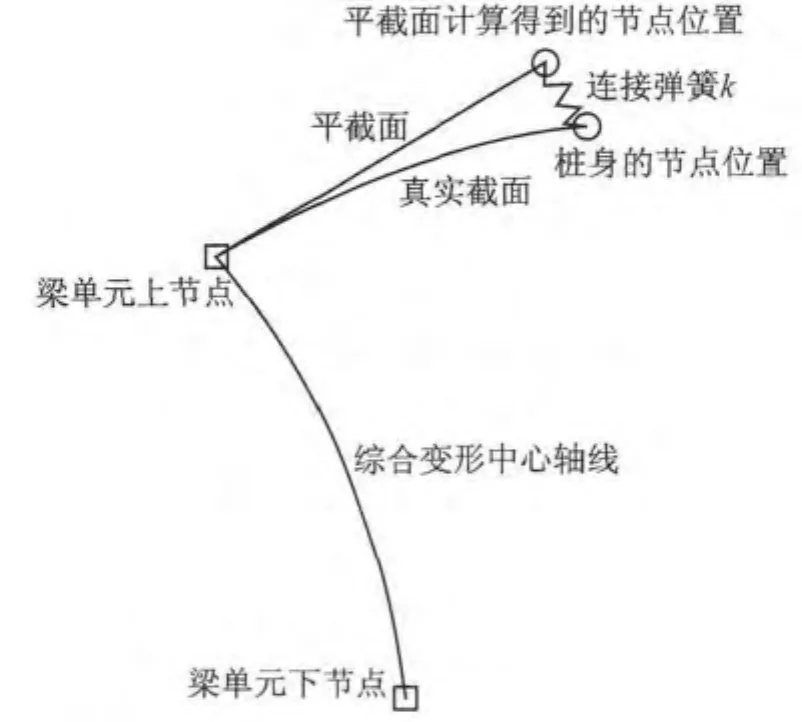
图3 水泥土墙与混凝土桩摩擦弹簧图Fig.3 Cement walls and concrete pile friction spring

由预设的6个自由度，根据平截面假定，可得到水泥土桩垂直方向上的坐标为x1+aθ1和x2+aθ2.其中，x1和x2是节点坐标，为已知量；a为偏心距，即混凝土桩中心与复合式挡墙弯曲中心的距离，可由a=B／2-c进行估算；B为墙体宽度；c为混凝土桩中心距离复合式挡墙近侧边的距离.引入桩土间滑移量修正，可得水泥土桩单元上、下节点的垂直方向坐标为x1+aθ1-Δ1和x2+aθ2-Δ2.由上述分析可知，这2个节点的位移量为aθ1-Δ1和aθ2-Δ2.由此可得位移函数

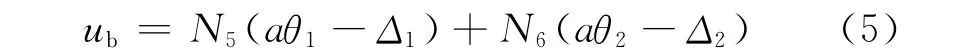
将形函数（4）代入式（5）可得混凝土桩拉伸的位移函数为

2.2 单元应变势能

单元应变势能由单元位移所包含的势能和弹簧势能组成.对式（3）求导数，得单元曲率

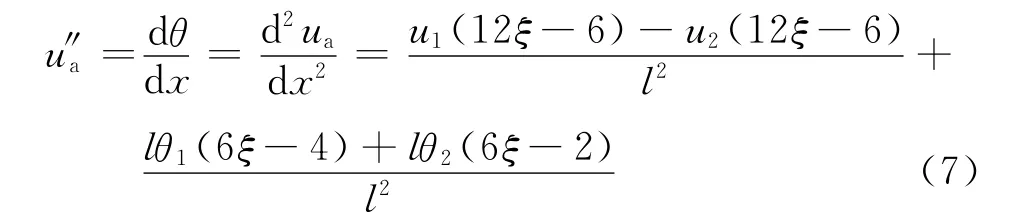
用式（7）来表达单元位移弹性势能W1，采用单元内定积分计算，可将单元内部坐标消除

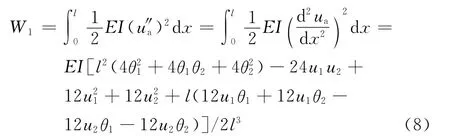
式中：EI为混凝土桩与水泥土墙抗弯刚度之和，kN·m2.

混凝土桩拉伸变形势能及摩阻力弹簧势能W2可由单元长度l内的应力应变积分计算

式中：E1A1为内插混凝土桩的抗拉刚度，kN；k1，k2分别为上、下节点混凝土桩与水泥土墙之间的摩擦弹簧刚度系数，kN·m-1.

式（6）代入式（9）换算为内部坐标系积分，消除内部坐标ξ，得

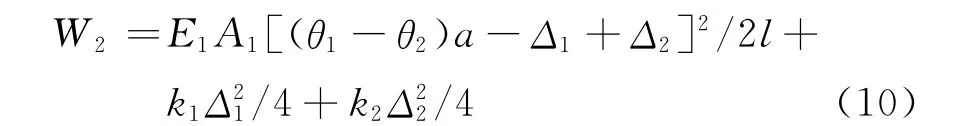
2.3 外力势能

外力势能W3可由下式计算：

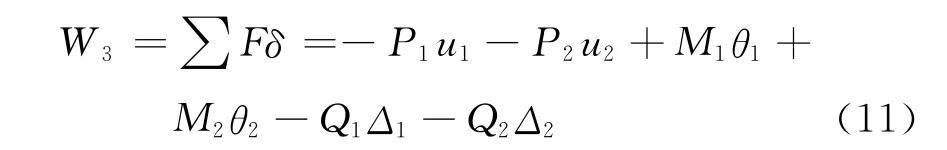
式中：P1为上节点u1对应的节点荷载，kN；P2为下节点u2对应的节点荷载，kN；M1为上节点θ1对应的节点荷载，kN·m；M2为下节点θ2对应的节点荷载，kN·m；Q1为上节点混凝土桩垂直方向自由度对应的节点荷载（总刚度矩阵拼装后一般为0），kN；Q2为下节点混凝土桩垂直方向自由度对应的节点荷载（总刚度矩阵拼装后一般为0），kN.

2.4 总势能

单元总势能W定义为单元应变势能和外力势能之和，可由式（8），（10），（11）计算

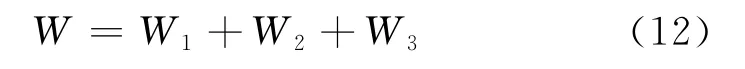
2.5 求偏导数

根据“驻值原理”对总势能式（12）求6个自由度的偏导数，并令偏导数等于0，得6个方程

2.6 刚度矩阵

将以上由驻值原理得出的偏导数方程式（13）写成如下刚度矩阵的形式：

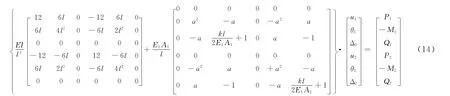
式中k1和k2写为k.可见综合刚度矩阵是由欧拉梁的刚度矩阵和一个耦合刚度矩阵组成的.应用于弹性支点法时，该矩阵的组装与常规杆件刚度矩阵相同，拼装简便，配合增量法或迭代法也可用于非线性弹性问题的计算.

3 刚度矩阵参数的确定

使用上述刚度矩阵计算复合式挡墙基坑围护结构的内力和变形，需要确定混凝土桩与水泥土墙摩擦弹簧刚度系数k.由于水泥土墙自身存在一定的剪切位移［10］，界面上的变形并不是单纯的滑移，因此该弹簧应为剪切位移等效弹簧ks（水泥土自身剪切变形弹簧）与桩身滑移弹簧kf（混凝土桩与水泥土墙截面上二者相对滑移弹簧）的串联，由静力下弹性弹簧的串联公式容易得出该串联弹簧的刚度为

为了工程计算的实用性，垂直受荷单桩的计算理论中往往采用单一弹簧计算，如剪切位移法不考虑桩土间相对滑移，荷载传递法往往不考虑剪切.本文采用剪切位移法［10-11］确定弹簧刚度系数.文献［11］给出的ks约比土体的剪切模量G大一个数量级.文献［12］指出在其嵌入桩（embeded pile）模型的桩土接触计算中，kf远大于土体的剪切模量G.上述分析表明ks是kf的10～100倍，因此对于串联后总刚度k约等于0.9～0.99倍的ks.因此本文主要考虑ks的作用，即k约等于ks.

分析图4桩侧土单元ABCD，当桩发生沉降S后，单元随之发生沉降，并发生剪切变形A′B′C′D′，将剪切力传递给相邻单元BCEF，这个传递过程连续进行一直传递到很远处的X点，距离桩轴线为rm=nr0，rm也是剪切位移法中桩的影响半径，在X点处由于剪切变形已很小可忽略不计，即

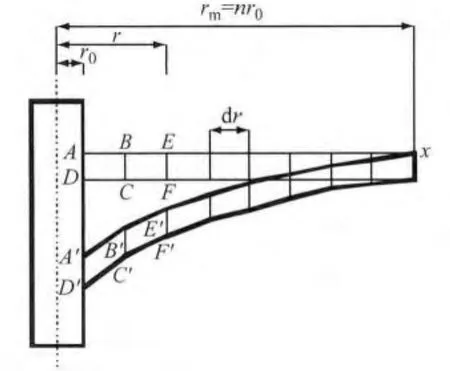
图4 剪切位移法桩身荷载传递模型Fig.4 Load transfer in shear displacement method

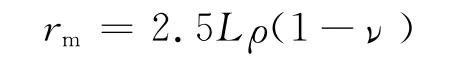
式中：L为桩身长度；ρ为不均匀系数；ν为泊松比.桩的影响半径计算公式是根据统计得来的经验计算公式，在统计时考虑不均匀系数作为折减，在没有统计数据时取ρ=1.

根据剪切位移法［10-11］，求得距离桩轴线r处土单元的剪切应变γ=dS／dr，其剪力τ为

式中，Gs为水泥土剪切模量.

根据平衡条件

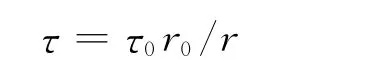
式中：τ0为桩表面的剪应力；r0为混凝土桩的半径.可得

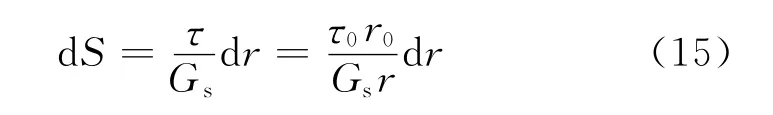
若土的剪切模量Gs为常数，则由式（15）可得桩侧沉降S的计算公式为

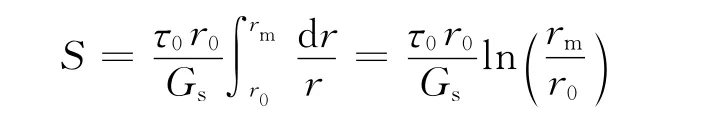
则弹簧刚度k可由下式进行估算：

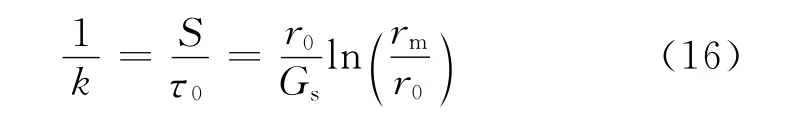
考虑到单桩荷载传递法计算常用弹性-理想塑性的连接弹簧，而本文方法不涉及非线性弹性计算，需要用弹性弹簧尽可能地模拟一个弹-塑性弹簧，故保守地Gs可取水泥土的剪切模量的一半.

4 算例

采用综合刚度矩阵对上海虹桥镇95号地块基坑工程C型试验段进行计算，其剖面图见图5.C型试验段处基坑开挖深度为6.4m，采用复合式水泥土挡墙围护（对撑）；水泥土墙采用双轴水泥土搅拌桩，水泥掺量为13%，墙高15m（第一排水泥土搅拌桩长16m，后排桩长15m，计算时按15m），宽度为3.2m；内插筋体为混凝土钻孔桩，桩长为12m，直径为600mm，桩间距为2m；钢支撑采用双拼Φ609×16钢支撑，支撑轴线位于地表以下1.5m，支撑间距9.9m，长度为52m；混凝土冠梁高0.7m，宽度为1.0m.土层参数见表1.

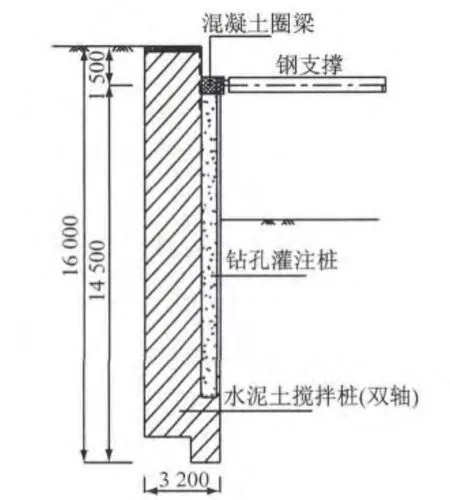
图5 支护结构剖面图（单位：mm）Fig.5 Sectional view of retaining structure（unit：mm）

偏心距a=B／2-c=1.1m.事实上，整个支护结构的弯曲中心并不在形心，该处计算是粗略的.

文献［13］给出了水泥土弹性模量E与无侧限抗压 强度fcu的经验关系，E=（200～300）fcu.fcu的常用值一般为1～2MPa.由于现场搅拌桩所处的真实环境和室内试块实验的养护条件不同，文献［14］指出水泥加固土的现场测试强度一般为室内试验强度的30%～50%.本文取E=200×50%×1.5MPa=150MPa作为计算时的杨氏模量.

表1 计算截面处的土层参数Tab.1 Soil parameters at cross section

剪切弹簧刚度的确定如下：影响半径rm=2.5Lρ（1-ν）=13.13m；水泥土剪切模量按弹性模量换算得G=57.69MPa；根据第3节的说明，对于Gs建议取剪切模量的一半.Gs=0.5G=28.85 MPa，则；考虑到桩间距为2m，单元长度为h，则单元弹簧刚度ke=0.5kπDh=2.49×104h.

按本文推导的刚度矩阵用弹性支点法计算，可得到墙体侧向变形、墙体转角、混凝土桩与水泥土墙剪切变形量、墙身剪力、混凝土桩身弯矩、混凝土桩身轴力.通过混凝土桩身轴力和混凝土桩身弯矩可对混凝土桩进行配筋计算.

图6中，仅考虑桩和考虑桩墙的两根变形曲线是采用简欧拉梁单元的刚度矩阵计算的，考虑桩、墙及其相互作用的曲线是通过本文推导的综合刚度矩阵计算的.可见，采用综合刚度矩阵计算时，由于考虑了墙与桩身的相互作用，复合挡墙的总体刚度比简单梁单元的刚度大，与现场实测更为接近.计算结果同时表明，仅将桩和墙体的抗弯刚度简单叠加用于常规梁单元，计算出的位移是偏大的.

图7中，通过刚度矩阵法计算得到的支撑轴力为213kN，现场监测得到的支撑轴力为205kN，二者相差不大.综合刚度矩阵包含有垂直方向的自由度Δ1，Δ2，相比传统弹性支点法，本文方法可计算得到垂直方向上混凝土桩身受拉变形和桩身轴力，见图8.以上对比显示出采用综合刚度矩阵法进行复合式挡墙内力和变形分析的有效性和合理性.

图6 墙体水平位移Fig.6 Horizontal displacement of the wall

图7 混凝土与水泥土墙承担的剪力Fig.7 Shear force of retaining wall and inner concrete pile

图8 混凝土桩的桩身轴力Fig.8 Axial force of inner concrete pile

水泥土的弹性模量涉及k的取值，对单元等效刚度具有重要影响，笔者同时选取110，130，150，170，190MPa进行了计算，考察该参数取值对计算结果的影响程度.计算结果如图9所示，随着水泥土模量的大幅度变化，支护结构最大水平位移仅有约3～4mm的变化幅度.这主要是因为复合式水泥土支护结构的抗弯是水泥土挡墙与混凝土桩共同作用的，单独改变水泥土挡墙的弹性模量并没有对最大水平位移值造成非常大的影响.

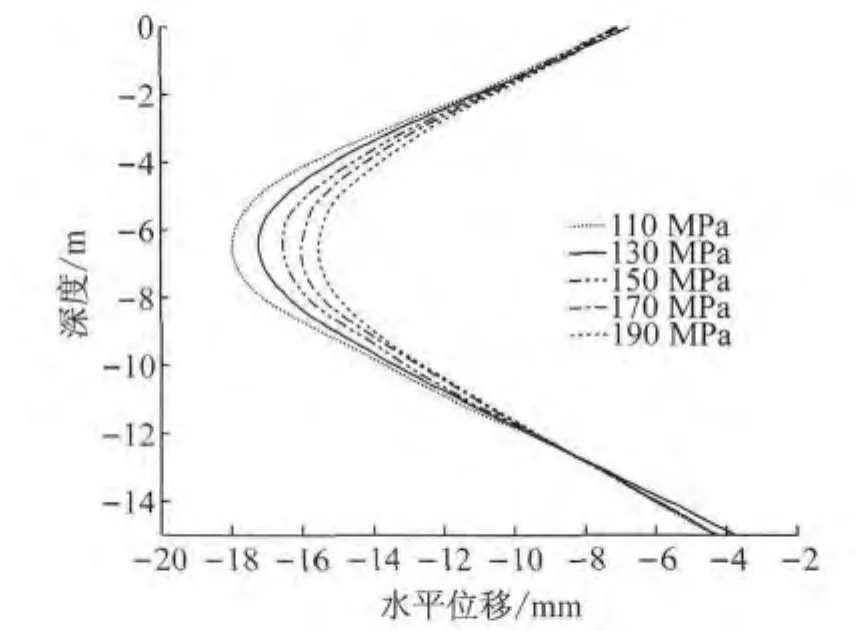
图9 不同水泥土弹性模量对水平位移的影响Fig.9 Effect of different elastic modulus of soil cement on horizontal displacement

5 结论

本文根据驻值原理推导了用于水泥土复合支护结构的综合刚度矩阵.通过引入新的自由度——混凝土桩与水泥土体摩擦力作用距离，在刚度矩阵的推导过程中考虑了混凝土桩的拉伸与墙桩相互摩擦，得到了6×6的综合刚度矩阵.算例表明，在复合式支护结构的计算中，相比常规梁单元刚度矩阵，该综合刚度矩阵计算结果更为合理.

［1］ 冯又全，杨敏，熊巨华.水泥土复合式围护结构的位移内力计算与性状分析［J］.岩土工程技术，1999（3）：3.FENG Youquan，YANG Min，XIONG Juhua.Displacement and internal force calculation as well as behavior analysis of cement soil composite retaining structure［J］.Geotechnical Engineering Technique，1999（3）：3.

［2］ 蔡伟铭.一种新型围护结构——复合型挡墙［J］.地基基础工程，1997，7（4）：16.CAI Weiming.A new type of retaining wall：Composite retaining wall［J］.Foundation Engineering，1997，7（4）：16.

［3］ 熊祚森，杨林德，黄宏伟.水泥土复合式支挡结构的机理分析［J］.土木工程学报，1997，30（5）：43.XIONG Zuosen，YANG Linde，HUANG Hongwei.Analysis of the mechanism of cement-soil composite retaining structure［J］.China Civil Engineering Journal，1997，30（5）：43.

［4］ 黄广龙，惠刚，方乾，等.MC桩组合支护结构设计与应用研究［J］.岩土力学，2009，30（9）：2697.HUANG Guanglong，HUI Gang，FANG Qian，etal.Design of MC composite retaining structure and its application［J］.Rock and Soil Mechanics，2009，30（9）：2697.

［5］ 阮伟光.水泥土挡墙加钻孔灌注桩组合体的研究［D］.广州：华南理工大学，2005.RUAN Weiguang.Study on the combination of cement-soil retaining wall and bored piles［D］.Guangzhou：South China University of Technology，2005.

［6］ 宰金璋，朱百里.水泥土挡墙的变形及其计算［C］∥第四届全国地基处理学术讨论会论文集.杭州：浙江大学出版杜，1995：529-533.ZAI Jinzhang， ZHU Baili.Cement-soil retaining wall deformation and its calculation［C］∥Proceedings of Fourth National Conference on Foundation Treatment.Hangzhou：Zhejiang University Press，1995：529-533.

［7］ 陆瑞明，李红.水泥土挡墙的空间作用研究［J］.工程勘察，1997（1）：1.LU Ruiming，LI Hong.The study of space effect of the cementsoil retaining wall［J］.Geotechnical Investigation and Surveying，1997（1）：1.

［8］ 王卫东，王浩然，黄茂松，等.水泥土重力式围护结构水平变形简化计算方法［J］.同济大学学报：自然科学版，2011，39（6）：814.WANG Weidong，WANG Haoran，HUANG Maosong，etal.Simplified calculation method of lateral deformation of gravity retaining wall［J］.Journal of Tongji University： Natural Science，2011，39（6）：814.

［9］ 杨敏，熊巨华.水泥土围护结构的稳定性与变形分析［C］∥中国土木工程学会第八届土力学及岩土工程学术会议论文集.北京：万国学术出版社，1999：647-650.YANG Min，XIONG Juhua.The stability and deformation analysis of the cement-soil retaining structure［C］∥Proceedings of the 8th Soil Mechanics and Geotechnical Engineering Conference of China Civil Engineering Society.Beijing：International Academic Publishers，1999：647-650.

［10］ Randolph M F， Wroth C P.An analysis of the vertical deformation of pile groups［J］.Geotechnique，1979，29（4）：423.

［11］ Kraft L M，Kagawa T，Ray R P.Theoreticalt-zcurves［J］.Journal of the Geotechnical Engineering Division，1981，107（11）：1543.

［12］ Brinkgreve R B J，Swolfs W M.Plaxis 3D foundation version 2 user's manual［Z］.Delft：Plaxis BV，2007.

［13］ 朱家祥.深基坑工程中混凝土芯水泥土桩水平承载机理与变形特性研究［D］.南京：河海大学，2008.ZHU Jiaxiang.Pile horizontal bearing mechanism and deformation characteristics of concrete-cored pile in excavation［D］.Nanjing：Haohai University，2008.

［14］ 贾坚.影响水泥土强度的综合含水量研究［J］.地下空间与工程学报，2006，2（1）：132.JIA Jian.Research on comprehensive water content of cement treated soil［J］.Chinese Journal of Underground Space and Engineering，2006，2（1）：132.