基于BP神经网络的南平公交综合评价模型研究

陈桂福 陈丹妮

（1.中国市政工程西北设计研究院有限公司，甘肃 兰州 730000；2.安溪县农村信用合作联社，福建 安溪 362400）

公交综合评价模型的研究，有利于城市公交规划评价体系的发展和完善，能够为南平中心城区公交规划提供参考和方向。南平中心城区交通总体水平如下：从2000年至2010年，南平市延平区的机动车保有量从不足13000量增加至100000余量，增幅达681%。截至2014年6月调查数据，南平市中心城区公交车辆的平均速度为16km/h；中心城区不同交通方式的平均出行时耗：步行18.83分钟/次，公交车26.16分钟/次，出租车9.9分钟/次，自行车21.63分钟/次，摩托车16.95分钟/次，私家车19.87分钟/次，电动车14.52分钟/次；南平市现状公交分担率为11.31%。对于公交综合评价，目前主要是采用层次分析法、专家咨询法或模糊理论方法建立非线性模型来求解。但是，层次分析法、专家咨询法受主观因素影响较大，一旦有些评价因素发生变化时，就会产生较大的误差，必须重新建立模型，以往的一些经验性知识也得不到充分利用。而BP神经网络具有自学习、自适应能力和强容错性，是一种多层次反馈型网络，能较好地模拟评价专家进行综合评价的过程，因而具有广泛的应用前景。本文利用人工神经网络的理论，结合南平公交规划，筛选出10项相对重要的评价指标，利用神经网络自组织、自学习的能力，在评价指标和评价结果之间建立了一定关系，从而实现了基于神经网络的南平公交综合评价模型。实例预测结果，精度误差都在较为理想的范围内，因此，针对南平得到的预测结果是可以接受的，从而，也为南平交通的发展提供参考的依据。

图1 南平中心城区交通总体层面评价指标Figure 1 Evaluation index of nanping city traffic center overall level

1 BP人工神经网络的介绍[1]

反向传播（Back Propagation，BP）神经网络是由Rumelhart等人于1985年提出的一种具有自学习、自组织的神经元模型，它是一种多层次反馈型网络，所使用的是有“导师”的学习算法。BP神经网络是一种具有三层或三层以上的层次结构网络，相邻上、下层之间各神经元实现全连接，即下层的每个神经元与上层的每个神经元都实现权相连，而每层神经元之间无连接。BP算法不仅具有输入层节点、输出层节点，还可有一个多个隐含层节点。典型的3层BP神经网络模型如图2。

图2 3层BP神经网络结构图Figure 2 Structure of three layers of BP neural network

对于输入信号，要先向前传播到隐含层节点，经作用函数后，再把隐节点的输出信号传播到输出节点，最后给出输出结果。在BP算法中，节点的作用的激励函数通常选取S型函数。对于BP模型的输入层神经元，其输出与输入相同。中间隐含层和输出层的神经元的操作规则如下：

式中：Yk-li是k-1层第i个神经元的输出，也是第k层神经元的输入；

Wk-li,kj是k-1层第i个元素与k层第j个元素的连接权值；

Ykj是k层第j个神经元的输出，也是第k+1层神经元的输出；

f是Sigmoid 函数。 F（μ）=1/（1+e-μ）。

2 南平中心城区公交系统评价的BP网络模型设计

2.1 评价指标的选取

2000年，公安部和建设部制定《城市道路交通管理评价体系》，对公共交通评价指标作出了系统的归纳，笔者结合南平中心城区公共交通发展规划的项目，从2007年“畅通工程”评价指标体系中提炼了10项相对重要的评价指标作为模型的输入项目。评价指标的选取与设置直接影响评价结果，对评价指标的选取遵循两个原则：

①站在交通专家的角度来考虑是否能全面有效地反映公交系统的效率；

②站在南平政府的角度来考虑能否对南平公共交通的发展有推动作用。

根据以上原则建立的南平中心城区公交评价体系如图3。

2.2 构建评价模型

应用BP神经网络对南平中心城区公交系统进行综合评价的基本研究思路是：将反映公交系统的各种评价指标作为输入向量，将综合评价结果作为神经网络的输出，从而建立了一个BP神经网络模型。将国内主要城市的评价指标和综合评价结果作为训练网络的样本，从而使网络通过自主学习建立正确的内部关系。训练好的神经网络可用于城市公交系统评价的预测和平时的自我测试。

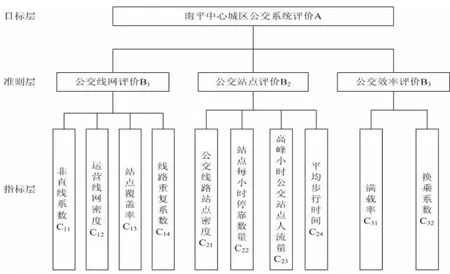
图3 南平中心城区公交评价体系层次结构示意图Figure 3 Structure schematic drawing of bus evaluation system in the nanping city

我们将模型的输出结果分为5个评价等级：极差、较差、一般、良好、高。评价集与评语集对应对应表如表1。因为神经元作用函数值域为[0，1]，所以评价集采用[0，1]数值。

表1 评价集与评语集对应表Table 1 Corresponding table of evaluation set and comments set

隐含层的单元数目的选择可以参考公式（2）选取[2]。

式中：m为输出神经元数，n为输入单元数，a为 [1，10]之间的常数。根据公式（2），并经过反复测试，最终确定隐含层数目为8。综合评价模型的结构为10-8-1，如图4所示。

图4 综合评价模型Figure 4 Comprehensive evaluation model

3 综合评价模型的BP网络模型实现和应用

3.1 样本和输入数据的规范化处理

对国内主要城市公交评价指标数据（共14个样本），其中8个样本作为学习样本，5个样本作为测试样本，用来进行精度的检验，从而得到可靠的模型。最后输入南平数据进行综合评价。

由于转移函数值域为[0，1]，因此必须先对数据进行归一化处理[1]。公交评价指标一般有以下几种类型：成本型、效益型、适度型和区间型。

对于X中的n个指标，

①成本型标准化函数（其值越小越好）

②效益型标准化函数（其值越大越好）

③适度型标准化函数（指标值以稳定再某一固定值为佳）

式中：Xmid为最合适值。

④区间型标准化函数，（其值以落在某个区间为最佳的指标）

式中：[q1，q2]为该指标的最佳稳定区间。

3.2 BP网络学习算法的Matlab实现

构建的神经网络[2]模型输入层有10个神经元，隐含层有8个神经元，隐含层传输函数为tansig，输出层是传输函数采用logsig；同时为了提高学习效率，将学习速度设置为0.2；而训练步数的大小将在一定程度上影响学习的效果，故设置训练步数为 10，20，40，50，80，100，200，400，500，…，分别观察其拟合效果，发现，当训练步数为500时，能较好地拟合数据，继续增大步数，数据又会产生较大的震荡，拟合精度也较低，因此，训练步数采用500。目标误差为0.00001。

通过建立的网络模型，将测试样本的输入值代入模型，得到的预测值与专家的评价值对比表如表2。

表2 模型测试结果比较及预测Table 2 compare and prediction of model test results

图5 训练结果（训练函数：traingd）Figure 5 Training results（training function:traingd）

图6 模型预测值Figure 6 Model prediction

4 结果与讨论

（1）根据《华普城市畅行指数-中国城市畅行指数2006年度报告》[3]，国内城市的平均得分为54.1，根据预测得到的数据，南平中心城区公交水平的综合得分为43.81，评价结果为一般，与全国的平均水平还是有很大的差距。

（2）公交综合评价是一个复杂的非线性问题，而神经网络具有较强的的自组织、自适应和自学习能力，对南平公交的综合评价效果良好，不但客服了人工评价的主观性及模糊随机性的影响，也具有较强的动态性，可以进一步的跟踪学习。

（3）由于受资料来源的限制，本文所采用的指标为国内主要城市的数据，样本容量也不够大，虽然不影响网络的理论应用，神经网络也有较强的容错性，但不同类型的城市指标数据还是会对模型的自主学习产生一定影响。因此，在运用神经网络进行城市类型的聚类分析与指标的选择上还有待于进一步研究。

（4）人工神经网络作为一种新兴的理论，具有运算速度快、求解问题的效率高、自主学习能力强、适应面宽等优点，能较好地模拟专家进行综合评价的过程，在实际中得以大量的应用，解决了很多利用传统方法难于解决的问题[4]。但目前总体而言其在城市公共交通综合评价领域的研究还处于起步状态，仍有许多问题需要进一步研究。

［1］杜栋，庞庆华.现代综合评价模型方法与案例精选[M].北京:清华大学出版社，2005:86-110.

［2］葛哲学，孙志强.神经网络理论与MATLAB R2007[M].北京:电子工业出版社，2007:111-112.

［3］百度文库.2012-5-26.华普城市畅行指数-中国城市畅行指数2006年度报告.http://wenku.baidu.com/view/6d91662de2bd960590c67778.html.

［4］陈桂福，陈丹妮.基于VISSIM的山区高速公路隧道入口段行车安全分析[J].江西建材，2014（22）：178-180.