冲击荷载作用下含水泥质粉砂岩的损伤规律研究

詹金武，张乃烊，黄 明，张冰淇

（1.北京交通大学土木建筑学院，北京100044；2.福州大学土木工程学院，福州350108）

冲击荷载作用下含水泥质粉砂岩的损伤规律研究

詹金武1，张乃烊2，黄 明2，张冰淇2

（1.北京交通大学土木建筑学院，北京100044；2.福州大学土木工程学院，福州350108）

采用分离式霍普金森压杆（SHPB）试验装置，对泥质粉砂岩进行了不同含水状态下的动态力学性能试验，分析了含水率变化对泥质粉砂岩动力特性的影响，并基于连续损伤理论及统计强度理论建立了泥质粉砂岩的动态损伤力学模型，得到了相应的损伤演化规律。研究结果表明，采用基于Weibull分布建立的动态时效损伤模型，其理论拟合曲线与实测曲线具有较好的一致性，损伤参数F0与弹性模量及冲击速度有一定的相关性，弹性模量越大，损伤参数F0也越大，含水率的变化对岩石动力特性具有较大的影响。

SHPB；泥质粉砂岩；冲击速度；含水状态；损伤模型

随着我国经济的快速发展，出现了越来越多涉及到岩石的动态力学性能及动态破坏的问题［1-4］，如矿山开采、隧道开挖、常规爆炸及核爆防护工程，以及滑坡、地震、岩爆等自然灾害都涉及到的岩石动力破坏问题，使得开展这方面的研究成为必要。岩石在冲击载荷作用下，其表征出来的力学特性与静载作用下存在显著的差异。如在隧道工程凿岩爆破过程中，围岩承受的外力均为冲击载荷，相比静力荷载作用，冲击动荷载作用下围岩内部形成的应力场及位移场有较大的差异。国内外学者针对岩石的动力特性开展了较多的研究，在考虑损伤影响的基础上，建立了损伤本构模型［5-9］。郑永来和夏颂佑［7］在鲍埃丁流变模型的基础上提出黏弹性连续损伤本构模型。谢理想等［8］对修正的过应力模型本构方程进行简化，得到简化的损伤过应力模型本构方程，并对实测曲线进行拟合，结果实测曲线与拟合曲线具有很好的一致性。朱晶晶等［9］利用改进的大直径SHPB装置，对花岗岩试件进行单轴循环冲击压缩试验，建立了基于Weibull分布的动态时效损伤模型，模型计算结果与试验实测结果具有较好的一致性。

然而，以往的试验大多集中考虑应变率对试验结果的影响，鲜见针对含水状态变化对岩石动力特性的影响研究。水是影响岩石力学性质的一个不可忽略的因素，在大多数工程活动中，水都是一个重要的参与者，因此，有必要开展含水率变化对岩石动力学性能的影响。本文以泥质粉砂岩为研究对象，利用大直径SHPB装置进行常规的单轴冲击压缩试验，研究含水状态及冲击速度的变化对试验结果的影响，并基于连续损伤理论及统计强度理论建立泥质粉砂岩的动态损伤力学模型，得到相应的损伤演化规律，为类似工程的建设提供一定的理论依据。

1 含水状态下泥质粉砂岩冲击试验

1.1 SHPB试验装置及试件制作

本文动态冲击试验采用Φ74mm直锥变截面SHPB装置，该试验装置主要由动力系统、弹性杆件、阻尼器、电阻应变仪和动态测试分析仪组成，试验系统满足一维平面应力条件的假定，入射杆和透射杆材质为钢材，压杆的密度为ρ1＝7 800kg/m3，波速为C1＝5 124m/s，弹性模量为E0＝210GPa。

本次试验从三峡库区采集弱风化块状泥质粉砂岩，为了尽可能保持样品的天然含水量，避免样品暴露于空气中而发生风化影响，样品表面采用多层食品保鲜膜包裹。为减少样品在运输途中可能发生的损坏，将岩石样品存放于制作牢固的木箱内，并用塑料膜密实地填充到样品四周，使岩石样品与木箱之间无空隙，装车运送至土工试验室。

然后采用钻芯机取圆柱体长条形试件，再在岩石切割机上切割成型，最后在岩石磨平机上打磨，制成标准圆柱形试件，为了满足SHPB的两个基本假定，试验的试件高度不宜过大，制作好的标准圆形试件进行加工，用岩石切割机切割成高度约为38mm的圆柱形试件，试件样品见图1。

图1 泥质粉砂岩试样Fig.1 Argillaceous siltstone specimens

1.2 SHPB试验阶段

本文分别对3种不同含水状态的泥质粉砂岩进行SHPB动态力学性能测试。对于岩石含水率的控制，编号9-1、9-2岩样的含水率为天然含水率，以下简称为天然含水状态；编号8-1、8-2岩样的含水率为在大气压力和室温条件下自由吸入水的质量与岩样干质量之比，称为吸水率，以下简称为自然吸水状态；编号7-1、7-2岩样的含水率为在经过12h煮沸后得到的饱和吸水率，以下简称为饱水状态。测试完毕后，迅速进行冲击试验。SHPB动态冲击试验的过程如图2所示。

图2 SHPB动态试验冲击过程Fig.2 The dynamic impact process of SHPB test

图3为泥质粉砂岩在不同含水状态下实测的动态应力—应变曲线，其中（a）为冲击速度为14.51 m/s时的应力—应变关系曲线，（b）为冲击速度为18.80m/s时的应力—应变关系曲线。

图3 泥质粉砂岩不同含水状态下的应力—应变关系曲线Fig.3 The stress-strain curve of argillaceous siltstone under different moisture states

由图3可知，试件在冲击荷载作用下裂纹源的出现和发展说明局部呈现出脆性断裂特征，对于动态应力-应变曲线也可以采用类似准静态单轴压缩试验中的划分方式，只不过由于动态压缩试验冲击过程时间很短，岩石为脆性材料，试件内部的裂纹源来不及完全闭合，所以准静态下的孔隙裂隙压密阶段在动态应力-应变曲线上表现得不显著，试件将很快进入弹性变形阶段。因此，可以将岩石动态应力—应变曲线划分为3个阶段，即弹性变形至微破裂稳定发展阶段、非稳定破裂发展阶段及破坏后阶段。

由图3（a）可知，在同一冲击速度下，天然含水状态和自然吸水状态的应力—应变曲线较为接近，初始阶段呈现出明显的线弹性变形特征，随后进入非稳定破裂发展阶段，当应力达到约为285MPa时，试件进入破坏后阶段；饱水状态的曲线变化较大，有明显的弱化现象，当应力达到215MPa时，试件就进入破坏后阶段，试件的峰值强度随着含水率的增大逐渐减小。图3（b）也反映了类似的规律，说明含水状态的变化对岩石的动态力学性能影响较大，尤其是饱水过程使试件的强度明显降低。

比较图3（a）和（b）可知，在同一含水状态下，加载速率越大试件的峰值强度越高，即试件的破坏强度随着加载速率的增加而增大；加载速率越大，试件的变形越大，即试件的变形随着加载速率的增加而增大。

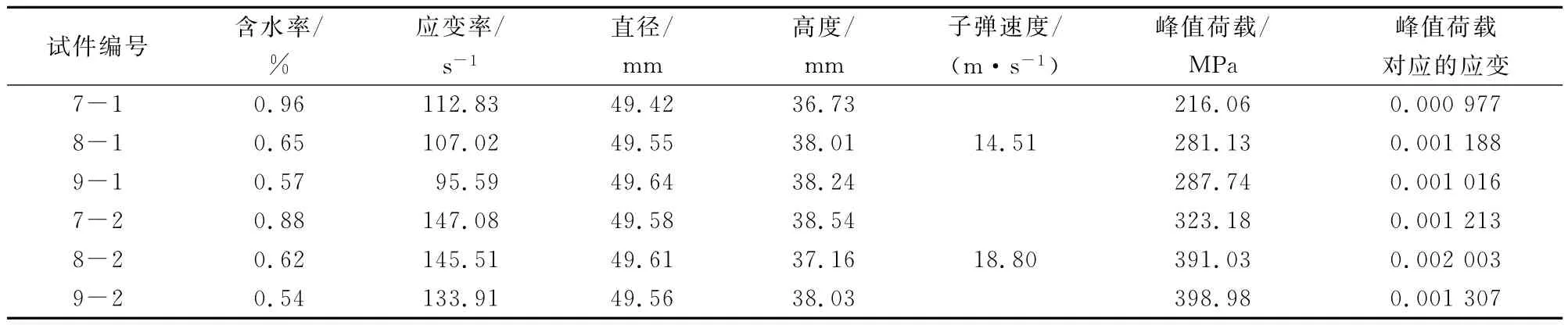
表1 泥质粉砂岩的试验参数及试验结果Table 1 The test parameters and results of argillaceous siltstone

表1为泥质粉砂岩的试验基本参数及在动载作用下的试验结果。由表1可知，试件的应变率随着子弹速度的增大而呈现增加的趋势；加载速率为14.51m/s时，天然含水状态和自然吸水状态试件的峰值强度较为接近，约为285MPa，饱水状态试件的峰值强度明显降低，约为216MPa，峰值荷载所对应的应变较为接近，约为0.001；加载速率为18.80 m/s时，天然含水状态和自然吸水状态试件的峰值强度也较为接近，约为385MPa，饱水状态试件的峰值强度明显降低，约为323MPa，峰值荷载所对应的应变较为接近，约为0.001 5。天然含水状态和自然吸水状态下的试件峰值强度较接近，主要原因是试件的大开孔隙均较小，两状态的含水率较为接近。

2 泥质粉砂岩的动态损伤本构模型

在建立本构模型的过程中，可将连续损伤理论和统计强度理论结合起来［10］。本文将考虑采用时效损伤模型来建立泥质粉砂岩的力学模型。

2.1 考虑岩石破坏准则

损伤变量与岩石微元强度有关［11］，为了体现复杂应力状态对岩石强度的影响，有必要考虑岩石的破坏准则，岩石的强度破坏理论主要有库仑强度准则、摩尔强度理论、Griffith强度准则和Druckre-Prager准则。考虑几种准则的优缺点，综合考虑，选择Druckre-Prager准则，可设基于Druckre-Prager准则的岩石微元强度为［11-13］：

式中：F—微元体强度的分布变量；a0＝sinφ/φ—岩石的内摩擦角；I1—应力张量的第一不变量；J2—应力偏量的第二不变量。

结合弹塑性力学的理论知识，在一维应力状态下，σ2＝σ3＝0，ε1＝ε，故可将岩石微元体强度的表达式变为［9］：

式中：E—弹性模量；ε—应变。

并且各微元体中的损伤体的强度服从Weibull分布，且在基于统计学理论，得到满足Weibull分布的统计损伤变量［11］。

式中：F—微元体强度的分布变量；m及F0为Weibull分布的统计损伤变量。

2.2 本构模型的建立

如图4所示，模型是由两个元件组成的并联体，假设泥质粉砂岩同时具有统计损伤特性和黏性液体特性，可以把泥质粉砂岩看成损伤体Da和黏缸ηb的并联体。根据岩石力学中的定义，可知组合体的应变等于两个分体的应变；组合体的应力等于两个分体的应力之和，即：

式中：ε—组合体的应变；εa—损伤体Da的应变；εb—黏缸ηb的应变；σ—组合体的应力；σa—损伤体Da的应力；σb—黏缸ηb的应力。

再将损伤体与黏性体的本构关系代入（4），并根据等效应变假设［14］，即可得到泥质粉砂岩的本构模型：

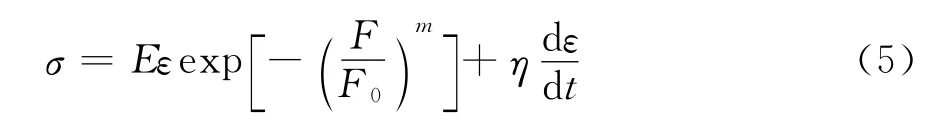
式中：η—动力黏滞系数；—应变率。

η，φ对模型参数拟合的计算影响非常小。因此参考相关文献［13，15］，粗略估计一组较为合理的参数值。

图4 时效损伤模型Fig.4 The time dependent damage model

2.3 泥质粉砂岩模型参数的辨识

结合上述所建立的损伤本构方程，对本文泥质粉砂岩试件进行拟合，通过数据进行试算分析，确定出试件本构模型的拟合参数。拟合的参数如表2所示。理论计算结果与试验测试结果对比如图5所示。

表2 各含水状态下泥质粉砂岩试件的拟合参数Table 2 The fitting parameters of argillaceous siltstone under different moisture states

从表2中可以看出，损伤参数F0与弹性模量有一定的相关性，弹性模量越大，损伤参数F0也越大；且与冲击速度也有一定的相关性，在饱水和天然含水状态下，损伤参数F0随冲击速度增大呈现出一定的递增趋势。

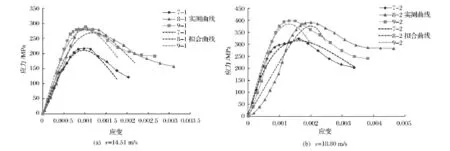
图5 不同含水状态岩样的实测与理论结果对比曲线Fig.5 The correlation curves of measured and theoretical results under different moisture states

如图5所示为动态时效损伤模型理论计算结果与实测结果的对比，其中实线表示实测曲线，虚线表示拟合曲线。从图中可以看出，试验的实测曲线与本构模型的拟合曲线具有较好的一致性，能够在一定程度上反映试件强度与应变、应变率之间的关系，验证了该模型对描述泥质粉砂岩冲击动力特性的适用性。

当冲击速度为14.51m/s，应变率较低时，曲线的一致性较高；当冲击速度增大到18.80m/s，应变率增加时，两曲线间的差异存在一定波动。但是从总体模拟的本构曲线来看，该模型是有效的，且应变率越低，模拟的效果越好，该模型在总体上很好地模拟了泥质粉砂岩的冲击破坏特性。

2.4 不同含水率泥质粉砂岩的损伤演化规律

由动态统计损伤模型的建立过程及损伤力学理论知识可知，损伤变量D是应变ε的函数，同时由式（3）可知，损伤变量D是与微元体强度及Weibull分布的统计损伤变量有关的函数，故可求得损伤变量D随应变的变化规律，如图6所示。

图6 冲击加载过程损伤演化规律Fig.6 The damage evolution law under impact load

由图6可知，损伤变量D随着应变的增加呈现出逐渐增大的趋势，在弹性变形至微破裂稳定发展阶段，损伤值很小，且增加速率缓慢，在应力应变达到峰值时，损伤值急剧增大，且当应变达到最大时，损伤值也达到最大，接近于1.0。

当冲击速度为14.51m/s时，不同含水率的损伤变量D随应变的变化规律较为一致，但是饱水状态试件的曲线斜率都略大于天然含水状态和自然吸水状态，说明饱水状态试件的损伤值的变化速率大于天然含水和自然吸水状态，且达到峰值应变后，饱水状态试件的损伤值超过天然含水和自然吸水状态；当冲击速度为18.80m/s时，在相同应变情况下，饱水状态试件的损伤值都大于天然含水和自然吸水状态，且由于冲击速度较大，试件内部的裂纹源来不及完全闭合，很快进入弹性变形阶段，损伤值的变化速率没有较明显的变化规律，饱水状态和自然吸水状态下的曲线较天然含水状态下的差异较大，这可能是由于加载速率的增大及岩样内部差异造成的。但是，总体来说，饱水状态下损伤值的变化最大，饱水过程造成试件的微裂隙源增加，导致损伤加大。

3 结论

本文利用SHPB装置对泥质粉砂岩进行了不同含水状态及不同冲击速度下的动态力学性能试验，并基于连续损伤理论和统计强度理论建立力学模型，进行模型的拟合，主要得到以下几个结论：

1）含水状态的变化对岩石的动态力学性能有较大影响，试件的强度随着含水率的增加而逐渐减小，尤其是饱水过程使试件的强度明显降低。不同含水率情况下，试件的峰值强度及变形随着加载增加而逐渐增大。

2）从拟合参数的结果可以发现，损伤参数F0与弹性模量及冲击速度有一定的相关性，弹性模量越大，损伤参数F0也越大；在饱水和天然含水状态下，损伤参数F0随冲击速度增大呈现出一定的递增趋势。

3）应变速率较低时，试件的拟合曲线和实测曲线的一致性较高；应变率增加时，试件的拟合曲线和实测曲线波动较大。但从本构模型的理论计算结果来看，该模型在总体上很好地模拟了泥质粉砂岩的冲击破坏特性。

4）损伤变量D随着应变的增加呈现出逐渐增大的趋势，在弹性变形至微破裂稳定发展阶段，损伤值很小，且增加缓慢，在应力应变达到峰值时，损伤值急剧增大，且当应变达到最大时，损伤值也达到最大，接近1.0。饱水状态下损伤值的变化最大，饱水过程造成试件的微裂隙源增加，导致损伤加大。

［1］蒋关鲁，房立凤，王智猛，等.红层泥岩路基填料动强度和累积变形特性试验研究［J］.岩土工程学报，2010，32（1）：124-129.

［2］孔祥辉，蒋关鲁，邹祖银，等.循环荷载下红层泥岩的动力特性及路用性能研究［J］.岩石力学与工程学报，2013，32（9）：1813-1819.

［3］钟冬望，吴 亮，陈 浩.爆炸荷载下岩质边坡动力特性试验及数值分析研究［J］.岩石力学与工程学报，2010，29（增刊1）：2964-2971.

［4］王祥秋，杨林德，高文华.复杂围岩隧道洞口段动力响应特性分析［J］.岩石力学与工程学报，2005，24（24）：4461-4465.

［5］杨圣奇，徐卫亚，苏承东.考虑尺寸效应的岩石损伤统计本构模型研究［J］.岩石力学与工程学报，2005，24（24）：4484-4490.

［6］翟 越，赵均海，李寻昌，等.岩石类材料损伤黏弹塑性动态本构模型研究［J］.岩石力学与工程学报，2011，30（增刊2）：3820-3824.

［7］郑永来，夏颂佑.岩石粘弹性连续损伤本构模型［J］.岩石力学与工程学报，1996，15（增刊1）：428-432.

［8］谢理想，赵光明，孟祥瑞.岩石在冲击载荷下的过应力本构模型研究［J］.岩石力学与工程学报，2013，32（增刊1）：2772-2781.

［9］朱晶晶，李夕兵，宫凤强，等.单轴循环冲击下岩石的动力学特性及其损伤模型研究［J］.岩土工程学报，2013，35（3）：531-539.

［10］KRAJCINOVIC D，SILVA M A G.Statistical aspects of the continuous damage theory［J］.International Journal of Solids and Structures，1982，18（7）：551-562.

［11］曹文贵，赵明华，刘成学.基于Weibull分布的岩石损伤软化模型及其修正方法研究［J］.岩石力学与工程学报，2004，23（19）：3226-3231.

［12］单仁亮，薛友松，张 倩.岩石动态破坏的时效损伤本构模型［J］.岩石力学与工程学报，2003，22（11）：1771-1776.

［13］耶格J C，库克N G C.岩石力学基础［M］.北京：科学出版社，1983.

［14］Lemaitre J.An equivalent strain hypothesis［J］.J.Engng，Materials and Technology，1985，107（1）：83-89.

［15］刘佑荣，唐辉明.岩体力学 ［M］.北京：中国地质大学出版社，1999.

Study on the damage feature of water-bearing argillaceous siltstone under the impact load

ZHAN Jinwu1，ZHANG Naiyang2，HUANG Ming2，ZHANG Bingqi2
（1.School of Civil Engineering，Beijing Jiaotong University，Beijing 100044，China；2.College of Civil Engineering，Fuzhou University，Fuzhou 350108，China）

By using the Split Hopkinson Pressure Bar（SHPB），the test for the dynamic mechanics properties of the argillaceous siltstone with different water contents are presented，and the influence of the moisture content on them is also analyzed.The dynamic damage model of argillaceous siltstone is established on the basis of the continuum damage theory and statistical strength theory，and the corresponding damage evolution rule is also obtained.It shows that the curve fitted by the constitutive model established by the Weibull distribution has a good consistency with the testing curve.The damage parameterF0has a certain correlation with the elastic modulus and impact velocity.The bigger the elasticity modulus，the greater the damage parameterF0will be.What’s more，the change of moisture content has great influence on the dynamic characteristics of rock.

SHPB；argillaceous siltstone；impact speed；moisture state；damage model

TU452；TD315

Α

1671-4172（2015）06-0044-05

国家自然科学基金资助项目（41202195）

詹金武（1989-），男，博士研究生，主要研究方向为岩土与地下工程。

黄 明（1983-），男，副教授，博士，主要研究方向为岩土与地下工程。

10.3969/j.issn.1671-4172.2015.06.009