掘进巷道压入式通风粉尘运移规律数值模拟

龚剑，胡乃联，林荣汉，崔翔

(北京科技大学金属矿山高效开采与安全教育部重点实验室，北京100083)

掘进巷道压入式通风粉尘运移规律数值模拟

龚剑，胡乃联，林荣汉，崔翔

(北京科技大学金属矿山高效开采与安全教育部重点实验室，北京100083)

为了解决掘进巷道粉尘的严重污染问题，以西藏自治区某铜多金属矿为工程背景，运用数值模拟与现场测试相结合的方法，对掘进巷道采用压入式通风时的粉尘分布规律进行研究。通过GAMBIT建立几何模型，并运用FLUENT软件模拟压入式通风条件下粉尘的运移规律。模拟结果表明，掘进巷道内的粉尘在1 200 s时基本全部排出，同时模拟结果与实测数据基本一致。

掘进巷道;压入式通风;粉尘分布;数值模拟

掘进工作面在钻孔、爆破及装岩过程中都会产生粉尘，是井下生产作业产尘量最大的尘源之一，同时由于独头巷道通风距离长，通风条件差，粉尘不易排出，致使粉尘大量分布于掘进巷道内，对人体危害极大［1－4］。各工种尘肺病的患病率调查数据显示，掘进工人尘肺病患病率最高，因而必须对掘进巷道的粉尘治理予以重视［5］。基于此，本文以西藏自治区某铜多金属矿为工程背景，根据气固两相流理论，采用GAMBIT建立掘进巷道内压入式通风粉尘运移规律数学模型，同时利用FLUENT研究压入式通风过程中粉尘的运动轨迹与浓度变化规律，并将现场实测数据与模拟结果进行对比，验证数值模拟的准确性。

1 工程背景

西藏自治区某铜多金属矿地下开采方式为斜坡道开拓，倾角为8°，总长800 m，巷道断面为三心拱，宽4.2 m，高3.7 m，在4 470 m中段存在大量的掘进断面，风流不能形成回路，导致通风不畅，粉尘不能及时有效排出。另外矿石与废石的提升运输只能利用矿车来实现，矿车发动机为柴油驱动，需要耗费大量的氧气，当氧气供应不足时，尾气的排放量成倍增加，尾气排放量增加带来的直接危害就是空气中细颗粒物浓度的增大。因此，一方面4 470 m中段掘进工作面由于独头巷道通风不畅而导致粉尘分布集中，另一方面尾气的大量排放致使粉尘浓度明显增大，二者的共同作用导致掘进巷道粉尘污染十分严重。

2 几何模型的建立及求解

2.1 模型选定

粉尘在空气中的运动规律可运用气固两相流理论进行研究，通常采用欧拉-拉格朗日法将气体看作背景流体，将粉尘看作离散分布于空气中的颗粒，运用气体流动控制方程组，采用非稳态不可压Navier-Stokes方程和工程上应用最广的k-ε双方程模型求解［6］，方程组可表示为:

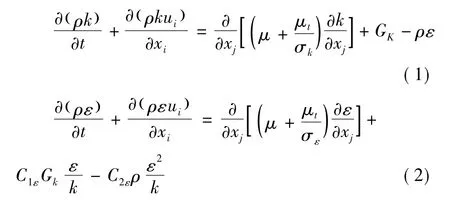
式中:Gk-湍动能变率，k表示湍动能，m2/s2; ε-湍动能耗散率，m2/s2;μ-层流黏性系数，Pa·s; μt-湍流黏性系数，Pa·s;ρ-气体密度，kg/m3;ui-流体在X方向上的速度，m/s;C1ε、C2ε、Cμ、σk和σε分别取1.44、1.92、0.09、1.00和1.30。

2.2 模型假设

由于4 470 m掘进巷道现场情况较为复杂，若将所有因素全部考虑，不利于模型的建立与网格的划分，因此需要对掘进巷道粉尘分布计算域做出以下假设:

1)掘进巷道内电缆电线、水管等杂物由于对粉尘沉降影响不大，模型中不予考虑。

2)掘进巷道为标准三心拱巷道，巷道断面始终保持一致。

3)压入式风筒是采场内通风除尘设计的重要组成部分，建模中考虑在内。

4)掘进断面爆破粉尘全部产生于实施爆破阶段，不考虑爆破准备阶段及爆破后转运时产生的粉尘。

5)掘进巷道模型内只考虑动量传输，忽略热传导。

2.3 模型建立

基于上述假设，根据4 470 m掘进巷道的实际情况对其内部几何条件合理简化，使用GAMBIT建立掘进巷道的几何模型并划分网格，掘进巷道尺寸为50 m(长)×4.2 m(宽)×3.7 m(高)，顶部为三心拱构造，压入式风筒直径为0.5 m，出风口距工作面12 m，风筒中心距地面2.3 m，如图1所示。

2.4 边界条件

在GAMBIT中将几何模型及网格划分完成后，导入FLUENT中进一步设置求解类型以及边界条件等参数［7－10］。为了描述粉尘颗粒的运动轨迹，气相流场使用湍流模型，采用SIMPLI算法进行计算，颗粒的轨迹跟踪则由离散相模型(DPM模型)完成。数值模拟参数及边界条件的设定如表1所示。

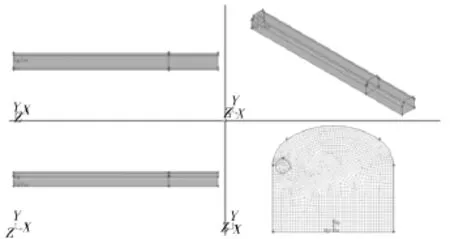
图1 掘进巷道几何模型Fig.1 Geometric model of the excavation roadway

表1 计算模型参数设定Table 1 Definingmodel parameters

3 数值模拟结果及分析

3.1 粉尘运动轨迹

将已完成网格划分的模型导入FLUENT中并进行边界条件设置，经过迭代计算后，得到掘进巷道内风流速度流线图，如图2所示。根据圆形贴附射流理论，掘进工作面压入式通风可以认为是末端封闭的受限圆形贴附射流通风［11－12］，由图2可以看出，风流起始按贴附射流规律发展，而受独头巷道空间限制，使得在迎头处射流向相反方向流动，在独头巷道工作区分别形成了射流区和回流区，又由于射流的卷吸作用在射流区和回流区界面上同时形成了涡流区。射流区风速由风筒出口到掘进面不断减小，风筒出口风速为12.74 m/s，到达距离掘进面1 m处风速降低到5 m/s，到掘进面时风速为1.2 m/s，射流区风速降低较快。回流区风速由掘进面到出口先增大后持续减小，从掘进面到距工作面5 m处，风速增大到3 m/s，随后持续减小，距工作面10 m处风速为2 m/s，到达距离工作面20 m处风速降低到1 m/ s，到达距工作面40 m处风速降低为0.22 m/s。

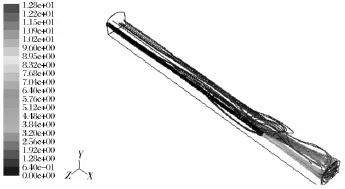
图2 掘进巷道风流流线图Fig.2 Airflow line in excavation roadway

图3所示为掘进巷道粉尘分布轨迹的数值模拟结果。从图中可以看出，粉尘粒径大于20 μm的颗粒都沉积下来，含尘风流以微细颗粒粉尘为主，且大颗粒粉尘基本在远离掘进面处沉积，这是由于远离掘进面处风流速度降低，颗粒的重力作用超过风流对颗粒的拖曳力作用。而粒径更为细小的粉尘绝大部分漂浮在巷道风流中，重力对微细颗粒的作用不明显，粒径分布无明显规律。

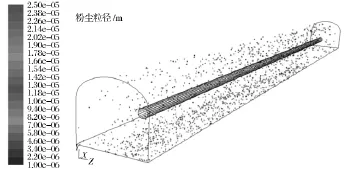
图3 掘进巷道粉尘粒径分布轨迹图Fig.3 Dust distribution in excavation roadway

3.2 粉尘浓度变化规律

采用压入式通风时，掘进巷道内粉尘的浓度变化规律如图4、5所示。图4表示粉尘的沿程变化规律，图5表示粉尘的垂直变化规律。从图中可以看出:

图4 掘进巷道不同位置粉尘浓度变化规律Fig.4 Variation of dust concentration at different locations in excavation roadway

图5 掘进巷道不同高度粉尘浓度变化规律Fig.5 Variation of dust concentration at different heights in excavation roadway

1)在60～300 s时间内，粉尘在风流回流作用下，逐渐远离掘进面，粉尘浓度下降幅度较为明显; 300～1 200 s时间内，粉尘质量浓度下降缓慢，其中大部分是粒径细小的粉尘，受空气浮力及风流速度的影响，在空气中沉降的速度较慢。掘进巷道内的粉尘在1 200 s时基本全部排出，除尘效果较好。

2)随着时间推移，粉尘质量浓度最大值逐步向巷道出口移动，且数值呈逐步降低趋势，但在5～20 m区域，粉尘浓度小幅上升，这是由于风流速度在距离掘进面5 m处下降，导致粉尘移动变慢，粉尘重新聚集，粉尘质量浓度再次升高;而在距离掘进面20 m后，风速稳定，从而粉尘浓度保持递减趋势。

3)随着时间推移，巷道内不同垂直高度的粉尘浓度总体随高度下降而升高。100 s前，由于大颗粒粉尘的沉降作用，2 m和1.5 m的粉尘浓度不同程度下降，而1 m和0.5 m的粉尘浓度不同程度升高。100～300 s时间内，各个高度粉尘浓度保持缓慢降低趋势;300 s后，各垂直高度粉尘浓度迅速降低。

4 现场实测数据对比分析

根据现场实际条件，选取距离掘进工作面5 m处布置采样点，采用多通道激光尘埃粒子计数器对采场爆破后粉尘质量浓度进行监测。实际的监测结果与数值模拟结果对比图如图6所示。图6所示的模拟结果与实测结果的走势基本相符，由此可知数值模拟出的粉尘浓度变化规律与实际情况基本吻合，但在粉尘浓度最大值以及部分时间段存在偏差，出现偏差主要是因为数值模型简化了现场条件，数值模拟结果不能完全等同于实际情况。通过与现场实测数据的对比分析，可得出数值模拟结果是基本准确的，说明了离散相模型对粉尘质量浓度分布与变化规律的适用性。

5 结论

1)压入式通风的风流由于射流的卷吸作用会形成涡流区域，风速损失较大，距工作面40 m处风速已基本降低至零。风速的降低会引起粉尘粒径大于20 μm颗粒的沉积，含尘风流主要以微细颗粒粉尘为主。

2)压入式通风时，粉尘浓度的数值随着时间的推移逐步降低，但由于风速的不稳定会导致粉尘浓度小幅波动。掘进巷道内的粉尘在1 200 s时基本全部排出，除尘效果较好。

3)由于数值模型进行了简化，与实测数据存在一定偏差，但总体上数值模拟结果与实测数据基本相符，说明运用欧拉-拉格朗日法对掘进巷道的粉尘分布规律进行数值模拟是可行的。

［1］刘毅，蒋仲安，蔡卫，等.综采工作面粉尘运动规律的数值模拟［J］.北京科技大学学报，2007，29(4):351－353.

［2］时训先，蒋仲安，周姝嫣，等.综采工作面粉尘分布规律的实验研究［J］.煤炭学报，2008，33(10):1117－1121.

［3］陈举师，蒋仲安，杨 斌，等.破碎硐室粉尘浓度空间分布规律的数值模拟［J］.煤炭学报，2012，37(11):1865－1870.

［4］蒋仲安，陈举师，牛 伟，等.皮带运输巷道粉尘质量浓度分布规律的数值模拟［J］.北京科技大学学报，2012，34(9):977－981.

［5］杜翠凤，王 辉，蒋仲安，等.长压短抽式通风综掘工作面粉尘分布规律的数值模拟［J］.北京科技大学学报，2010，32(8): 957－962.

［6］谢振华，宋存义.工程流体力学［M］.北京:冶金工业出版社，2009.

［7］杨胜来.综采工作面粉尘运移和粉尘质量浓度三维分布的数值模拟研究［J］.中国安全科学学报，2001，11(4):61－64.

［8］陈举师，王毅，蒋仲安.采场爆破烟尘浓度分布及扩散规律的数值模拟［J］.煤炭学报，2013，38(4):147－152.

［9］秦跃平，张苗苗，崔丽洁，等.综掘工作面粉尘运移的数值模拟及压风分流降尘方式研究［J］.北京科技大学学报，2011，33 (7):790－794.

［10］姚玉静，程卫民，聂文，等.综掘工作面粉尘质量浓度分布的数值模拟［J］.矿业安全与环保，2011，38(3):21－24.

［11］王海桥，施式亮，刘荣华，等.压入式受限贴附射流流场特征及参数计算［J］.黑龙江科技学院学报，2001，11(4):4－7.

［12］邓国祥.压入式通风施工隧道内空气流动方向和速度研究［J］.铁道劳动安全与卫生环保，1997，24(4):263－265.

Numerical simulation on dust migration law in excavation roadway with forced ventilation

GONG Jian，HU Nailian，LIN Ronghan，CUI Xiang
(State Key Laboratory of High-Efficient Mining and Safety of Metal Mines，Ministry of Education，USTB，Beijing 100083，China)

In order to solve the problem of severe dust pollution in excavation roadway，the dust distribution in excavation roadway with forced ventilation is studied by the combined method of numerical simulation and on site measurements in a poly-metallic ore in Tibet autonomous region as the engineering background，the geometric model is established through GAMBIT and dust distribution with forced ventilation is simulated with the computational fluid dynamics software FLUENT.The simulation results indicate that the dust in excavation roadway is almost completely ejected at the time of 1 200 s，which are essentially coincident with the measured data.

excavation roadway;forced ventilation;dust distribution;numerical simulation

TD72

Α

1671-4172(2015)01-0065-04

"十二五"国家科技支撑计划项目(2012BAB01B04);长江学者和创新团队发展计划资助项目(IRT0950)

龚剑(1987－)，男，博士研究生，采矿工程专业，主要从事矿山安全保障技术方面的研究。

10.3969/j.issn.1671-4172.2015.01.015