统计地震学在矿山动力灾害预测中的应用

李京濂，尚仕科，张 君，张 达

(1.中矿金业股份有限公司，山东招远265400;2.北京矿冶研究总院，北京102628)

统计地震学在矿山动力灾害预测中的应用

李京濂1，尚仕科1，张 君2，张 达2

(1.中矿金业股份有限公司，山东招远265400;2.北京矿冶研究总院，北京102628)

许多观测资料表明矿山微震事件同天然地震事件都服从古登堡-里克特关系。矿山动力灾害事件实际上是矿山岩体系统的一种自我调整，运用统计地震学研究微震事件集的演化规律，以揭示岩体所处的稳定性阶段，从而对危险性岩体动力灾害事件做出预测。结合玲南金矿的微震监测数据，运用古登堡-里克特关系研究该矿山连续三个月的b值变化趋势、微震事件震级重现周期和对应事件的发生概率。结果表明，b值基本能反映当月的矿山系统稳定性情况，并能给出相应震级事件重现周期和发生概率。

统计地震学;古登堡-里克特关系;b值;预测

地震学和其它学科一样，可以使用统计工具进行统计分析、统计推断、统计预测、统计检验。因此，如果把统计学在地震学中的应用作为广义的统计地震学，那么统计地震学的历史甚至可以追溯到现代地震学产生以前。二战以后，统计学的知识和工具大量应用于天然地震和工程地震问题的研究。1954年，古登堡和里克特，首先提出使用震级－频度的经验公式来描述世界各地区地震活动性的差异，从而开启了统计学在地震中的应用浪潮［1］。McGarr，Gibowicz等学者研究发现天然地震与人工诱导地震之间不存在系统的差异，因此可将天然地震理论引入到矿山地震的研究中［2］。吴忠良还专门就目前统计地震学存在的问题进行了相关论述，认为地震的预测离不开统计地震学［3］。

矿山岩体系统具有自组织临界［4］(self-organized criticality)特性，岩体在不断的人工开挖扰动下，总是从一个亚稳定状态变换到另外一个亚稳定状态，在这个变化过程中，通过岩体变形、破坏、释放能量，到达一种自我调整。矿山动力灾害事件的发生存在一个孕育过程，在孕育到最后动力灾害发生期间，微震事件的发生数量、大小、空间分布特征等参数存在一个同岩体状态耦合变化的过程，从而可以通过研究参数的变化趋势，发现岩体破坏的前兆特征，进而进行灾害预测［5－6］。本文就是基于以上思路，结合中矿金业股份有限公司玲南金矿承担的国家科技攻关项目期间所建设的深井岩爆微震监测系统的现场数据，运用统计地震学对这些数据进行动力灾害预测研究。

1 古登堡-里克特关系

许多观测资料表明，由开采诱发的地震事件与天然地震遵循同样的规则，即使矿山地震事件不是严格意义上的随机事件，但是二者都同时遵循古登堡-里克特关系［7］。

式(1)中n是震级为m的地震数目，a、b为参数。如果n为在一给定时间段内震级大于或者等于m的地震事件个数，那么式(1)可以解释为累积关系式;如果n为震级值确定在m左右小区间内的地震数目，那么式(1)又可解释为地震密度定律。参数a为地震活动性水平量度，而参数b通常接近于1，描述了在给定时间内小震个数与大震个数的相对数，如果a、b值确定，那么开采中的关系就可有章可循。例如McGarr在1984年研究南非East Rand金矿区中的一个开采区，在100 d的周期内，包括平均每天掘进约20～30 cm的近300 m的工作面区域上，古登堡-里克特公式中的参数a、b分别为2.19和0.63，假如，取ML=2.0为矿山地震可能引起破坏的最小震级，那么由古登堡-里克特关系式得出，每100 d将发生8次或9次由开采作业引起的矿山地震破坏作用。

有大量文献资料研究频度-震级关系［8－9］，结果均表明，在所有的时间和所有的地区，古登堡-里克特关系适用于所有的震级范围，但是在高震级范围内不满足这个关系，因此有些地震专家提出最大震级的概念，或者对式(1)进行修正。国内相关学者和研究人员［10－12］通过对岩石实验声发射序列处理结果和华北地区部分中强地震的拟合优度计算震例，得出岩石破坏前一定时期，声发射能量与频次不完全服从古登堡-里克特关系式，表明震级频次偏离古登堡-里克特关系式具有一定的破坏前兆意义，华北地区部分强地震在孕震过程中，在震前某一段时间内震源区及其附近地区，中小地震的发生在震级频次结构上不服从古登堡-里克特关系，这种偏离包含着一定的强地震孕育信息。

2 古登堡-里克特关系的应用

2.1 监测区域及微震事件概况

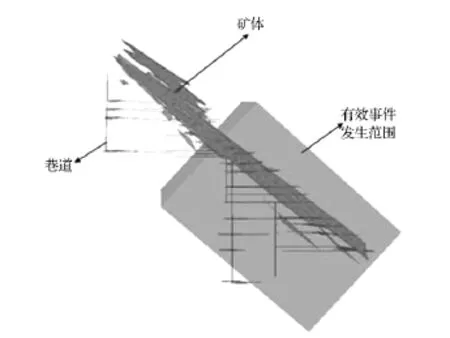
图1 玲南金矿微震监测系统有效监测区域Fig.1 The effective monitoring area of micro-seismic monitoring system in Lingnan Gold Mine

图1给出了玲南金矿微震监测系统有效的监测区域，长宽高为1 000 m×600 m ×500 m，倾角49°，单个传感器的有效监测范围是250 m，根据传感器网络布置范围，确定了以上的有效事件监测区域。

表1为2013年7、8、9三个月的微震事件统计表，包括本月发生的微震事件数量和事件震级范围。图2给出了三个月微震事件的空间分布状态，其中球体的颜色表示不同时间发生的微震事件，球体的大小表示了不同震级的微震事件。

表1 微震事件统计表Table 1 Statistics table of micro-seismic events

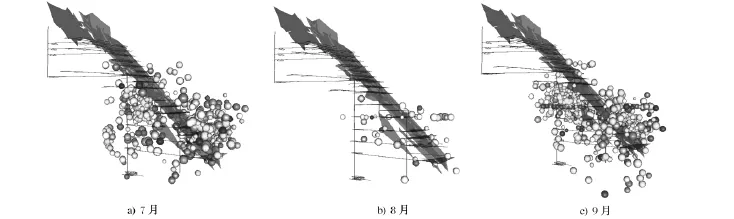
图2 玲南金矿7、8、9月微震事件空间分布特征Fig.2 Distribution of micro-seismic events in July，August and September

2.2 b值变化趋势

通过图3、4、5中事件与震级分布的关系可以看出，前半部分线性特性并不是很强，而后半部分则近乎为一条直线，其斜率的负数即为幂指数。基本上小事件比大事件数量多，但小事件和大事件的发生都起因于同一种机制。图中震级与事件频次的关系表明震级与其相应的发生频率之间存在幂律关系，具有自组织临界状态的特点。

如图3、4、5所示，横坐标表示震级，左侧纵坐标表示累计事件数，右侧纵坐标表示微震事件重现周期，微震事件震级与其出现概率成反比，震级越小出现概率越高。图中直线斜率的负数一般称为b值，b值的变化反映微震事件集合内部结构的调整，表现为大震与小震数目比例关系的变化。可以这样狭义的理解:b值减小表示微震群体内大震数目的增加，反之则减少。另外，很多研究结果表明，地震前的b值比余震的低，因此b值也可以作为识别前震的一种标志。

图3 监测区域内微震事件震级-频率分布图(2013年7月1日至7月31日)Fig.3 Magnitude-frequency distribution of micro-seismic events in July，2013

图3、4、5分别表示了2013年7、8、9三个月的微震事件的震级-频率分布图，其中矿山在7月上旬因为当地出现了长时间的暴雨导致尾矿库积水过多，风险很大，因此矿山抽调了很多技术人员进行抗洪抢险工作，导致矿山井下停止了生产;8月份系统的时间同步功能出现故障导致了很多事件无法拾取定位，因此8月份的事件相对较少，9月份修复了几个损毁的传感器电缆线，使得参与定位的传感器数目增多，同时9月份，矿山也加大了生产力度，因此可以看出9月份的事件偏多，b值也相对减小。

图4 监测区域内微震事件震级-频率分布图(2013年8月1日至8月26日)Fig.4 Magnitude-frequency distribution of micro-seismic events in August，2013

图5 监测区域内微震事件震级-频率分布图(2013年9月1日至9月30日)Fig.5 Magnitude-frequency distribution of micro-seismic events in September，2013

图6 监测区域内微震事件集b值变化曲线Fig.6 The b value trend of micro-seismic events in monitoring area

2.3 微震事件震级重现期与发生概率

表2 微震事件震级重现期(天)和发生概率(2013年7月)Table 2 Micro-seismic events recurrence interval and probability in July

表3 微震事件震级重现期(天)和发生概率(2013年8月)Table 3 Micro-seismic events recurrence interval and probability in August

表4 微震事件震级重现期和发生概率(2013年9月)Table 4 Micro-seismic events recurrence interval and probability in September

表2、3、4给出了2013年7、8、9三个月的微震事件相应震级的重现期和发生概率，表2系统软件计算的最大震级－0.1再次出现的周期是30 d，一个月内再次发生的概率是56.6%，两个月内再次发生的概率是81.1%，三个月内再次发生的概率是91.8%，四个月内再次发生的概率是99.4%，一年内再次发生的概率是100%。同理，表3给出了最大震级－0.3再次出现的周期是25 d，一个月内再次发生的概率是63.4%，表4给出了最大震级0.5再次出现的周期是29 d，一个月内再次发生的概率是59.9%。表4中－0.1级地震再次出现的周期是7 d，一个月内再次发生的概率是97.3%，对比表2可以看到9月份的大事件出现的概率和数量明显增多，表4中－0.3级地震再次出现的周期是5 d，一个月内再次发生的概率是99.7%，对比表3可以看到9月份的大事件出现的概率和数量明显增多。总体上9月份出现的微震事件总数，出现大震级的微震事件的频率高于7月份和8月份，从图6监测区域内微震事件集b值变化曲线(b值选择了系统计算出的误差范围内最小值)可以看出，曲线先上升后下降，下降的幅度较上升的幅度大，b值下降意味着岩体和应力的非均匀性增加，应力上升，围岩刚度降低，矿山的安全风险增加。

3 结论

1)矿山震级与事件频次的关系表明，震级与其相应的发生频率之间存在幂律关系，具有自组织临界状态的特点。

2)b值的变化反映了微震事件集合内部结构的调整，b值减小表示微震群体内大震数目的增加，反之则减少。

3)玲南金矿7、8、9三个月对应不同的b值，基本能反映当月的矿山系统稳定性情况，b值越小意味着岩体和应力的非均匀性增加，应力上升，围岩刚度降低，矿山的安全风险增加。

4)根据古登堡-里克特关系还能估计下一周期内大震级事件或者灾害事件重现周期以及发生的概率，从而为矿山动力灾害预测提供指导。

［1］Mendecki A J.Seismic monitoring in mines［M］.London:Chapman＆Hall，1997.

［2］唐礼忠.深井矿山地震活动与岩爆监测及预测研究［D］.长沙:中南大学，2008.

［3］吴忠良，朱传镇，蒋长胜，等.统计地震学的基本问题［J］.中国地震，2008，24(3):197－206.

［4］陆菜平，窦林名，吴兴荣.冲击矿压诱因-能量积聚与耗散的自组织临界性［J］.辽宁工程技术大学学报，2005，24(6):841－843.

［5］杨承祥，罗周全，唐礼忠.基于微震监测技术的深井开采地压活动规律研究［J］.岩石力学与工程学报，2007，26(4):818－824.

［6］唐礼忠，张 君，李夕兵，等.基于定量地震学的矿山微震活动对开采速率的响应特性研究［J］.岩石力学与工程学报，2012，31(7):1349－1354.

［7］Gibowciz S J，Kijko A.矿山地震学引论［M］.修济刚，徐平，杨心平，译.北京:地震出版社，1998.

［8］帕切科，肖尔茨，赛克斯，等.小震到大震的频度-震级关系的变化［J］.国际地震动态，1992(11):11.

［9］尚仕科，张苏闯，王平，等.微震事件的多参数信息监测岩爆技术研究［J］.有色金属(矿山部分)，2014，66(6):1－3，14.

［10］路鹏，李志雄，陶本藻，等.震级频度与古登堡-里克特关系式偏离的前兆意义［J］.地震，2006，26(4):1－8.

［11］严尊国，陈俊华.地震震级-频度G-R关系的偏离度［J］.地震，1995(4):328－332.

［12］李志雄，陶本藻，PONOMAREV A V，等.震级频度与古登堡-里克特关系式偏离的实验与震例分析［J］.武汉大学学报，2009，55(6):721－727.

Application of statistical seismology in prediction of mine dynamic disaster

LI Jinglian1，SHANG Shike1，ZHANG Jun2，ZHANG Da2
(1.Zhongkuang Gold Industry Co.，Ltd.，Zhaoyuan Shandong 265400，China; 2.Beijing General Research Institute of Mining＆Metallurgy，Beijing 102628，China)

A lot of observation data show Gutenberg-Richter law can fit mine micro-seismic events like nature earthquake.In fact mine dynamic disasters is a kind of self-adjustment to mining rock mass system，which could be predicted with seismic events group researched by statistical seismology to reveal stage of stability of rock mass.In this paper the b value tendency，seismic events mean recurrence days and magnitude probability in Lingnan gold mine in three months is studied by Gutenberg-Richter law.The results show that the b value can basically response to conditions of mine system stability in a month，and seismic events mean recurrence days and magnitude probability can be given.

statistical seismology;Gutenberg-Richter law;b value;prediction

TD76

Α

1671-4172(2015)01-0007-04

“十二五”国家科技支撑计划项目(2012BAK09B03)

李京濂(1966－)，男，工程师，地质矿产勘查与勘探专业，主要从事矿山地质勘查与矿山地质和生产安全等方面的工作。

10.3969/j.issn.1671-4172.2015.01.002