D(0，3)图的Cordial 性①

倪臣敏，刘峙山，卢福良

(1.厦门工学院 高等数学教学系，福建 厦门361021;2.呼和浩特职业学院，内蒙古 呼和浩特010000;3.临沂大学 数学系，山东 临沂276000)

0 引 言

图的标号问题源于60 年代中期G.Ringel［1］和A.Rosa［2］提出的优美树的猜想，现已成为一个重要而活跃的研究分支［6～13］.相关的结果被广泛应用于射电天文学、X－射线衍射晶体学、密码设计、导弹控制码设计、同步机码设计等领域［3～4］.Cordial 标号是优美标号及调和标号的一种弱化，其研究始于1987 年Cahit 的一篇论文［5～6］，在这篇论文中，Cahit 明确给出了Cordial 图的定义.在文献［7］中，Seoud 和Abdel Maqusoud 证明了奇度图是Cordial 图的充分条件为;在文献［8］中，完善了Seoud 和Abdel Maqusoud 的结论，证明了D(1，3)图是Cordial 图的充要条件为;在文献［9］中，作者证明了3 正则图是Cordial 图的充要条件为4.在本文中，将讨论D(0，3)图的Cordial 性，并证明了所有的D(0，3)图都是Cordial 图.

本文论及的都是无向有限的简单图，标号均为0－1 标号.对于图G 的顶点集合V(G)的标号f，以导出G 的边集合E(G)的标号.以Vi=Vi(G)={v|v ∈V(G)，f(v)=i}表示所有的顶点标号为i 的点构成的集合，以Ei=Ei(G)={uv|u，v ∈V(G)，f(uv)=i}表示所有的标号为i 的边构成的集合，i=0，1.记i，f(v)=j，或f(u)=j，f(v)=i}，{i，j}={0，1}，E0=E00∪E11，E1=E01∪E10，并以v0，v1，e0，e1分别表示它们的基数.当同一图G 有更细的标号时，引入更细的记号，如用v0(f)=v0(f:G)=v0(G)表示图G 中标号f 为0 的顶点集合的基数，用e0(f)=e0(f:G)=e0(G)表示图G 中标号f 为0 的边集合的基数.文中标i 的顶点或者边简称为i 点或者i 边，其中i=0，1.其它相关专业术语可详见文献［12］.

定义1［6］若图G 存在一个0－1 标号f 满足:(1)|v0(G)－v1(G)|≤1;(2)|e0(G)－e1(G)|≤1，则称f 是G 的Cordial 标号，称G 为Cordial 图.

定义2 设dG(x)(或简写为d(x))为图G 中顶点x 的度，若对于任意x ∈V(G)，dG(x)∈{i1，…，ik}，k ∈N 则称图G 为D(i1，…，ik)图.

定义3［10］对于图G，若存在一个Cordial 标号f，使得v0(f:G)=v1(f:G)，e0(f:G)=e1(f:G)，则称G 为严格Cordial 图.

1 主要内容

引理1 设G=A ∪B，其中B 为由孤立点构成的图.若A 为Cordial 图，则G 为Cordial 图.

证明: 显然，G 中的边即为图A 的边.设f 是图A 的Cordial 标号，在G 中保持f 在A 中的顶点标号不变，则G 中A 的边标号不变;调整B 中的顶点标号，容易获得满足定义1 的Cordial 标号，故G 为Cordial 图.

引理2 在一个图中增加或者减少一个严格Cordial 图的分支，不改变图的Cordial 性

此证明略，读者可自行推导.

定理1 设G 为D(0，3)图，且每个分支的阶不大于4，则G 为Cordial 图.

证明: 由题意，G 的每个分支或者为孤立点，或者为4 阶3－正则图.容易验证两个4 阶3－正则图的并为严格Cordial 图，依次从G 中去除一对一对的4 阶3－正则图，设最后G 被化简成的图为M，则M 有两种情况.

情况1，M 由孤立点构成，则M 为Cordial 图，由引理2，G 为Cordial 图.

情况2，M 由一个4 阶3－正则图和孤立点构成.给此3－正则图如图1 的标号，若孤立点的个数为奇数个，则将孤立点标n+1 个0，n 个1，此时|v0(M)－v1(M)|=|n+1+1－(n+3)|≤1;|e0(M)－e1(M)|=0 ≤1，故M 为Cordial 图，由引理2，G 为Cordial 图;若孤立点的个数为偶数个，则将孤立点标n+1 个0，n－1 个1，同理可得，M 为Cordial 图，从而G 为Cordial 图.

图1 定理1 中情况2 的3－正则图标号

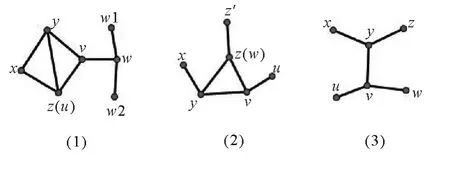
图2 解释引理4

引理3 对于有最大度ΔG=Δ 的图G，存在标号f，使得|v0(G)－v1(G)|≤1，|e0(G)－e1(G)|≤2Δ，且有如下结论:

(i)当e0(G)－e1(G)=2Δ 时，存在{x，y}⊂V(G)，使得{f(x)，f(y)}={0，1}，d(x)=d(y)=Δ，且顶点x，y 的标号分别与它们的邻点标号相同;

(ii)当e0(G)－e1(G)=－2Δ 时，存在{x，y}⊂V(G)，使得{f(x)，f(y)}= {0，1}，d(x)=d(y)=Δ，且顶点x，y 的标号分别与它们的邻点标号不同.

证明: 设C ⊂V(G)，{x，y}⊂V(G)－C，且xy ∉E(G)，f 是C 的一个标号，当V(G)－C 没有标号时，约定Vi(G)=Vi(C)，ei(G)=ei(G［C］).设x 在C 中的邻点有q 个标0，r 个标1，y 在C 中的邻点有s 个标0，t 个标1.那么，当令f(x)=0，f(y)=1 时，e0－e1的增量是q+t－r－s;当令f(x)=1，f(y)=0 时，e0－e1的增量是r+s－(q+t)，这两个增加量总有一个非负，也总有一个非正.现规定，当e0(G［C］)－e1(G［C］)≤0 时，给{x，y}标号使得e0－e1的增量非负;当e0(G［C］)－e1(G［C］)＞0 时，给{x，y}标号使得e0－e1的增量非正.由于q+t ≤d(x)+d(y)≤2Δ，同理r+s ≤2Δ，因此若原来的－2Δ ＜e0(G［C］)－e1(G［C］)≤2Δ，总是可以定义{x，y}的标号，使得{f(x)，f(y)}={0，1}，－2Δ ＜e0(G［C ∪{x，y}］)－e1(G［C ∪{x，y}］)≤2Δ.进一步看出，若原来e0(G［C］)－e1(G［C］)＜2Δ，而e0(G［C ∪{x，y}］)－e1(G［C∪{x，y}］)=2Δ，必然是e0－e1的增量为正，即原来e0(G［C］)－e1(G［C］)≤0，如此，增加量e0－e1≥2Δ.因最大度为Δ，故此时必然是原来的e0(G［C］)－e1(G［C］)=0，且d(x)=d(y)=Δ，且顶点x，y 的标号分别与它们的邻点标号相同.结论(i)得证，同理可得结论(ii).

下面，在V(G)中挑选出不相邻的点对xi，yi，直到选不出这样的点对为止.剩下的没有不相邻的点必构成完全图Km，因为Δ(G)=Δ，所以m ≤Δ+1.给Km的顶点标号，使得|v0(Km)－v1(Km)|≤1，此时2Δ.设取出的不相邻点对为x1，y1;…;xk，yk，依照开始的规则和分析，逐次给以上点对标号，即可得引理3 的结论.

引理4 设G 为D(0，3)图，且G 中有一个分支Gk(|Gk|≥6)，则存在C={x，y，z，u，v，w}⊂V(Gk)，使得{xy，yz，yv，uv，vw}⊂E(G［C］)，其中u 和z 或者x 和w 可能重合.

证明:(i)若Gk中含K4－e，首先给K4－e 如图2(1)的标号(顶点u 与z 重合)，设w ∈N(v)－{u，y}，∵，∴，设N(w)={v，w1，w2}，则w1，w2至多有一个与x 重合，如图2(1);

(ii)若Gk中含C3但不含K4－e，设C3的三个顶点为y，z，v，v 在C3以外的各邻点为x，z′，u，因Gk中不包含K4－e，故x，z′，u 任意两点不重合，如图2(2);

(iii)若Gk中不含C3，任取其两相邻顶点记为y，v，设N(y)={x，z，v}，N(v)={y，u，w}，因Gk中不含C3，故x，u，z，w 任意两点不重合，如图2(3).

由(i)(ii)(iii)，命题得证.

定理2 所有的D(0，3)图均为Cordial 图.

证明:(i).若G 为D(0，3)图，则G=A ∪B，其中A 为3－正则图，B 为由孤立点构成的图.根据文献［9］，当时，A 为Cordial 图，由引理1，G 为Cordial 图.

(ii).当A 不是Cordial 图，即|A|=8n+4，则，且由［11］知，e0(A)为偶数，故e0(A)－e1(A)≡2(mod 4).若A 的每个分支的阶都不大于4，由定理1 可得结论;否则，若A 中含K4，则A=K4∪H，其中H 为8n 阶3－正则图，由［3 ～4］，H 为严格Cordial 图，且容易验证K4∪K1是Cordial 图，故A∪K1=K4∪H ∪K1为Cordial 图，由引理1，G=A ∪B 为Cordial 图.接下来讨论A 中不含K4的情况，此时G 的每个分支Gk的阶数至少为6.

根据引理3，在图A 上存在标号f，使得|v0(A)－v1(A)|≤1，|e0(A)－e1(A)|≤2Δ=6，因为|A|=8n+4，故此时必有v0(f;A)=v1(f:A).因e0(A)－e1(A)≡2(mod 4)，故此时e0(f:A)－e1(f:A)∈{±2，±6}.当e0(A)－e1(A)=－6=－2Δ 时，由引理3(ii)A 中必存在标号如图3(1)(2)的3 度点，把A ∪{p}中的孤立点p 标号为0，把图3(1)中的三度点x 改标号为1，则图A ∪{p}获得标号，使得

图3 e0(A)－e1(A)=±6 时，A 中存在的顶点标号

或者把图3(2)中的三度点y 改标号为0，把A∪{p}中的孤立点p 标号为1，则图A ∪{p}获得标号，使得

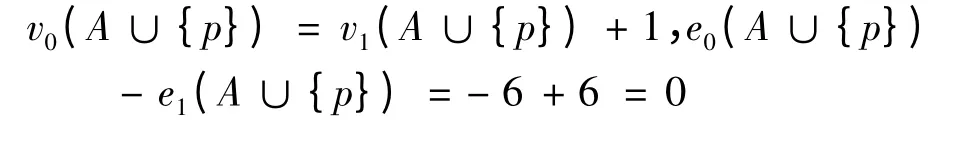
当e0(A)－e1(A)=6 时，由引理3(i)A 中必有标号如图3(3)(4)的3 度点，把A ∪{p}中的孤立点p 标号为0，把图3(3)中的三度点a 标号为1，则图A ∪{p}获得标号，使得

或者把图3(4)中的三度点b 标号为0，把A ∪{p}中的孤立点p 标号为1，则图A ∪{p}获得标号，使得

当e0(A)－e1(A)=±2 时，因|Gk|≥6，由引理4，A 中存在形如图2 的子图(其中u，z 或者x，w可能重合)，给C={x，y，z，u，v，w}标号为令f(y)=f(v)=0，然后在G［{x，z，u，w}］中选度最小的顶点x 标0，其他3 个顶点标1.

当e0(A)－e1(A)=－2 时，令f(v)=1，并把A ∪{p}中的孤立点p 标号为0，则

当e0(A)－e1(A)=2 时，令f(y)=1，并把A∪{p}中的孤立点p 标号为0，则.

综上所述，当e0(A)－e1(A)=±6 和±2 时，

即A ∪{p}是Cordial 图，由引理1，G=A ∪B=A ∪{p}或者G=A ∪B=A ∪{p}∪{其它孤立点}是Cordial 图.定理得证.

［1］ Ringel.G.，Problem 25，in:Theory of Graphs and Its Applications［C］.Proc Symposium Smo－ lenice Prague，1963:162－167.

［2］ Rosa.A.On Certain Valuations of the Vertices of a Graph［C］.Theory of Graphs，1966，(7):349－355.

［3］ G.S.Bloom and S.W.Golomb，Numbered Complete Graphs，Unusual Rulers，and Assorted Applications，Theory and Applications of Graphs［M］.Springer－Verlag，NewYork，1978，(642):53－65.

［4］ M.Sutton，Summable Graphs Labelings and their Applications.(Ph.D.Thesis)［D］.Dcpt.Computer Science，The University of Newcastle，2001.

［5］ Joseph A.Gallian，A Dynamic Survey of Graph Labeling，the Electronic Journal of Combinatorics［J］.2012，(19):51－58.

［6］ Cahit I.Cordial graph:A Weak Version of Graceful and Harmonious Graphs，Ars Combin［J］.1987，(23):201－207.

［7］ M.A.Seoud and A.E.I.Abdel Maqsoud，On Cordial and Balanced Labelings of Graphs［J］.Egyptian Math.Soc，1999，(7):27－135.

［8］ Ni Chenmin，Liu Zhishan，On the Cordiality of Graphs，Ars Combin［J］.2014，(113):451－455.

［9］ Liu Zhishan，Zhu Biwen，A Necessary and Sufficient Condition for A 3－Regular Graph to be Cordial.Ars Combin［J］.2007，(84):225－230.

［10］ 徐丽平，刘峙山，倪臣敏，2－正则图的Cordial 性，延边大学学报(自然科学版)［J］.2008，(03):21－22.

［11］ 刘峙山，堵根民，三正则连通图的Cordial 性，数学研究，2007，(03):114－116.

［12］ Bondy J.A.and Murty U.S.R.，Graph Theory with Applications［M］.New York:American Elsevier，1976.