水下液压冲击器活塞的设计分析①

陈 振，孙红旗，刘新柱，周 俊

(佳木斯大学机械学院，黑龙江 佳木斯154007)

0 引 言

水下液压冲击器是为清除水下管道钢筋混凝土而设计的机具.目前市场还没有相关产品，故必须根据现有的相关技术，并结合实际工作要求进行研制.在设计时要求通过理论分析来确定相关的设计参数，在初步设计完成以后，还需要根据理论分析来验证设计的合理性和正确性.本文将对此水下液压冲击器活塞的设计进行检验，对水下液压冲击器设计的理论分析方法进行初步探讨.

1 水下液压冲击器的工作原理

水下液压冲击器，通常是通过改变液压油的流动方向来改变活塞杆的受力情况，从而实现活塞杆高速往复运动.采用这种工作方式，可以使得液压冲击器的工作原理简单，并容易于实现.

如图1 工作原理简图所示，1－氮气室，2－变压腔，3－常高压腔.冲击器通过使变压腔液压油压力发生周期性的变化的方式，使冲击器活塞杆的受力情况发生周期性变化，从而使活塞杆发生循环往复运动，达到清除水下管道钢筋混凝土的目的［1］.

由液压冲击器工作原理可知，活塞杆在运动中能否形成对钢筋混凝土的冲击，取决于配油阀阀芯的运动状态.而阀芯的往复运动是由系统压力的变化来驱动实现的，水下液压冲击器系统压力通过控制阀芯的往复循环运动，从而实现对冲击活塞杆运动的控制，要使此工作原理得以顺利实现，冲击器系统压力在回程的时候需要缓慢提高.故需要通过分析冲击器活塞杆在运动过程中的受力情况来研究活塞的运动情形［2］.

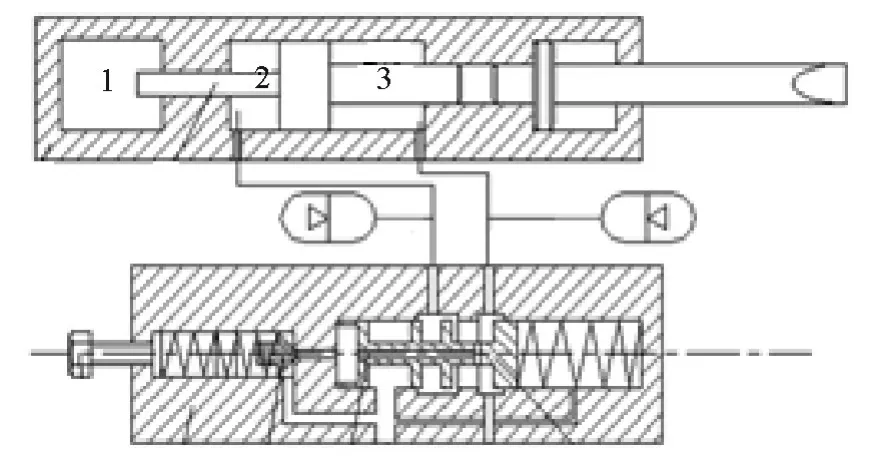
图1 液压冲击器的工作原理简图

2 活塞杆的动力学分析

2.1 活塞杆冲程时的动力学基本方程

由图2 可列出活塞杆冲程时的动力基本学方程为

这里，F01－变压腔对活塞的压力，F02－常高压腔对活塞的压力，F1－氮气室对活塞的压力，F2－液压油对活塞杆的阻力，F3－活塞杆运动时的摩擦阻力，m－活塞杆的质量，F4－活塞工作时受到的外载荷［3］.

这里密封空间中气体的压力设为p，密封空间中气体的体积设为V，氮气室的最小工作压力设为p1min，其初始最大容积设为V1max，活塞受到的压力作用面的面积设为A3，活塞杆运动时的动力学方程为

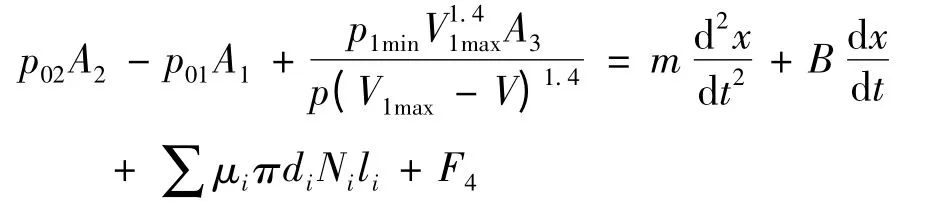
其中，p01为变压腔压强;p02为常高压腔压强;B 为粘性阻尼常数，A1为变压腔对活塞的压力面积，A2为常高压腔对活塞的压力面积;μi为密封圈与活塞杆的摩擦常数，di为活塞杆与密封圈接触处的直径，Ni为活塞杆密封侧面的压力，li活塞杆密封侧面长度.

对上述方程进行求解，可以得到活塞杆在冲程运动时，行程s 和时间t 的关系表达式.这里为了便于计算需要对高阶微分方程进行降阶处理.

图2 冲程时活塞杆的受力图

2.2 活塞杆回程时的动力学基本方程

在活塞杆的回程过程中，变压腔压力值等于零.此时氮气室被活塞压缩，氮气的压力阻碍了活塞的运动，由此得回程时的动力学基本方程为

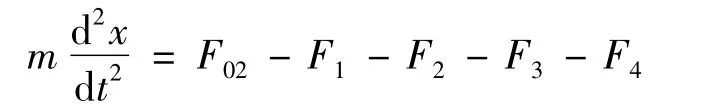
根据上式得微分方程

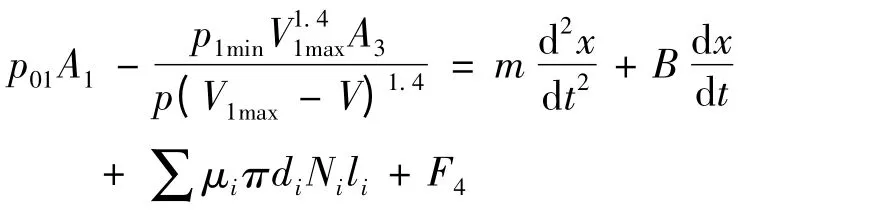
2.3 活塞杆冲程、回程动力学方程运动的分析

对于活塞杆在两个行程中的动力学微分方程，我们这里利用“Runge－Kutta”方法，对其动力学微分方程求解.

取开始步长0.0008，在这里取时间为横坐标轴，活塞杆的行程为纵坐标轴.得活塞杆在回程时的时间与行程的对应关系曲线(图3).由图可知，在运动的开始阶段，活塞杆行程随时间变化平稳，在运动的中期阶段，活塞杆行程随时间逐渐加快.同时随着行程的递增，变压腔的压力也在逐渐递增，当变压腔的压力增加到一定的数值时，对运动的影响较大，行程随时间变化减慢.当活塞杆运动到行程末端时，活塞杆受力情况发生改变，此时其的速度也逐渐减小为零，行程曲线也逐渐趋于平缓.

图3 回程时活塞杆运动的时间与行程的关系曲线

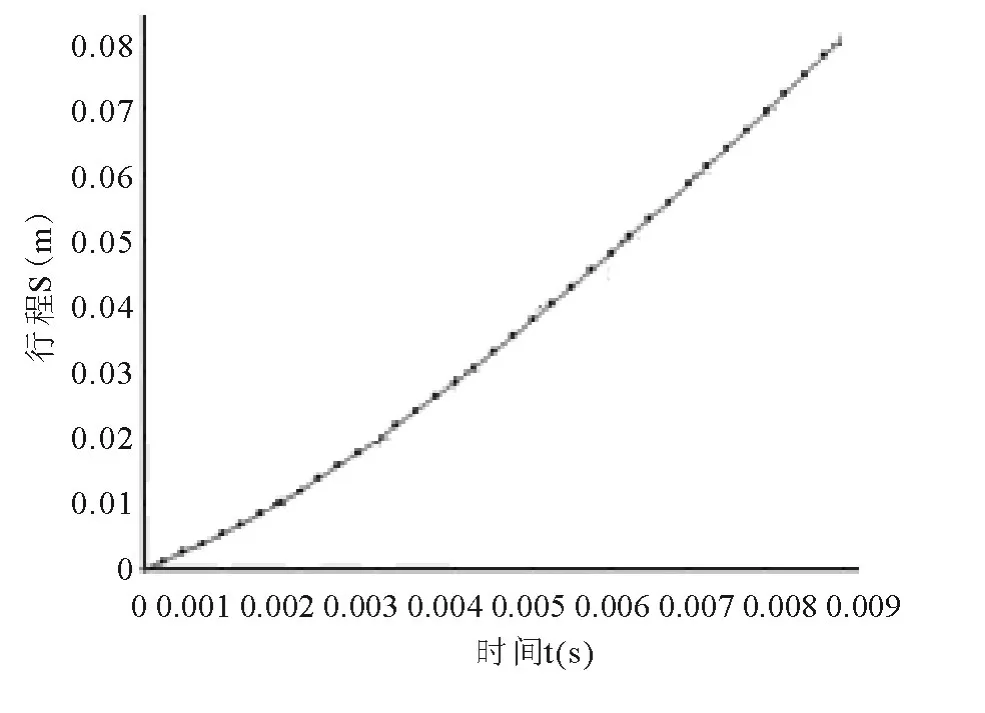
图4 冲程时活塞杆的行程与时间的关系曲线

这里采用同样的方法亦可绘制出活塞杆在冲程阶段的时间与行程的对应关系曲线(图4).因为设计时没有考虑冲击器活塞杆与铲头发生碰撞的具体情况，所以，在对水下液压冲击器的整体结构进行设计时，在活塞杆的冲程结束位置应该有起缓冲作用的结构.

活塞杆运动的最大行程设为80mm，上面的分析计算也是以此为前提的.因此计算得出的运动频率为活塞杆的最小运动频率.根据活塞杆在两个行程中的时间与行程的对应关系曲线可知，当活塞杆在冲程s=80mm 时，时间t ≈0.009s;当活塞杆在回程s=80mm 时，时间t ≈0.025s，则液压冲击器的最小冲击频率为

2.4 活塞杆在冲、回程时的拟合曲线方程

由于活塞杆无论是在冲程阶段还是在回程阶段，他们的动力学方程都是微分方程，是关于时间与行程的离散数值，故在计算时，需要把这些离散数值转变为连续值.利用线性回归法，设得到的曲线坐标为(xi，yi)(i=1，2，…，n)，其中，n－位移与时间曲线上点的个数.当输入xi时，输出为yi，这里设模型的预测值为则总平方误差为:

这里E 是关于a0，a1，…，ak的函数，故可以求出E 对aj的一阶导数，

令上式为零，解出a0，a1，…，ak.

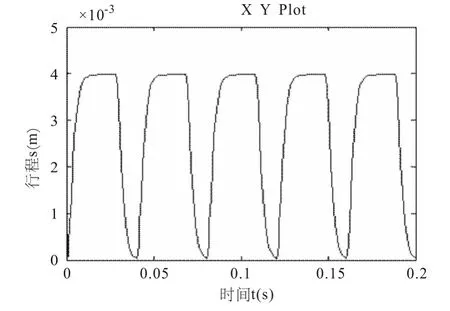
图5 阀芯的位移响应曲线

假设这些样本都通过此曲线，则有:

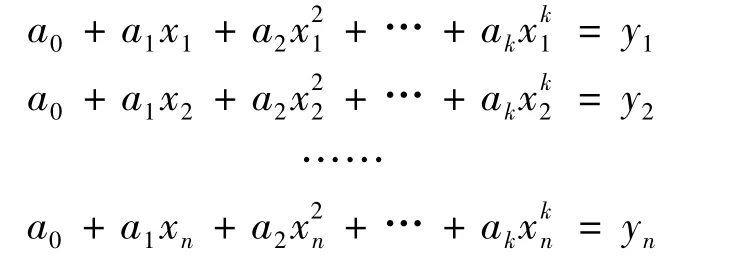
存在.于是有

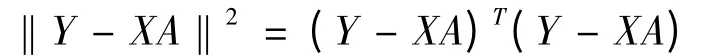
由分析可知，规定所得曲线与实际值的方差

利用上述曲线拟合的方法，求解活塞杆冲程时、回程时的时间与行程的表达式［4］.

表1 回程时的时间与行程的拟合数值

由此得活塞杆回程时的时间与行程的关系曲线表达式为

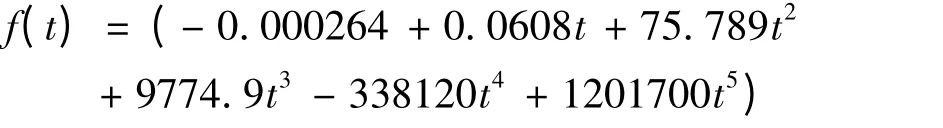
利用同样的方法，四阶拟合曲线所对应的曲线与求解微分方程得出的关系曲线形状相似，方差亦满足要求.由此得活塞杆冲程时的时间与行程的关系曲线表达式为

3 仿真分析

冲击器的压力随着活塞杆的运动而发生周期性变化，其频率在以上，当配油阀阀芯与锥阀芯都能够及时地响应此变化时，活塞杆快速往复运动的功能才能实现.故根据上述活塞杆的动力学方程及其拟合曲线方程，利用Matlab，同时结合配油阀阀芯的运动进行仿真分析.

当冲击器在工作过程中，调定压力为，控制锥阀芯运动的弹簧刚度系数为时，锥阀芯的位移响应曲线如图5 所示.由曲线可以知，阀芯对输入响应较好.冲击器系统在时间上非常精确地响应输入信号，从而保证了冲击器正常的工作［5］.

4 结 论

任何设计都必须以一定的理论分析为基础，而理论分析的结果反过来又能验证设计的合理性.本文对冲击器活塞杆的设计进行了相应的理论分析及校验.首先利用活塞杆的动力学方程，结合相应的数学分析方法，得出活塞杆在冲程和回程时的行程表达式.再利用“龙格－库塔”法对活塞杆两个行程的动力学微分方程进行求解，采用线性回归的处理方法来拟合曲线，从而得到活塞杆两个行程的位移与时间的解析表达式.最后结合配油阀阀芯的具体运动进行计算机仿真研究，验证了结论的合理性和正确性.

［1］ 刘贺平，孟庆鑫，房晓明.水下液压冲击器的机理研究［J］.哈尔滨工程大学学报，2005，26(1):88 －91.

［2］ 孟庆鑫，刘贺平，张岚弓，等.基于高速开关阀控制的液压冲击铲研究［J］.机床与液压，2004，(10):152 －154.

［3］ 刘贺平，罗阿妮.水下液压冲击铲关键技术分析［J］.哈尔滨工程大学学报，2006，27(6):878 －881.

［4］ 孟庆鑫，刘贺平，王立权，等.自反馈式水下液压冲击器冲击频率的确定［J］.哈尔滨工程大学学报，2005，26(2):179 －183.

［5］ LIU He－ping，LUO A－ni.Virtual Prototype Simulation on Underwater Hydraulic Impingement Shovel［J］.Journal of Marine Science and Application，2007，(1).