基于应变准则对管道横向滑坡响应规律的研究①

王黎明，署恒木，黄小光

(中国石油大学(华东)储运与建筑工程学院，山东 青岛266580)

0 引 言

滑坡是指山体斜坡上的岩土，在重力作用下沿着一定的软弱结构面(带)产生剪切位移而向斜坡下方移动的现象［1］.地震、强降雨等因素均可诱发山体滑坡.土体的永久性变形导致埋地管道产生不均匀沉降，从而引发管道弯曲、拉裂甚至整体失稳.对滑坡作用下埋地管道的应力、应变响应规律进行分析，可以判断埋地管道在滑坡等地质灾害作用下的失效行为，确定埋地管道的极限承载能力，为滑坡地质灾害下埋地管道的设计提供分析依据.

滑坡作用下埋地管道的分析模型涉及管道－土体的相互作用.近年来，国内外学者对于埋地管道的管土相互作用问题的进行了不同程度的研究［1～14］.张东臣根据不同的地滑力，分析了不同滑坡方向条件下管道的应力、应变分布［6］.刘慧基于管土相互作用的双线性模型，给出了管道在轴向滑坡、横向滑坡和深层圆弧滑坡作用下轴向应变的解析预测方法［7］.周晓莹等、王联伟等、练章富等分别利用有限元软件，考虑管土之间相互作用的非线性特征，模拟滑坡条件下管道的变形和应力特点，从不同角度研究了管道内压、滑坡长度、滑坡位移、滑坡方向与管道轴向的夹角等工程参数对管道应力的影响［8～10］.

本文根据薄壳大变形理论，利用ANSYS 软件建立横向滑坡作用下埋地管道的管土耦合模型，基于应变准则对埋地管道的有限元分析结果进行安全评价，并进一步探讨各种因素对滑坡条件下管道响应规律的影响.

1 横向滑坡管道的有限元模型

1.1 管材性能参数

以西气东输二线工程某管道为例，管材为X80HD2，管材力学参数如表1 所示，真实应力－应变曲线如图1 所示［11］.有限元分析中管材的本构模型采用Ramberg－Osgood 方程拟合.

表1 管道材料的力学性能

1.2 土弹簧模型及参数

滑坡作用下埋地管道的运动受到轴向、垂向及横向土体的作用，在有限元计算模型中，建立轴向、水平横向和垂直横向3 个方向的非线性土弹簧来模拟管土之间的耦合作用.取水平横向土弹簧为例，极限抗力－位移关系如图2 所示，Pu为极限抗力，xu为极限位移.土壤类型为砂土，土壤容重选取为18kN/m3，内摩擦角为35°，管道埋深为2.1m和1.8m 时的各个方向的弹簧参数，如表2 所示［11］.

图1 管道X80 应力－应变曲线

表2 土弹簧参数

1.3 位移载荷

滑坡过程中，埋地管道和周围土体都会产生不均匀的偏移，土体对管道的作用力难以精确描述.因此滑坡对埋地管道的作用通过施加位移载荷更为合理，而移位载荷形式以多项式最为简单［12～13］.如将坐标原点取在滑坡中心，如图3 所示，则位移载荷函数为偶函数.考虑到滑坡宽度两端位置管道变形的光滑连续条件，将滑坡位移载荷函数简化为四次多项式形式:

根据滑坡宽度及最大滑坡位移，结合滑坡宽度两端的光滑连续条件计算系数A，B.

图3 滑坡示意图

2 横向滑坡下管道的大变形分析

算例管道长度为60m，山体坡度为30°，管材为X80 钢管，内压为12MPa，管径为1.016m，壁厚为0.022m，埋深为2.1m，滑坡跨度为20m，滑移最大距离为1m.利用ANSYS 有限元软件建立滑坡条件下的管土耦合有限元模型，如图4 所示.管道采用shell181 单元，非线性土弹簧采用combin39 单元.考虑到滑坡坡角，在滑坡区域土弹簧上施加滑坡方向位移荷载，以模拟土体下滑对管道的作用.

图4 横向滑坡管道受力示意图

图5 管道位移

图5 为滑坡管道的位移矢量分布，最大值为0.853m，小于滑移的最大距离.管道的最大的Mises 应力为612MPa，在滑坡区域的正中心，即最大滑坡位移处.可知，管道已进入塑性阶段.最大轴向拉应变为0.0272，滑坡区正中心处取到，最大轴向压应变0.0197，在滑坡区与非滑坡区交界处取到.根据文献［14］中的应变设计准则，X80HD2 在断层中有内压的容许拉伸应变为0.0115，容许的压缩应变为0.76%，由此可以判断，埋地管道在滑坡条件下将发生失效.

图6 不同滑坡宽度下最大等效应力分布

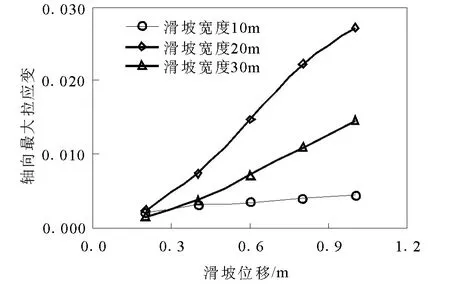
图7 不同滑坡宽度下最大轴向拉应变分布

3 管道滑坡响应规律分析

根据以上模型，分析滑坡位移、滑坡宽度、滑坡角度、管道埋深、管道内压等对管道响应规律的影响，计算参数如表3 所示.

表3 滑坡管道计算参数

图8 不同坡角下最大等效应力分布

图9 不同坡角下最大轴向拉应变分布

3.1 滑坡宽度的影响

以60m 为计算管道长度，取滑坡宽度10 ～30m 进行计算，分析滑坡宽度的影响.从图6 中发现在滑坡位移小于0.4m 的时，应力变化比较明显;大于0.6m 时，管道进入塑性阶段，应力变化比较缓慢.从图7 中发现滑坡宽度为20m 时，轴向拉应变最大，且随滑坡位移变化明显;而滑坡宽度为10m 时基本不随滑坡位移变化，此时土弹簧已进入塑性阶段，滑坡位移对管道变形影响不大.从20m和30m 的滑坡宽度比较下，相同的滑坡位移，滑坡宽度越小，管道所要承受的轴向拉应变越大，管道越易失效.因此，防止埋地管道局部的大位移滑动，能有效避免管道破坏.

3.2 滑坡坡角的影响

从图8 中发现在滑坡位移小于0.4m 的时，应力变化比较明显;大于0.4m 时，坡角为30°和45°的管道进入塑性阶段，而90°的管道还处于弹性阶段，但由于土弹簧失效，故三者应力变化都比较缓慢.从图9 中发现滑坡角度为90°时，轴向拉应变最小，且随滑坡位移基本不变，此时土弹簧已进入塑性阶段;而从30°和45°的滑坡角度比较来看，相同的滑坡位移，滑坡角度越小，管道轴向拉应变越大.

3.3 内压的影响

从图10 中发现在滑坡位移小于0.4m 的时，应力变化比较明显;大于0.6m 时，管道进入塑性阶段，应力变化缓慢.从图11 中发现滑坡位移小于0.4m 时，管道轴向拉应变基本不受内压影响，三种情况变化一致.滑坡位移大于0.4m 时，相同的滑坡位移，内压越大，管道轴向拉应变越大.

图10 不同内压下最大等效应力分布

图11 不同内压下最大轴向拉应变分布

图12 不同埋深下最大等效应力分布

3.4 埋深的影响

从图12 中发现在滑坡位移小于0.4m 的时，应力变化比较明显;大于0.4m 时，管道进入塑性阶段，应力变化缓慢.从图13 中发现相同的滑坡位移，埋深越大，管道承受的轴向拉应变越大，管道越易失效.这是由于管道的埋深影响土体对管道的约束程度，埋置越深，管道周围土体压实程度越高，管道所受的各向土反力越大，管道变形也就越大.因此，管道应尽量浅埋.

图13 不同埋深下最大轴向拉应变分布

4 结 论

结合有限元软件对横向滑坡管道进行了响应规律分析，得到如下结论:

(1)横向滑坡时，管道受到滑坡土体的作用，发生显著的弯曲变形，管道的高应力、应变主要出现在滑坡区中间和滑坡区与非滑坡区交界处3 个明显的弯曲区域，管道主要由于过大的轴向拉应变导致失效，必要时可使用柔性接头，提高管道的变形能力.

(2)滑坡宽度越小，管道所的轴向拉应变越大，滑坡角度越小，管道的轴向拉应变越大.因此，在沿坡铺设管道时，应注意山坡宽度与坡角，以防止埋地管道局部的大位移滑动.

(3)管道应尽量浅埋，管道内压不宜过大.

［1］ 周吉祥，何仁洋，高建，等.横向滑坡作用下埋地管道影响因素分析［C］.压力管道技术研究进展精选集－全国管道技术学术会议，2010.

［2］ 刘全林，杨敏.地埋管与土相互作用分析模型及其参数确定［J］.岩土力学，2004，25(5):728－731.

［3］ 李华，徐震，杨永和，等.滑坡作用下的埋地管道强度失效分析［J］.化工设备与管道，2012，49(6):54－57.

［4］ 朱秀星，仝兴华，薛世峰.跨越断层的埋地管道抗震设计［J］.油气储运，2009，28(10):30－33.

［5］ 闫相祯，张立松，杨秀娟.管道穿越地震断层管土耦合大变形壳模型的应变响应规律研究［J］.土木工程学报，2010，43(8):132－139.

［6］ 张东臣.滑坡条件下埋地管道受力分析［J］.石油规划设计，2001，2(6):l－6.

［7］ 刘慧.滑坡作用下埋地管线反应分析［D］.大连:大连理工大学，2008.

［8］ 周晓莹，郭永华，吕晓华，等.地质滑坡条件下不同因素对油气管道危险性影响分析［J］.工业安全与环保，2012，38(5):42－44.

［9］ 王联伟，张雷，董绍华，等.基于土弹簧模型的管道滑坡力学影响因素分析［J］.油气储运，2014，33(4):380－384.

［10］ 练章富，李风雷.滑坡带埋地管道力学强度分析［J］.西南石油大学学报(自然科学版)，2014，36(2):165－170.

［11］ 中国石油天然气股份有限公司管道建设项目经理部.Q/SY GJX 0135—2008 西气东输二线管道工程强震区和活动断层区段埋地管道基于应变设计导则［S］.北京:石油工业出版社，2008.

［12］ 张伯君.山体滑坡区域内长输埋地油气管道强度研究［D］.杭州:浙江大学，2013.

［13］ ZHENG JY，ZHANG BJ，LIU PF.Failure Analysis and Safety Evaluation of Buried Pipeline due to Deflection of Landslide Process［J］.Engineering Failure Analysis.2012，25:156－168.

［14］ 王国丽，韩景宽，赵忠德，等.基于应变设计方法在管道工程建设中的应用研究［J］.石油规划设计，2011，22(5):1－6.