一道“伪坐标系”考题引发的思考

☉江苏省如皋市实验初中 陈海宏

一道“伪坐标系”考题引发的思考

☉江苏省如皋市实验初中 陈海宏

近读《中学数学》，发现一个可喜的现象，即对中考命题或平时的期中、期末地区试题进行较有深度的探讨、商榷甚至批判（见文1～文5）.特别是文5，作者拿本地区的“权威考卷”说事，这种敢于批评与自我批评的态度值得点赞！特别是在当前不少命题研究的同行习惯于对中考题“唱赞歌”式的赏析相比，《中学数学》能集中刊发这么多命题商榷与批判的文章，也显示了编辑部这种倡导争鸣、说真话的胆略与勇气！受他们的启发和鼓励，作为一种实践响应，本文也拟就新近关注到一些考题展开命题探讨，就教于大家.

一、一道考题及思路突破

例1（某QQ群里同行的征解题）如图1，点A是反比例函数y=图像上一点，点B是x轴正半轴上一点，点C的坐标为（0，2），当△ABC是等边三角形时，点A的坐标为________.

解法一：如图2，在x轴的负半轴上取点D，使∠DCO=30°，在OB延长线上取点E，使BE=CD，连接AE，则∠BDC=60°，所以∠BCD+∠CBD= 120°.

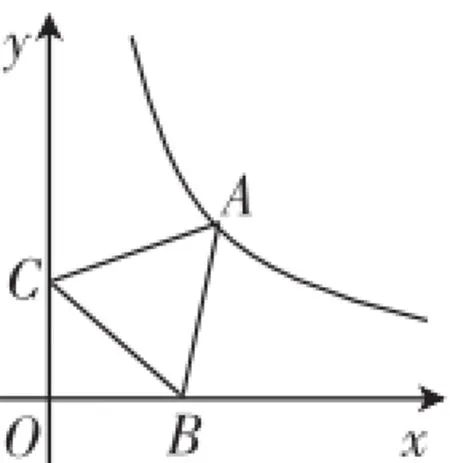
图1

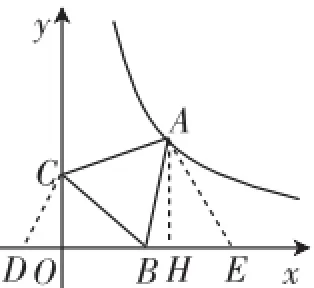
图2

因为△ABC是等边三角形，所以AB=BC，∠ABC= 60°，所以∠ABE+∠CBD=120°，所以∠ABE=∠BCD，所以△ABE≌△BCD，所以AE=BD，∠AEB=∠BDC=60°，所以BD，所以OD+HE=

解后反思：在上面的求解过程中，有两处是关键步骤：

第一，基于所谓“一线三等角”基本图形获得的启示，构造辅助线成为思路获得进展的关键.不妨链接一些常见的“一线三等角”图形：在图3中，点D、A、E在同一条直线上，∠BDA=∠BAC=∠AEC=90°，则有△BDA∽△AEC；在图4中，∠BDA=∠BAC=∠AEC，仍有△BDA∽△AEC.（注：如果恰有BA=CA，则△BDA≌△AEC）

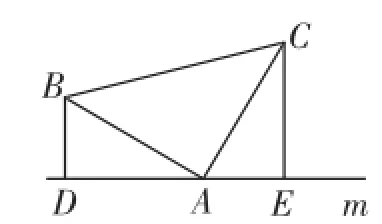
图3

图4

解法二：如图5，以OC为边，在第一象限作等边△OCD，连接AD，可证△ACD≌△BCO，∠ADC=∠BOC=90°.基于“一线三等角”基本图形的启示，过点D作DG∥x轴，交y轴于点G，过点A作AH⊥DG，垂足为H.可得

图5