一题多变培养学生的创造思维能力

☉浙江省宁波逸夫中学 华君飞

一题多变培养学生的创造思维能力

☉浙江省宁波逸夫中学 华君飞

在数学教学中，应对例题、习题的形式或题型作不断变化，克服教学中的思维定势，促使学生从多角度、多方位考虑问题，培养创造思维能力.下面结合一些例题，谈谈这个问题.

例1如图1，已知△ABC，以AB、AC为边向外作等边△ABD和等边△ACE，连接BE、CD，求证：BE=CD.

证明：由△ABD为等边三角形，得AD=AB，∠DAB=60°.

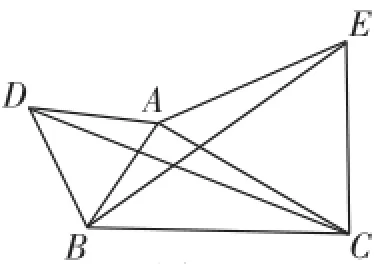
图1

由△ACE为等边三角形，得AE=AC，∠EAC=60°.

则∠DAB+∠BAC=∠EAC+∠CAB.

即∠DAC=∠EAB.

则△DAC≌△BAE.

则BE=CD.

变式1：如图2，已知△ABC，以AB、AC为边向外作正方形ABFD和正方形ACGE，连接BE、CD，则BE与CD有什么数量关系？请证明.

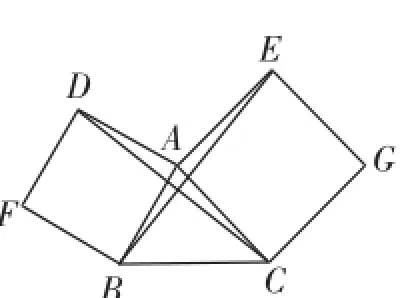
图2

分析：此题形变质不变，仍然可以通过证明△DAC和△BAE全等，得出BE=CD.

变式2：如图3，要测量池塘两岸相对的两点B、E的距离，已经测得∠ABC=45°，∠CAE=90°，AB=BC= 100，AC=AE，求BE的长.

分析：从例1和变式1两题的经验可构造一个三角形与△BAE全等，观察图形，可以△ABC的AB边为一直角边向外作等腰直角△ABD，连接CD、BE，可证得BE=CD.

图3

例2已知△ABC，如图4，点P是∠ABC和∠ACB的角平分线的交点，求证：

图4

变式1：如图5，若点P是∠ABC和外角∠ACE的角平分线的交点，试猜想∠P与∠A的关系，并说明理由.

图5

∠ACE=∠A+∠ABC.

由BP平分∠ABC，得∠ABC=2∠PBC.

由CP平分∠ACE，得∠ACE=2∠PCE.

则2∠PCE=∠A+2∠PBC.

变式2：如图6，若点P是外角∠CBF和∠BCE的角平分线的交点，确定∠P与∠A的关系，并说明理由.

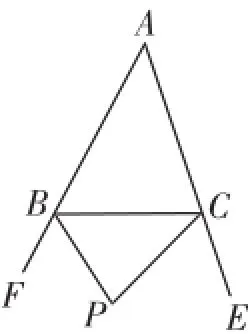
图6

由∠FBC=∠A+∠ACB，∠BCE=∠A+∠ABC，得∠FBC+∠BCE=∠A+∠ACB+∠ABC+∠A=180°+∠A.

从这个变式可以看出虽然条件与结论略有改变但基本是形变神不变，运用的知识点基本都是角平分线的性质及三角形外角的一个性质，通过变式练习巩固了基础知识，收到了举一反三的效果，训练了思维的灵活性，提高了能力，尤其是创造性思维能力.

总之，通过变式教育，能使学生进一步掌握数学知识间的内在联系，透彻理解教材，巩固所学知识，起到举一反三，触类旁通的作用，达到拓宽思维，发展智力，培养能力的目的.对于防止题海战术，减轻学生负担，提高教学质量，改变高分低能，提高学生的创造思维能力，有积极作用.Z