回转式贴标机夹标工位取标板运动分析与优化

李全来

（北京工商大学材料与机械工程学院，北京100048）

0 引言

贴标机是将标签贴于包装件指定位置上的一种常用包装机械，它能自动完成待贴标包装件的供送、包装件定位、标签供送、包装件贴标、标签抚平、已贴标包装件的输出等［1－3］。回转式贴标机指在贴标过程中包装件在贴标工作台上做回转运动的贴标机，具有结构紧凑、生产效率高、操作方便等优点。近年来，回转式贴标机广泛用于圆柱体包装件纸质标签的贴标。

回转式贴标机主要由取标机构、供瓶螺杆、星形拨轮、回转工作台、理标毛刷等组成［4］。工作时包装件通过供瓶螺杆和星形拨轮送入回转的贴标工作台，并转至贴标工位。与此同时，取标装置分别与胶辊和标盒、夹标转鼓接触，完成取标板上胶、取标，并用夹指将标签夹于夹标转鼓，随后送至贴标工位。当标签和待贴标包装件接触时标签粘到待贴标包装件指定位置上，经过理标毛刷抚平标签后通过出瓶螺杆输出，完成整个贴标工序。

取标装置是回转式贴标机的关键部件，决定了贴标机的工作效率和贴标质量［1－3］。它由取标板、胶辊、标盒、夹标转鼓、转盘、扇形齿轮、圆柱齿轮、槽凸轮、滚柱等组成。在凸轮—齿轮组合机构的控制下，取标板既随转盘公转又绕滚柱自转，完成上胶、取标和夹标动作。夹标工位取标板的运动规律直接决定了标签贴于待贴标包装件前的状态，对贴标质量有较大影响。为此，许多研究者针对夹标工位取标板运动规律的合理设计展开了研究。陈金元［5］提出夹标过程中取标板应保持匀速摆动，标签可以发生拱曲，在夹标工位终点取标板摆角为0°，并通过转盘转角计算了取标板摆角。肖仲湘［6］指出整个夹标过程中标签与取标板的最大剥离角不应超过75°，标签纸应保持拉直状态，建立了取标板摆角的计算方程。张俊玲［7］认为夹标工位标签与夹标转鼓斜交并计算了取标板摆角。张芙蓉［8］和兰云志［9］认为夹标工位取标板与夹标转鼓对滚，其运动过程与上胶工位相似，可用与上胶工位相同的方法计算取标板的摆角。

本文以夹标工位转盘转角增加量Δα和转盘与夹标转鼓的转速比I 为设计变量，以标签完全剥离点绝对误差函数为目标函数，以夹标过程中从取标板上剥离下来的标签始终保持拉直、标签最大剥离角度不超过75°，剥离下来的标签与夹标转鼓保持相切为约束条件，建立了夹标工位取标板运动优化模型，并用遗传算法求解，在实现夹标的同时减小标签的弯曲，提高贴标质量，为夹标工位取标板摆角的合理设计提供新方法。

1 夹标工位取标板运动分析

图1为夹标工位取标板摆角示意图。O0为转盘的回转中心，Ob为取标板的曲率中心，取标板的自转中心C 处于∠B1ObB2的角平分线上，偏心距为e，Rb为取标板半径，取标板弧长SB1B2与标签长度L 相等。取标板在自转的同时绕O0公转，公转半径为R0。O3为夹标转鼓的回转中心，R3为夹标转鼓半径。转盘和夹标转鼓均匀速转动，两者的转速比为I＝ω0/ω3。在夹标工位，夹标转鼓上的夹指夹住取标板上标签的一端B1。随着夹标转鼓的转动和取标板的摆动，标签被逐步从取标板上剥离下来。在此过程中，为防止涂有胶水的标签自粘，被夹指拉出的标签保持拉直，即夹指D 与取标板剥离点B 之间的标签段BD为一条直线段。同时，在任意时刻从取标板上剥离出来的标签长度BB1与BD 相等。α为转盘转角，β为取标板摆角，γ 为夹标转鼓转角，ε为标签的剥离角。剥离下的标签与夹标转鼓保持相切。

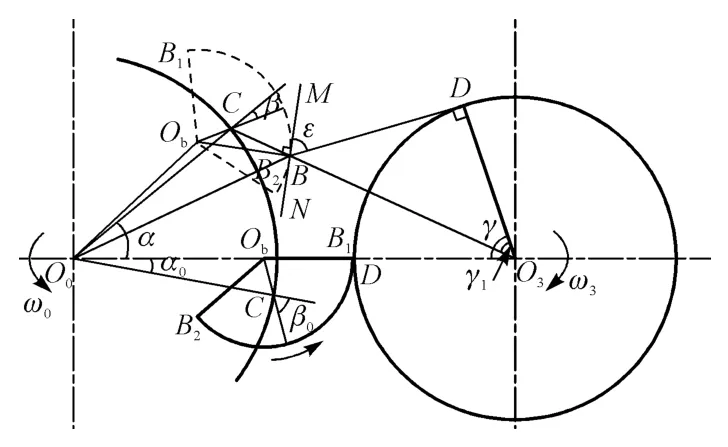
图1 夹标工位取标板运动分析

在夹标初始位置，取标板与夹标转鼓相切，O0、Ob、B1、D、O3共线，此时标签剥离点B 与取标板上标签的一端B1重合：

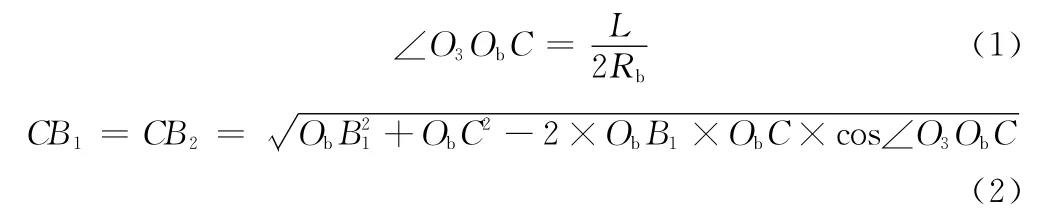
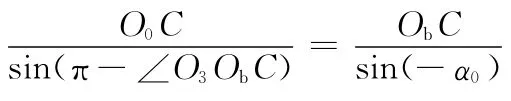
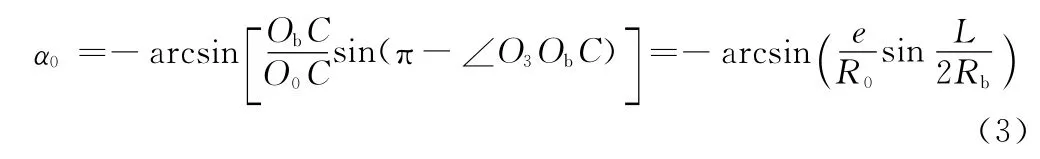
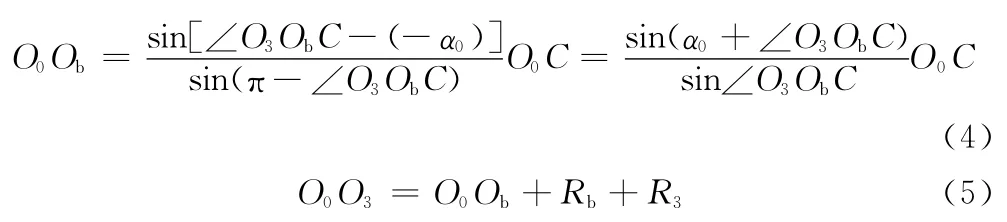
把式（4）代入式（5），可求得O0O3。

在初始位置，γ10＝∠BO3D＝0，β0＝∠O3ObC＋α0。当中心转盘转角为α，即∠CO0O3＝α时，由转速比可知：γ＝α/I。

当标签被均速剥离下来时，单位时间内BD 的变化量ΔBD相等，则：

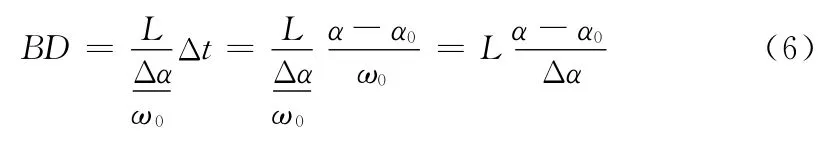
在△O3BD 中：

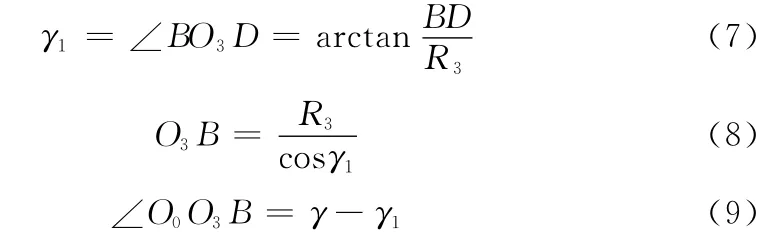
则：

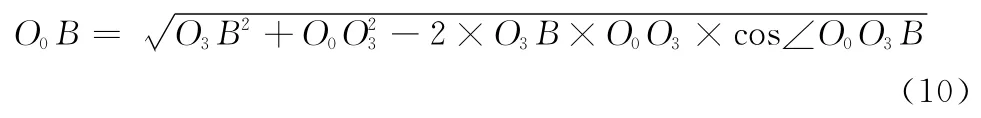
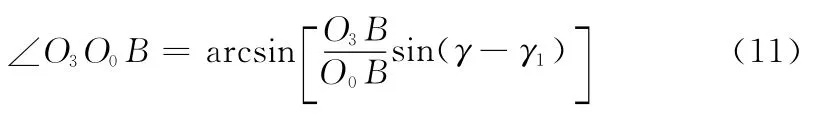
则：

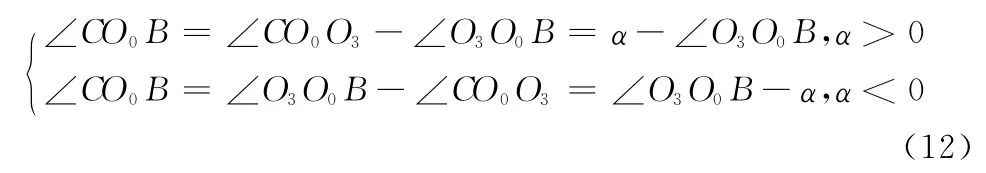
在△CO0B 中：

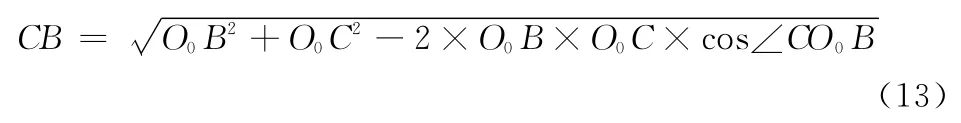
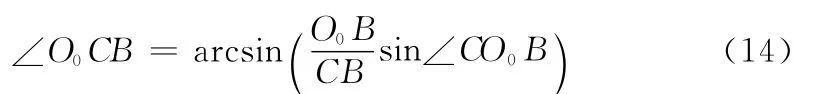
在△CObB 中：

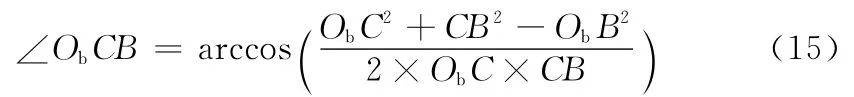
则标板摆角：

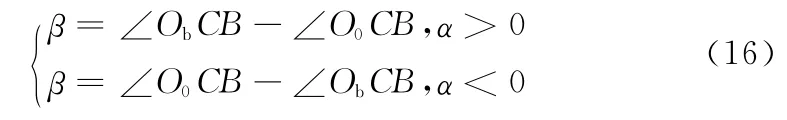
过B 点的取标板切线为MN：

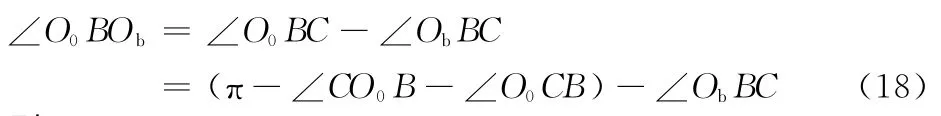
则：

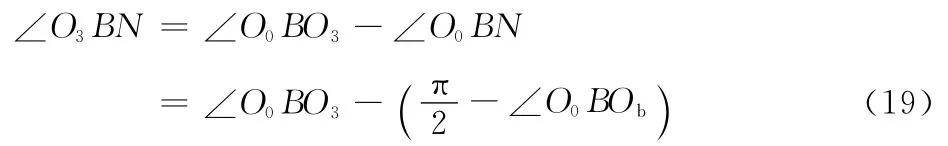
标签与取标板的剥离角为：

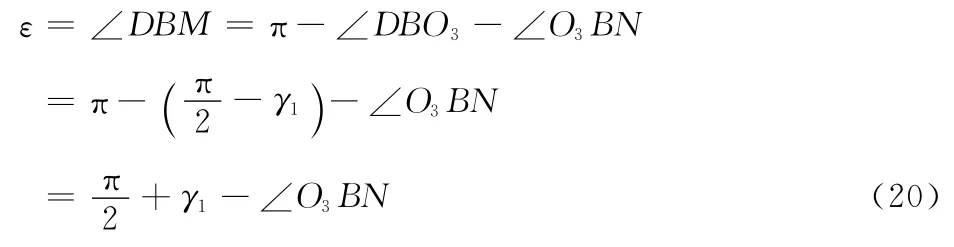
夹标工位终止位置处B与B2重合，此时转盘转角为αmax＝α0＋Δα，γ1max＝γ10＋Δγ1＝Δγ1。式中的Δα和Δγ1分别为转盘转角的增加量和γ1的增加量。当给定参数Δα和I 时，可以计算出取标板摆角β和标签剥离角ε。

2 夹标工位取标机构运动优化

2.1 优化模型的建立

当剥离下来的标签与夹标转鼓保持相切时，标签与取标板完全剥离处，可由式（11）得出CB（αmax，I）。此时标签剥离点B应与取标板上B2重合，则CB（αmax，I）＝CB2。因此，定义标签与取标板完全剥离处的剥离点绝对误差为ΔCB＝︱CBCB2︱。若ΔCB≠0，则说明标签与取标板完全剥离处标签剥离点B 与取标板上B2不重合，即取标板到达摆动终点位置标签尚未完全剥离，或者取标板尚未到达摆动终点位置标签已经完全剥离，这均会影响夹标质量。

以Δα和I 为设计变量，以ΔCB 为目标函数，以夹标工位标签从取标板上剥离出来后始终保持拉直，标签最大剥离角度不超过75°，剥离下来的标签与夹标转鼓保持相切为约束条件的夹标工位取标机构运动优化模型为：

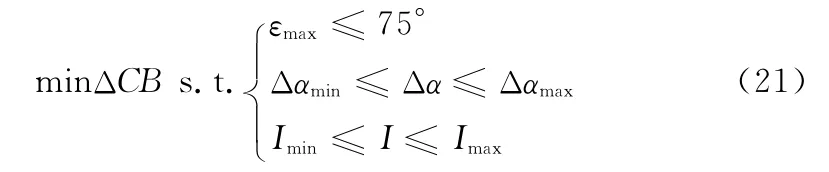
2.2 优化模型的求解

夹标工位取标机构运动优化问题的目标函数为非线性方程。传统优化方法在求解非线性优化问题时易陷入局部最优，而且计算时间较长。遗传算法将生物界中的选择和遗传机制引入搜索过程而形成的随机并行进化搜索算法，具有不易陷入局部最优的优势，适合求解非线性优化问题［10－11］。本文采用遗传算法求解夹标工位取标机构运动优化问题，基本步骤如图2所示。

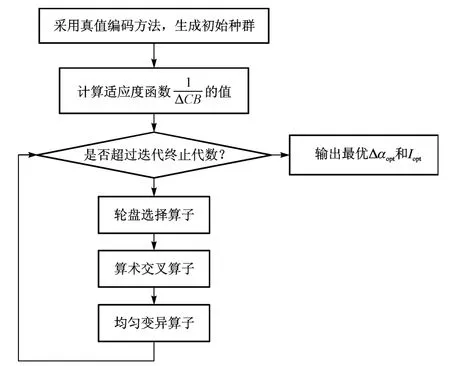
图2 夹标工位取标板运动优化流程

遗传算法操作时首先需要建立由若干个个体组成的初始种群。每个个体都是优化问题的候选解。采用真值编码方法［10－11］，每个基因位的值是设计变量的真值，个体可表达为X＝［Δα，I］。第i个个体Xi＝［Δαi，Ii］的每个基因值均通过随机法产生，即：

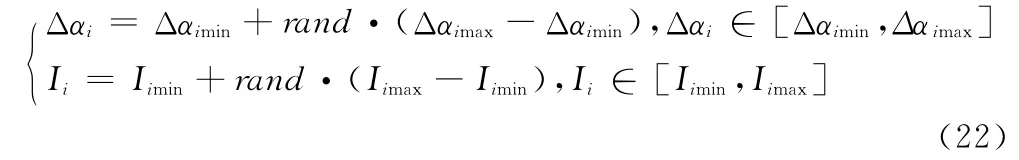
式中，rand 为生成的［0，1］之间的均匀随机数。

适应度函数是评价个体优劣的标准，是进行个体选择操作的主要依据［10－11］。本文以目标函数的倒数作为适应度函数Fit（x），即：

选择操作［10－11］是遗传算法的三个基本操作之一，适应度值越高的个体被选中进行遗传或者交叉操作的概率越大。本文选用比例选择算子［10－11］。

交叉操作［10－11］是遗传算法中产生新个体的主要方法，直接影响着遗传算法的全局搜索能力。本文通过算术交叉算子获得新个体。首先从种群中随机选出两个个体Xm＝［Δαm，Im］和Xn＝［Δαn，In］，随机选择要交叉的基因位进行线性交叉。如选择对基因位Δα进行交叉，则交叉运算后产生的两个新基因值Δαm′和Δαn′分别为：

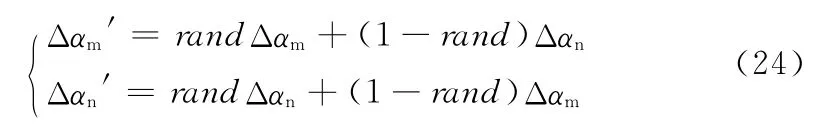
生成的新个体可表达为Xm′＝［Δαm′，Im］和Xn′＝［Δαn′，In］。

变异算子［10－11］指将个体的某些基因位上的基因值用其他基因值替换从而生成一个新个体的方法。它与交叉算子配合使用，能提高遗传算法的局部搜索能力。本文采用均匀变异算子。

3 优化结果与分析

本文选用的设计参数：标签长度L 为130mm，取标板半径Rb为54mm，取标板偏心距e为14 mm，夹标转鼓半径R3为130mm［5，12］。转盘转角增加量30°≤Δα≤60°，转盘与夹标转鼓的转速比0≤I≤1。初始种群规模选择M＝100；交叉概率pc＝0.75，变异概率pm＝0.15；迭代次数为25次。

遗传算法优化结果如图3 所示。优化后最优最大转盘转角Δαopt＝39.991 9mm，转盘与夹标转鼓的最优转速比为Iopt＝0.664。将Δαopt和Iopt代入夹标工位取标板运动分析方程式（15）和式（18）后，即可求出相应的取标板摆角和标签剥离角度，此处不再赘述。

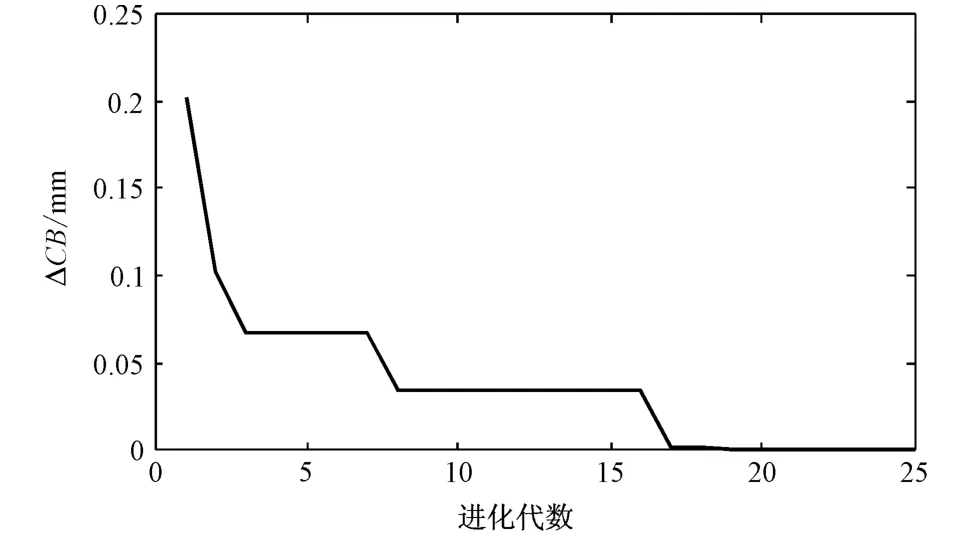
图3 夹标工位取标板运动的优化

4 结语

本文分析了回转式贴标机夹标工位取标板的运动规律，建立了取标板摆角和标签剥离角的计算方程。以转盘转角增加量和转盘与夹标转鼓的转速比为设计变量，以标签与取标板完全剥离处的剥离点绝对误差为目标函数，以从取标板剥离出的标签始终保持拉直，标签最大剥离角度不超过75°，标签与夹标转鼓保持相切为约束条件，建立了夹标工位取标板运动优化模型。用遗传算法求解该优化模型，结果表明，采用优化后转盘转角增加量和转盘与夹标转鼓的转速比能实现有效夹标，并减小夹标过程中标签的弯曲，提高贴标质量，从而为取标装置的合理设计提供了新方法。

［1］孙智慧，晏祖根.包装机械概论［M］.3版.北京：印刷工业出版社，2012：157－164.

［2］黄颖为.包装机械结构与设计［M］.北京：化学工业出版社，2007：153－161.

［3］伍志祥，陆佳平，林淼.贴标机自动取标贴标的研究与分析［J］.机械设计，2013，30（12）：62－64.

［4］金国斌，张华良.包装工艺技术与设备［M］.2版.北京：中国轻工业出版社，2009：167－175.

［5］陈金元.回转式贴标机贴标部件的运动分析及凸轮设计原理［J］.无锡轻工业学院学报，1992，11（1）：52－61.

［6］肖仲湘.贴标机凸轮齿轮组合机构的研究［J］.轻工机械，2000（1）：21－26.

［7］张俊玲.回转式贴标机凸轮的设计与研究［D］.济南：山东大学，2006：15－18.

［8］张芙蓉.贴标机取标机构设计探讨［J］.轻工机械，1998（2）：21－24.

［9］兰云志，李乐山.高速贴标机数学模型研究与参数设计［J］.轻工机械，2003（1）：33－36.

［10］余胜威.MATLAB 优化算法案例分析与应用［M］.北京：清华大学出版社，2014：227－249.

［11］雷英杰，张善文.MATLAB 遗传算法工具箱及应用［M］.2版.西安：西安电子科技大学出版社，2014：43－59.

［12］李全来.回转式贴标机上胶工位凸轮曲线优化［J］.轻工科技，2014（12）：48－50.