基于视频数据的交叉口状态判别及排队长度估计
2015-04-13唐少虎刘小明陈兆盟
唐少虎, 刘小明, 陈兆盟
(北方工业大学 城市道路交通智能控制技术北京市重点实验室, 北京 100144)
基于视频数据的交叉口状态判别及排队长度估计
唐少虎, 刘小明, 陈兆盟
(北方工业大学 城市道路交通智能控制技术北京市重点实验室, 北京 100144)
为了评价信号控制交叉口的交通状态及估计周期排队长度,本文以集散波为理论基础,分析视频检测的机动车通过上下游相邻交叉口的数据,提出了基于车辆延误时间的交叉口交通状态判别划分,进一步设计了欠饱和及饱和交通状态下的交叉口最大排队长度估计方法. 实例分析表明,本文方法所估计的排队长度比较接近实际调查值,排队相对误差在可接受的范围内,结果验证了所设计的排队长度估计方法是有效可行的.
视频数据; 集散波; 交通状态判别; 最大排队长度估计
0 引言
信号控制交叉口的交通状态判别对于交通管理有着重要的意义,其结果直接影响了路况信息发布和交通控制与诱导的有效性和准确性. 路网交通状态本质上是交通流的时空变化,交通流的不同时空分布代表不同的交通状态. 信号控制交叉口不同时段下的交通流分布同样反映交叉口的通行状态,通过研究及判别交叉口的交通状态,并在此基础上对进口车道机动车排队长度的实时变化情况进行估计,可为交通管控、交通运行评价和交通信息服务提供精确的实时交叉口状态分析,从而进一步为缓解交叉口交通拥堵、改善出行条件和提高通行效率提供有效的交通信息支撑.
传统的排队长度研究有排队论、集散波、概率论、神经网络或者历史交通流数据等方法,也有研究者利用新技术采集浮动车或图像数据等方法以改进算法结果的精度. 代磊磊[1]采用历史交通流量数据建立流量预测模型,并基于定数排队理论建立了排队长度计算模型,实现对饱和信号交叉口排队长度的预测,但是并没有给出欠饱和状态下的预测模型以及没有说明路口检测器的类型及数据处理过程. 王进[2]基于集散波理论建立了最大排队长度模型,提出了时空协调指数及其计算方法,研究表明该模型能定量计算不同时空参数下的最大排队长度值,但是并没有通过实际路口数据验证该模型. 王殿海[3]以集散波理论为依据,分析了不同周期和相位差条件下相邻交叉口的排队情况,同样该结果只是以模拟的方式进行了验证分析. 祁宏生[4]根据路段交通流流向关系建立了神经网络和贝叶斯网络2种模型,并用仿真路网对2个模型进行了有效性验证,但是没有从本质上给出排队长度变化的机理关系. 荣建[5]在SIGNAL94模型的基础上建立了动态计算的排队长度优化模型,并对数据进行了时间平滑处理,最后用实测数据进行了精度分析以验证模型的有效性,但是在拥挤状态下的精度有所下降. 何宁[6]通过大量的调查数据拟合出交叉口平均排队车数的计算方法,并对实际路口进行了相关指标预测,但是该值并不能精确反映交叉口的实际排队状况. Comert和Ban[7-8]分别采集浮动车数据对排队长度进行估算,或利用概率论导出排队长度模型或得到机动车延误时间进行排队分析. 庄立坚[9]利用浮动车GPS位置数据估算交叉口最大排队长度,设计了计算和修正方法,最后对实际交叉口进行了实例分析证明了方法的可行性,该方法精度依赖于浮动车比率大小且算法较为复杂.
交叉口车辆延误时间和排队长度在一定程度上反映出交叉口的交通状态,通过实时监测车辆延误和估计排队长度来评价交叉口通行状态已经成为交通状态判别的一个研究方向. 本文以视频实时监测数据为基础,处理并分析机动车通过上下游交叉口的交通流量和通过时间,通过集散波理论在得出交叉口车辆延误时间的基础上,提出了基于车辆延误时间的交叉口交通状态判别方法,并进一步设计了在欠饱和与饱和交通状态下的交叉口排队长度估计方法.
1 视频数据检测原理
视频监控、卡口以及电子警察系统已经被广泛应用于城市交通管理,其中的关键技术是视频图像检测技术. 通过对视频数据信息的处理和分析,可以得到道路上行驶的机动车牌照信息,并且可以通过当前系统时间获取机动车通过视频监控点的具体时间. 理论上,不考虑恶劣天气等客观因素,在交叉口4个方向车道上安装视频监控系统,现场安装位置如图1,通过交叉口的所有机动车都可以被检测到车牌信息以及通过交叉口的时间. 以上下游2个交叉口为例,一辆机动车通过上游和下游交叉口的时间都可以被精确记录下来,那么可以得到该机动车通过2个交叉口的行程时间. 整理后可得到如表1所示数据. 其中,行程时间可通过管理中心的系统后台服务器计算获得,全部数据可存储在数据库中供用户提取使用. 视频监控系统全局结构如图2所示.

图1 视频检测安装平面图

图2 视频检测系统全局结构图

LicenseplatenumberUpstreamdetectiontimeDownstreamdetectiontimeTraveltime京BL632X2014⁃02⁃03,11:35:432014⁃02⁃03,11:36:210:00:38
2 基本概念与分析
2.1 集散波原理
机动车通过信号控制交叉口最多会经过5种行车状态,即匀速、减速、停车、加速到匀速. 如果交叉口的交通信号是绿灯,机动车则不会有减速到停车再到加速的过程. 为了便于分析,集散波理论理想化了机动车行车状态,车辆排队集散波过程如图3所示. 如果前方交叉口的信号灯为红灯状态,机动车减速行驶到进口车道的排队车辆队尾并停车排队,后续的机动车都会依次停车排队,将此机动车排队的过程称之为排队集结波(Queuing Shockwave),图3中w1为集结波速. 交叉口绿灯放行后,排队的机动车从前向后依次启动并加速通过进口车道,将此过程称之为排队消散波(Discharging Shockwave),图3中w2为消散波速. 如果下游路段为非拥堵状态,也没有出现交通事件等异常现象,那么消散波速一般大于集结波速,当消散波与集结波相遇时,该进口道达到最大排队长度Lmax. 需要指出的是,实际进口车道的机动车到达率是随机无规律的,图中车辆到达呈均匀分布且交叉口无剩余排队车辆.

图3 信号控制交叉口车辆排队集散波示意图
集散波理论从Lighthill-Whitham-Richards(LWR)交通流模型[10-11]演化而来,其中,波速的计算公式为
(1)
式中,q1和q2为上游和下游的交通流量;k1和k2为上游和下游的交通流密度;u2和u1为上游和下游的交通流平均速度.
假设下游路段不拥堵,当交叉口绿灯放行后,排队的机动车以饱和流率通过交叉口,消散波即从停车线向上游扩散,依据式(1)可得到消散波的波速
(2)
式中,qm为饱和交通流率;km为饱和交通密度;kj为堵塞交通密度;um为饱和交通流速度.
2.2 交通状态判别
道路交通状态可分为3种情况:欠饱和、临界饱和以及饱和状态. 3种交通状态可分别定义如下:欠饱和指在有效绿灯时间内完全清空交叉口排队车辆,即绿灯放行的车辆没有达到交叉口能够通过的最大通行量;临界饱和指在有效绿灯时间内接近或者刚好清空排队的车辆,即放行车辆将要或者达到交叉口能够通过的最大通行量;饱和指在有效绿灯时间内无法清空排队等待的车辆,即排队等待的车辆已经超过交叉口所能放行的最大通行量. 需要指出的是,此处的饱和是指1次绿灯时间已经无法完全清空排队车辆,出现了车辆2次排队以等待下次绿灯放行.
交通信号控制系统SCATS提出了饱和度的概念,其定义是被车流有效利用的绿灯时间与绿灯显示时间之比. 可以理解为,当路段车流量较低时,车队离散程度较大,饱和度较低,交通处于畅通状态,即欠饱和状态;当路段流量较大或者交叉口进行绿波协调控制时,车队持续存在,饱和度较高,这时难以判断交叉口处于何种状态. 而依据机动车通过相邻交叉口的时间,根据集散波理论可以较好地解决这个难题.

图4 欠饱和交通状态延误示意图

图5 饱和交通状态延误示意图
在欠饱和交通状态下机动车延误如图4所示,在饱和交通状态下机动车的延误如图5所示. 以两个相邻路口为例,机动车i通过上下游交叉口的时间分别为t′i,ti,通过上游交叉口后机动车i以速度ui行驶至排队车辆队尾D点并停车等待,下游交叉口绿灯放行后,消散波传播至C点后,机动车i以饱和交通速度um通过交叉口. 从图4、5可得到,如果下游交叉口没有控制信号,理论上机动车i通过下游交叉口的时间应为tn,而实际通过时间为ti,从而可得到延误时间为Tdelay. 在欠饱和状态下,理论上机动车停车等待的延误时间一般不会超过下游交叉口的红灯时间,如图5所示Tdelay
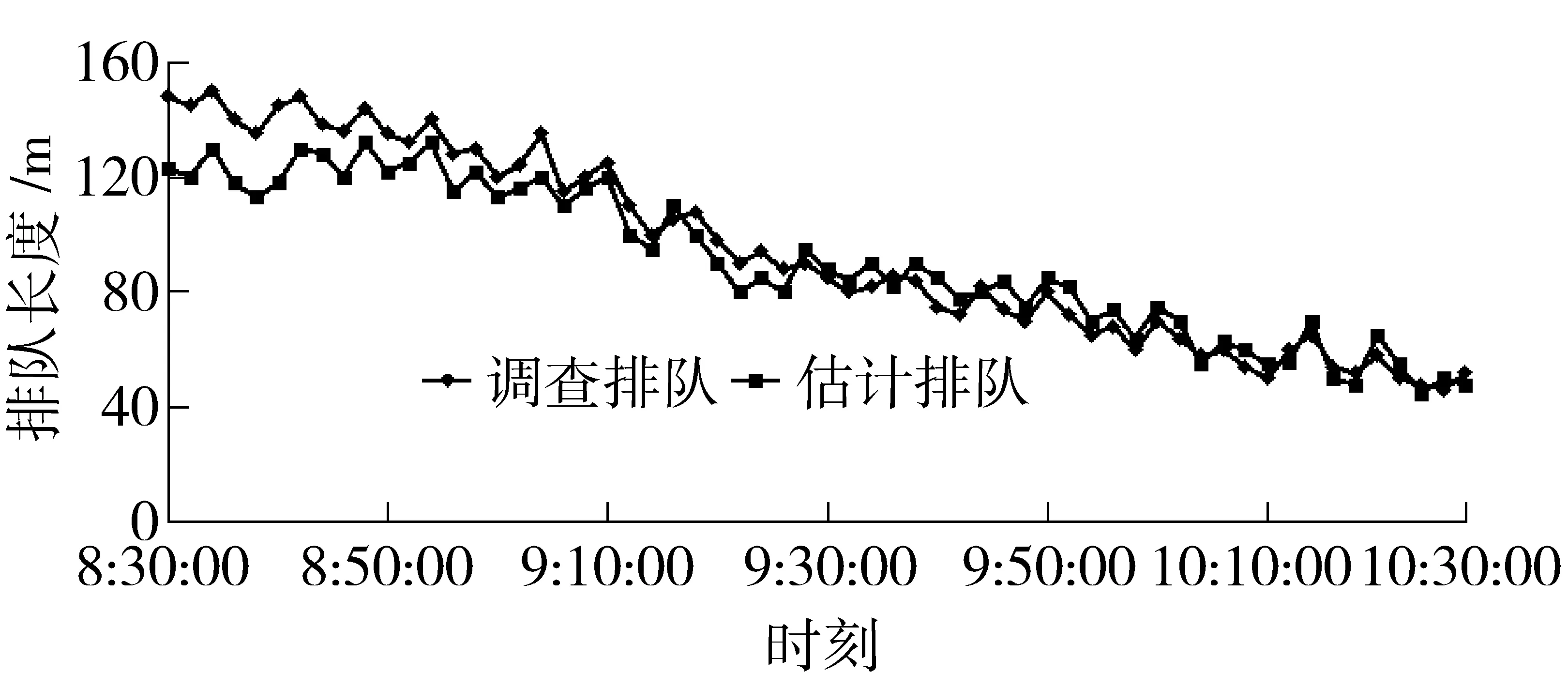
1) 欠饱和状态:Tdelay 2) 饱和状态:Tdelay>tred+β 3) 临界饱和状态:tred 其中,Tdelay为延误时间;β为机动车加减速损失时间常数;t1为机动车通过下游交叉口的实际时间;tn为机动车通过无灯控交叉口条件下的理论时间. 2.3 最大排队长度估计 交叉口排队长度是在确定交叉口交通状态后进行估计的,在不同的交通状态下估计方式不同. 根据交通状态判别方法,可得到通过交叉口的机动车排队次数公式 N=Tdelay/(tred+β)= (3) 交叉口处于欠饱和或者临界饱和状态下,即经过交叉口机动车停车次数N≤1,交叉口的周期最大排队长度分析如下: 图6 欠饱和状态下的交叉口排队长度估计 选取1个方向的2个相邻交叉口为例,以系统时间Time为横轴x,以路段长度Distance为纵轴y建立如图6所示排队长度估计示意图,通过视频检测系统可获得机动车通过上下游交叉口的时间,如图中不同机动车通过上游交叉口的时间分别为t′、t′1和t′2,对应通过下游交叉口的时间分别为t、t1和t2. 已知下游交叉口的红灯时间tred和绿灯时间tgreen,消散波速w2和机动车驶离速度um,可以确定线段HE和FD并相交于点E,机动车驶离上游交叉口的速度为ui,结合通过时间t′1可以确定机动车在路段上行驶的线段t′1B,BE为排队波与消散波之间平行于横轴的线段,其值为停车等待时间. 如果线段HE和线段t′1B与线段BE分别相交于2个不同的点,说明机动车在交叉口有停车排队. 如果2条线段相交于同一个点,说明机动车通过交叉口没有停车排队. 机动车在路段上的平均速度ui也可以通过视频检测系统获得,实现方式:上游交叉口设有视频检测器,不仅可以得到车辆通过交叉口的时间,也可得到通过交叉口出口车道断面的所有车辆数,该数据通过车牌信息获得,即路段交通流量. 依据格林希尔兹速度- 流量抛物线模型,可得到路段的平均速度ui,模型关系式: (4) 根据上述分析和已知条件,HE、FD、BE和t′1B所在直线可以分别表示如下: HE:y=-umx+umt1 (5) FD:y=w2x-w2tred (6) (7) t′1B:y=-uix+uit′1+l+d (8) 交叉口处于饱和状态下,机动车需经过多个信号周期才能通过交叉口,即机动车的停车次数N>1,以两次停车排队为例,机动车通过下游交叉口经历的过程如图7所示. 图7 饱和状态下的交叉口排队长度估计 在饱和状态下,机动车从上游交叉口行驶到下游交叉口的路段速度ui以及2次排队后驶离下游交叉口的速度um同欠饱和状态下的分析方法一致,区别是在机动车第1次排队启动后与第2次停车排队前的行驶状态. 如图7,D点为机动车第1次遇到排队波并停车排队位置,C点为第1次消散波到达时机动车启动行驶位置,uc为该机动车启动后并在2次排队前的行车速度,该值一般小于饱和交通流速um并可实测获得.B点为机动车遇到2次排队波并停车排队位置,在第2次消散波到达后机动车从A点启动行驶并以um通过下游交叉口.wc为2次排队的排队波速,此时机动车为均匀到达,可认为该值常数.wc计算公式 (9) 式中,qc为进口车道排队车辆;kc为进口车道排队车辆启动后的密度;该值可实测获得,kj为堵塞交通密度. 根据上述分析,可得出图7中相关直线可分别表示为: AD:y=-umx+umti AC:y=w2x-w2tred2 GH:y=wcx-wctgreen HE:y=-ucx+b IE:y=w2x-w2tred1 FB:y=-uix+uit′i+l+d 需要指出的是,无论是在欠饱和状态或是饱和状态下,交通流均具有波动性、随机性的特性,在上面的分析中,机动车的路段行驶速度是通过流量速度关系取得的,真实的数据一般不能完全匹配. 为此,在上面分析的基础上,如果满足如下约束条件,机动车i的停车位置即达到当前周期进口车道的最大排队长度: (10) 式中,|BE|为B点与E点的距离;α为路段延误常数;i为停车排队的机动车;di为机动车i停车位置到消散波直线FD(或IJ)的距离;d为队尾最后一辆机动车排队位置到消散波直线FD(或IJ)的距离. 本文研究实例选取北京望京地区望京北路与利泽西二路口为上游交叉口,自西至东到望京北路与广顺北大街交叉口为下游交叉口,数据调查日期为2014年2月3号,时间范围是8:30—10:30,并依据上述算法对调查数据对进行验证分析. 利泽西二路口东西向宽度d=50 m,两个交叉口相距l=340 m,几何平面信息如图8所示. 两个交叉口的信号配时如表2所示. 实例分析取值如下:qm=1 800 pcu/h,um=35 km/h,kj=182 pcu/km,km=80 pcu/km. 表2 信号配时表 s 根据提出的交通状态判别划分及相应状态下的最大排队长度估计方法,把选定的实际交叉口以及视频监测机动车的数据信息带入后,经过数据计算、整理与分析,最终得出选定时段的望京北路与广顺北大街交叉口西进口车道的周期最大排队长度数据. 把调查的排队长度和用本文方法所得的排队长度进行对比,得到如图9所示比较结果,图10为估计排队长度与实际数据的相对误差. 图8 实例路段几何信息 图9 调查与估计排队长度对比 图10 估计排队长度的相对误差 从图9可看出本文估计排队长度与实际排队长度折线是比较相近的,从图10的相对误差分析来看,相对误差在5%以内的比率为16.7%;5%~10%的比率为56.7%;10%~15%的比率为18.3%;超过15%的相对误差比率仅为8.3%. 其中最小和最大相对误差分别为2.44%和18.62%. 从数据分析来看,相对误差在可接受的范围内,估计的排队长度还是比较理想的. 另外,交叉口排队长度较长的相对误差相比排队较短的误差要大一些,说明在饱和交通状态下,本文提出的排队长度的估计方法还有待进一步研究以提高估计精度. 本文从交通管控和信息服务等对交叉口实时状态信息的需求出发,提出了基于视频数据的交叉口交通状态判别划分方法及最大排队长度估计,并进行了实例分析证明了本文方法的有效性. 首先,以现有的视频检测数据为数据基础、以集散波为理论支撑,处理得到机动车分别通过上下游相邻交叉口的时间和流量;然后通过分析交叉口延误对其交通状态进行判别,然后根据不同的交通状态对下游交叉口的最大排队长度进行了估计分析. 最后,通过实例对所提出的方法进行了验证分析,结果表明,在欠饱和状态下的估计排队长度较为理想,饱和状态下的估计精度还有待进一步提高. 下一步的工作,针对饱和交通状态下的排队长度估计精度、交通状态判别的发生概率以及如何通过交通信号优化改善交通状态并降低排队,将深入研究找出改进的方法. [1] 代磊磊, 姜桂艳, 裴玉龙. 饱和信号交叉口排队长度预测[J]. 吉林大学学报:工学版, 2008, 38(6): 1287-1290. [2] 王进, 白玉, 杨晓光. 关联信号交叉口排队长度计算模型[J]. 同济大学学报: 自然科学版, 2012, 40(11): 1634-1640. [3] 王殿海, 景春光, 曲昭伟. 交通波理论在交叉口交通流分析中的应用[J]. 中国公路学报, 2002, 15(1): 93-96. [4] 祁宏生, 王殿海. 信号控制交叉路口车辆排队长度[J]. 吉林大学学报: 工学版, 2009, 39(6): 1457-1462. [5] 荣建, 何民, 陈春妹. 信号交叉口排队长度动态计算方法研究[J]. 中国公路学报, 2002, 15(3): 101-107. [6] 何宁, 杨涛, 李朝阳, 等. 信号交叉口延误及排队长度的实证研究和应用[J]. 公路交通科技, 2002, 19(5): 106-109. [7] Comert G, Cetin M. Queue length estimationfrom probe vehicle location and the impacts of samplesize [J]. European Journal of Operational Research, 2009, 197(1): 196-202. [8] Ban X, Hao P, Sun Z. Real time queue lengthestimation for signalized intersections using traveltimes from mobile sensors [J]. TransportationResearch Part C: Emerging Technologies, 2011, 19(6): 1133-1156. [9] 庄立坚, 何兆成, 叶伟佳, 等. 基于浮动车数据的排队长度检测方法研究[J]. 交通运输系统工程与信息, 2013, 13(3): 78-84. [10] Michalopoulos P G, Pisharody V B. Derivation of delays based on improved macroscopic traffic models[J]. Transportation Research Part B: Methodological, 1981, 15(5): 299-317. [11] Newell G F. A simplified theory of kinematic waves in highway traffic, part Ⅰ: General theory. Transportation Research Part B: Methodological, 1993, 27(4): 281-287. State Discriminant and Queue Length Estimation of an Intersection Based on Video Data TANG Shao-hu, LIU Xiao-ming, CHEN Zhao-meng (North China University of Technology Beijng Key Lab of Urban Road Traffic Intelligent Tech., Beijing 100144,China) In order to estimate traffic states and periodic queue length evaluation of signal control intersection, this paper analyzed video detection data of vehicles by passing through adjacent intersections, proposed traffic state discriminant of an intersection based on the vehicles delay time, and developed the maximum queue length estimation method of an intersection in under-saturation or saturation traffic condition. The empirical analysis showed that the estimated queue length by the proposed method was closer to the actual investigation, and queuing relative error was in an acceptable range.The results validated that the designed method of queue length estimation of an intersection is feasible and effective. video data;traffic waves;traffic state discriminant; maximum queue length estimation 10.13986/j.cnki.jote.2015.01.011 2014- 11- 03. 国家自然科学基金(61374191), 国家高技术研究发展计划(863计划)(2012AA112401) . 唐少虎(1986—), 男, 博士研究生, 研究方向为交通控制. E-mail: tshaohu@163.com. U 491 A 1008-2522(2015)01-58-07




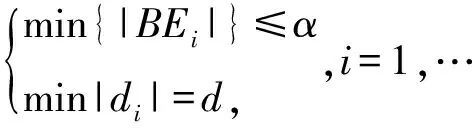
3 算法实例分析



4 结论
