基于路段变异系数的路径行程时间可靠度评价

刘 锴， 陈 晋， 龚节坤

(1.大连理工大学 交通运输学院， 大连 116024； 2.哈尔滨工业大学 交通科学与工程学院， 哈尔滨 150090)



基于路段变异系数的路径行程时间可靠度评价

刘 锴1， 陈 晋1， 龚节坤2

(1.大连理工大学 交通运输学院， 大连 116024； 2.哈尔滨工业大学 交通科学与工程学院， 哈尔滨 150090)

为了给出行者提供更准确的候选路径的行程时间可靠度，并克服缺乏完整观测样本的局限，介绍了一种符合对数正态分布假设和基于路段行程时间变异系数的路径行程时间可靠度评价方法，并解析了早到指数和迟到指数这2个符合概率特征的新指标. 分别在仿真的城市信号灯路网和乌鲁木齐市内环快速路开展实证研究，验证该方法在城市道路上的路径行程时间可靠度估计的适应性. 仿真结果证明，应用乌鲁木齐市少量浮动车数据的估计结果显示该方法简单实用，但是评价结果对各路段之间行程时间方差的差异程度较敏感，该方法易于夸大城市信控道路上的路径行程时间的不确定性.

路径行程时间可靠度; 变异系数; 早到指数; 迟到指数

出行者往往根据自己对路网和交通状况的经验选择出发时间、交通方式和出行路径，但是交通需求及交通状况条件受到很多无法预期的随机事件的影响，导致出行者可能做出错误的判断. 出行过程中的不确定性问题比单纯地减少出行时间显得更加重要，路径的出行时间可靠性成为出行决策的重要依据[1]，是交通管理者和出行者最关心的指标之一.

行程时间可靠度表示在规定的时间内，车辆从起点O到达讫点D的概率. 出行时间可靠度指标能反映行程时间的稳定性和预期时间内完成出行的可能性，目前国内研究主要集中在路段可靠性评价，路段可靠度信息对于出行者决策的帮助仍然较为有限. 出行者希望获取最佳几条路径的出行时间及其可靠度信息，然后根据个人出行需求和偏好作出选择，然而由于路径完整出行的样本量较少，难以获得有效的统计估计，也几乎无法应用传统可靠度指标评价路径的行程时间可靠度.

Kaparias等[2]提出了利用路段行程时间分布特征计算路径早到指数和迟到指数可靠度的估计方法，本文验证其用于城市信控路网，开展路径可靠度评价的可行性，为城市交通信息系统提供路网评价和分析的工具. 结合乌鲁木齐市浮动车系统采集数据，开展针对乌鲁木齐市城市快速路网可靠度实例评价. 本文介绍了早到指数和迟到指数可靠度指标的定义和计算方法；应用VISSIM仿真系统，计算城市信号控制路网中采用该方法评价路径可靠度的精确程度，比较了不同路径和路段变异系数关系假设条件下的路径可靠度估计差异；开展了乌鲁木齐市内环快速路行程时间可靠度的实证研究，并提出未来的研究方向.

1 路径行程时间可靠度指标

行程时间可靠度是路网可靠度的常用评价方法，Asakura等[3]于1991年首次提出了行程时间可靠度的概念，从早期“给定OD的一次出行在规定时间内完成的概率”和“符合出行者期望的行程时间增加即意味可靠度下降”[4]，到后来的“在一天的某个时段一次出行在给定时间内到达目的地的概率”，或者“在不同天同一时段或者同一天不同时段的行程时间的稳定性和可依赖性”[5]，行程时间可靠度越来越重视不确定性交通需求时空分布的影响.

目前常用的行程时间可靠性指标中包括缓冲时间指数、痛苦指数和变异系数[6]. 缓冲时间指数表示“出行者考虑到拥堵延误的变化而额外支出的出行时间的比例”，相对更能满足出行者的需求. 痛苦指数反映了消耗时间最长的一部分出行者对于道路条件的不满意程度. 变异系数采用行程时间算数平均值除以标准差的百分率来表示，以说明样本的分散程度，是衡量各观测值差异程度的一个统计量. 常用的路径出行时间可靠性指标往往假设路径时间服从正态分布，而且其包含的各路段之间的出行时间相互独立，然而现实情况并非如此[7]. Rakha等[8]指出用这些指标来评价路径可靠性时存在各种问题.

普通出行者往往对上述评价指标缺乏足够的理解. 考虑到出行者一般关心的是到达目的地的早晚程度，Kaparias等[2]提出了早到指数和迟到指数2个指标，这2个指标不仅可以转换成等价的旅行时间，而且应用与距离单位无关的变异系数值把路径可靠度和路段可靠度联系起来，利用路段观测样本直接估计路径可靠度成为可能.

1.1 路段行程时间可靠度

(1)

(2)

定义量纲为一的路段行程时间离散程度：

(3)

路段期望行程时间和方差简化为：

(4)

(5)

根据对数正态分布的数学性质，得到路段出行时间对应于1-α置信水平的置信区间是：{eu(l)-zα/2σ(l)，eu(l)+zα/2σ(l)}={t(l)α/2，t(l)1-α/2}.zα/2是在置信系数为α时的标准正态分布尾概率，这是包含t(l)的一个不对称的区间，表示在路段上可能的最大行程时间和最小行程时间. 此外，为了保证不同长度的路段之间可以相互比较，必须剔除平均出行时间对于度量的影响. 由此定义了2个可靠度指标，即早到指数rE(式(6))和晚到指数rL(式(7)). 早到指数用来度量路段早到可靠性，表示早于期望到达时间的概率. 迟到指数用来度量路段行程时间延误可靠性，表示晚于期望到达时间的概率.

(6)

(7)

将量纲为一的Tlog(l)代入以上2个公式，得到

(8)

(9)

rE(l)和rL(l)的取值范围都是[0，1]，值越接近1，表明行程时间的波动越小，可靠度越高；而如果取值越小，则实际行程时间远离平均时间，可靠度越低.α代表置信系数，通常取值0.05或者0.1，对应置信水平为0.95或者0.90.

1.2 路径行程时间可靠度

假定路径p包含n条路段li，由式(8)和(9)，路径行程时间的早到指数和迟到指数可以通过路径行程时间变化对数Tlog(p)表示出来。路径的平均行程时间可以通过把组成路径的路段行程时间简单加和得到，即

(10)

Rakha等[7]提出了依据组成路段的行程时间方差估计路径行程时间方差的5种办法，并以美国得克萨斯I- 35高速公路部分路段为例，证明当路径行程时间的变异系数是组成路径的所有路段变异系数的条件期望值时,其路径行程时间的估计方差最接近真实水平。

(11)

Kaparias等[2]给出符合上述条件期望值时路径的行程时间离散程度对数Tlog(p)与路段的行程时间离散程度对数Tlog(l)之间的关系(式(12))，一般条件下路径的行程时间离散程度对数则符合式(13)，路径p的行程时间早到可靠指数(式(14))和迟到可靠指数(式(15))为：

(12)

(13)

(14)

(15)

2 仿真计算与分析

浮动车数据被广泛用来计算各个路段的行程时间[9]. 应用VISSIM仿真系统建立简单城市路网，分别得到各路段和包含多个路段的路径行程时间的真值以及相应的浮动车观测数据，进而应用早到指数和迟到指数方法分别计算路段和路径的行程时间可靠度，验证利用路段的行程时间统计分布特征估计路径的行程时间可靠度的可行性.

2.1 仿真路网和仿真环境

利用VISSIM建立起的路网包含6个交叉口(图1). 东西向主干道为双向六车道，南北向次干道均为双向四车道，主要研究东西向主干道，总长度为4km，其中各路段的长度从左到右依次是600、800、1 000、700、900 m. 仿真中交通流量的设置分为3个等级：自由流、中间流和饱和流. 主干道在3个状态下的交通流量依次设置为500、1 000和1 500 pcu/h，次干道的流量依次设置为300、600和800 pcu/h. 浮动车比例设置为占总车辆数的5%. 交叉口信号配时设置了2种(见图2)，其中两端出入口处主干道有效绿灯时间稍长. 每次运行仿真3 900 s，舍弃前300 s，取300～3 900 s的数据记录观测，记录间隔为5 min，12个时间段.

图1 VISSIM仿真路网示意图

图2 交叉口信号配时示意图

2.2 路段行程时间可靠度计算

通过30次仿真，分别统计不同交通流量条件下各路段各时段的平均行程时间和方差，置信水平取0.95时，计算各路段的早到指数与迟到指数. 例如，饱和流条件(即主干道交通流量设置1 500 pcu/h，次干道交通流量设置800 pcu/h)下路段28各时段内的各交通状况参数和可靠性指标值见表1. 各时段平均行程时间虽然相差不大，但是由于受信号灯控制影响，行程时间的变动性较大，导致可靠度水平存在显著差异(时段2比时段1可靠度显著提高).

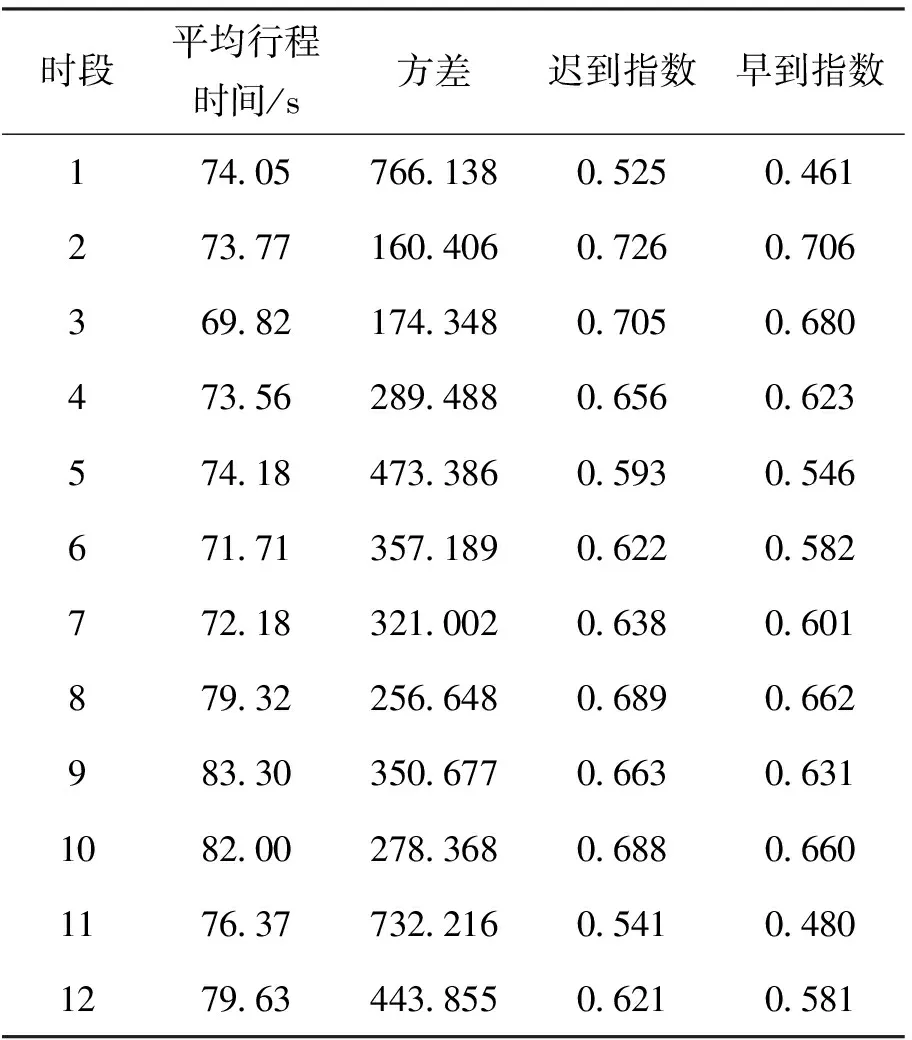
表1 饱和流下路段28的行程时间特征和可靠度

2.3 路径行程时间可靠度计算

设置路径1包含从左向右行驶的路段3、9、15、21、27，路径2包含从右向左行驶的路段28、22、16、10、4. 路径的入口和出口设置了行程时间的检测器，可以得到通过各路段(路径)车辆的行程时间真值，并计算基于行程时间真值的各路段和路径的实际行程时间可靠度(表2).

考虑到路段行程时间变异系数与路径行程时间变异系数的关系将影响利用路段方差计算路径可靠度的结果(Rakha等[7])，因此本文应用路段观测的行程时间信息估计路径的行程时间分布和可靠度，采用2种假设情况. 假设1: 路径变异系数为各组成路段变异系数之平均值；假设2：路径变异系数为各组成路段变异系数的中位数. 分别计算各路径的可靠度，结果见表3和表4.

比较表3和表4的行程时间可靠度真值与2种假设条件下的估计值，可见在该仿真路网和交通信号配时等条件下，估计结果高估了路径出行时间的不确定性，导致变异系数偏大，同时迟到/早到指数偏低. 但是当缺乏路径有效观测值而需要提供路径行程时间的可靠度估计时，该方法可行性较高，可以便利地给出较为准确的估计值. 比较2种假设条件，中位数假设情况下的路径1行程时间可靠度估计值更接近于真值，但是路径2的2种假设之间差距很小，平均数假设的估计结果更接近于真值.

表2 某时段的路径和路段行程时间和可靠度真值

表3 路径1行程时间可靠度真值和估计值

表4 路径2行程时间可靠度真值和估计值

3 乌鲁木齐行程时间可靠度计算

3.1 研究路径和数据

乌鲁木齐市城市现状布局为单核放射型，核心区位于城市南端，北段分别向东西两翼延伸，受用地限制，城市总体呈现向北发展态势，南部用地以居住、商业、办公为主，北部以工业、居住为主. 选择乌市的内环快速路(图3)作为研究对象，相比于普通的城市道路，快速路本身不存在平面交叉，不受其他方向交通流的影响.

将内环路主要分为6部分：BC、CD、DE、EF、FG、GB，由于FG部分数据量缺乏，所以不考虑该路段. 通过浮动车数据证实上述路段的行程时间分布与对数正态较为吻合. 研究顺时针和逆时针2个方向的2条路径，路径1：GB—BC—CD—DE—EF；路径2：FE—ED—DC—CB—BG. 利用路段上浮动车观测数据计算得到各路段行程时间以及变异系数等可靠度，再将这5条路段看作是组成内环路的基本路段，估计内环路顺时针和逆时针方向两条路径的可靠度.

图3 研究路径和组成路段示意图

3.2 路段行程时间可靠度

采用乌鲁木齐市6 000多辆安装有GPS定位仪的出租车作为浮动车，收集2013年11月的浮动车数据，记录周期为60 s，所运行路网基本涵盖所有乌鲁木齐市内主干道路网. 经过地图匹配对GPS点进行校准，利用校准后的点信息计算浮动车通过各个路段的行程时间. 统计各路段在不同时间段的行程时间均值和方差.

由于浮动车数据稳定性较差，数据丢失率较高，数据清洗后每个路段的有效观测样本量较少，难以考察该路径行程时间的日变和时变特征，因此仅考虑工作日和非工作日的差异，以及早晚高峰之间的差异，设定早上8:00—11:00为早高峰，晚高峰为18:00—22:00. 考虑0.95置信水平时的可靠度，表5列出了路段GB两个方向各时段的平均行程时间、方差以及变异系数、早到/迟到指数等行程时间可靠度指标.

3.3 路径可靠度

显然，由于几乎观测不到上述2条路径的完整出行样本，因此无法直接观测这种较长路径的可靠度. 采用上述2种路段的变异系数与路径变异系数的关系假设估计路径的行程时间可靠度. 表6和表7分别为路径1和路径2各时段内各基本路段行程时间的变异系数、平均值和中位数. 其中，只有路径2在工作日早高峰时段，由于个别路段(BG)的变异系数非常高，导致其平均值和中位数差异显著(见表7).

表5 路段GB的行程时间可靠度

表6 路径1各基本路段行程时间的变异系数

表7 路径2各基本路段行程时间的变异系数

*该路径的行程时间变异系数的平均值与中位数相差较大

在每个时段中选取构成路段变异系数的平均值和中位数作为路径行程时间的变异系数，计算出行程时间对数Tlog(p)，再计算路径在各个时段的可靠度(见表8).

表8 各路径在各时间段内行程时间可靠度

*路径在工作日早高峰时段，早到指数/迟到指数的平均值假设和中位数假设结果相差较大

早到/迟到指数反映了行程时间分布的两端(最短行程时间和最长行程时间)发生的概率，反映了行程时间分布的离散状态，因此，上述2条路径的早到指数和迟到指数变化趋势相同. 由于本研究数据限制，时段划分相对较长，难以考察时变特征，各路径各时段的早到/迟到指数差异并不十分显著. 2条路径的共性变化规律包括：周末早高峰可靠度高于工作日早高峰；2条路径的差异表现在：路径1中晚高峰时间段的可靠度都小于早高峰时段的可靠度，路径2工作日晚高峰时段可靠性较高，周末则早高峰时段可靠性较高.

由于BG路段的行程时间变异系数较大，导致采用2种假设时，估计的路径可靠度差异较大，其中中位数假设显然忽略了该路段的特殊情况，导致较高的可靠度评价，证明了乌鲁木齐城市快速路网的路径行程时间变异系数符合Rakha等[8]的结论，即当路径行程时间变异系数等于其组成各路段的行程时间变异系数的数学期望值时，路径行程时间的方差最接近实际水平.

4 结论

本文总结和介绍了路径行程时间可靠度评价的常见问题，并选取变异系数、早到指数和迟到指数作为可靠度评价指标进行路径可靠性评价. 相对于变异系数，早到指数和迟到指数这2个符合概率含义的指标更容易理解，反映了行程时间分布的两端(最短行程时间和最长行程时间)发生的概率，反映了行程时间分布的离散状态，应用路段行程时间变异系数和路径行程时间变异系数的假设关系，可以在缺少观测数据的情况下，给出较为合理的路径出行时间可靠度的估计值，并结合乌鲁木齐市内环路开展了有效的应用和评估，具有较好的推广价值.

由于本研究数据限制，时段划分相对较长，难以考察路段和路径行程时间可靠度的时变特征，今后进一步收集时空覆盖强度更广的数据，改进路径与其组成路段的行程时间变异系数的关系，开展应用路径早到/迟到可靠性指标的路径可靠度的时变特征分析.

[1] Noland R B, Small K A. Travel-time uncertainty, departure time choice, and the cost of morning commutes [J]. Transportation Research Record, 1995, 1493: 150-158.

[2] Kaparias I, Bell M G H, Belzner H. A New Measure of Travel Time Reliability for In-Vehicle Navigation Systems [J]. Journal of Intelligent Transportation Systems: Technology, Planning, and Operations, 2008, 12(4): 202-211.

[3] Bell M G H, Iida Y. Network reliability[A]. Bell, M. G. H. and Iida, Y.(eds. ) Transportation network analysis[C]. Chichester, UK: Wiley and Sons, 1997: 179-192.

[4] Al-Deek H, Emam E B. New methodology for estimating reliability in transportation networks with degraded link capacities [J]. Journal of Intelligent Transportation Systems, 2006, 10: 117-129.

[5] Lomax T, Schrank D, Turner S, Margiotta R. Selecting travel reliability measures[R]. 474360-1, Texas: Texas Transportation Institute, 2003.

[6] Noland R B, Polak J W. Travel time variability: a review of theoretical and empirical issues[J]. Transport Reviews, 2002, 22: 39-54.

[7] Rakha H, El-Shawarby I, Arafeh M, Dion F. Estimating path travel-time reliability[C]∥ITSC 2006, 9thInternational IEEE Conference on Intelligent Transportation Systems, Toronto, ON, Canada, 2006: 236-241.

[8] Rakha H, El-Shawarby I, Arafeh M. Trip Travel-Time Reliability: Issues and Proposed Solutions[J]. Journal of Intelligent Transportation Systems: Technology, Planning, and Operations, 2010, 14(4): 232-250.

[9] Chen K, Yu L, Guo J, Wen H. Characteristics analysis of road network reliability in Beijing based on the data logs from taxis[C/CD]. Proceedings of the 86thAnnual Meeting of the Transportation Research Board, Washington, D. C. USA: National Research Council, 2007.

Estimating Route Travel Time Reliability Based on Coefficient of Variation of Road Segments

LIU Kai1, CHEN Jin1, GONG Jie-kun2

(1.School of Transportation and Logistics, Dalian University of Technology, Dalian 116024, China;2.School of Transportation Science and Engineering, Harbin Institute of Technology, Harbin 150090, China)

In order to improve the trip travel time reliability (TTTR)estimation under small samples,this paper proposed a method for estimating the trip travel-time reliability using its component segments travel-time variance. Two new indexes:the earliness index and lateness index that conform to the characteristics of probability are analyzed. The flexibility of these two indexes is verified by using both a simulated signal controlled urban arterial network and the Urumqi inner ring network.Results indicated that this TTTR estimation method, as well as these indexes,are useful in field experimental analysis even with sparse probe data.The estimation is sensitive to the significant difference among the component segments’ and travel-time variance; and furthermore,the uncertainties of trip travel time in the signal controlled arterials may always be over-estimated.

trip travel time reliability; coefficient of variation; earliness index; lateness index

10.13986/j.cnki.jote.2015.01.001

2014- 12- 30.

教育部- 中国移动科研基金项目(MCM20122071)，教育部留学回国启动基金(第46批).

刘 锴(1978—)， 男， 副教授， 研究方向为交通行为建模和交通网络分析. E-mail: liukai@dlut.edu.cn.

U 491

A

1008-2522(2015)01-01-07