不停车通过待行区的交通信号精细化控制与优化

王大海， 王 茜

(1.北京汇海博科技发展有限公司， 北京 100022； 2.中国移动北京公司， 北京 100007)



不停车通过待行区的交通信号精细化控制与优化

王大海1， 王 茜2

(1.北京汇海博科技发展有限公司， 北京 100022； 2.中国移动北京公司， 北京 100007)

对于有待行区的交叉口，通过精细化设计信号控制，由路口停车线到二次停车线的距离sj和首车的最慢车速vej决定Tj；首车绿灯前进入时间如小于等于Tj，并以最慢车速vej行驶，可不停车直接通过待行区；消除2种放行时间损失，及减速停车再加速过程中的油耗损失、尾气污染和刹车噪声；改善环境空气质量. 还可把该路口纳入与相邻路口协调控制. 由最小绿灯时间组成的最小周期整幅配时方案出发，待行区不停车放行效益与周期的比值在所有绿灯前进入时间等于对应的Tj时达到最大，11层次数据例表明，待行区8个框架车流进口的有效放行时间总和相当于周期时长的3.7倍. 成倍提高了路口乃至城市地面路网通行能力. 相当于再建个地面路网.

待行区； 释放时间损失； 不停车； 通行能力； 改善空气质量

交通信号控制(Traffic Control，TC)系统已有上百年的历史，因机动化进程远超修路速度，交通伤害和拥堵广泛发生，尾气污染严重. 联合国大会[3]认为，应由TC系统的设计者负主要责任，而不是道路使用者. 设计者主要包括道路管理者、汽车行业、警察、政界人士和立法机构. 道路使用者仅负有遵纪守法的责任.

北京市大气污染防治条例规定“机动车驾驶员在停车3 min以上时，应当熄灭发动机”. 说明：1)机动车停车不熄灭发动机确实污染大气；2)存在TC方案某红灯时间超过3 min.

机动车待行区技术自2001年和2005年专利文献[4-5]公开，国内外虽已广泛应用，但尚存争议[6-7]. 2006年[8]就发现“设置待行区引起车辆平均停车次数增加，存在减速停车再加速过程中的油耗损失、尾气污染和刹车噪声”；且目前的停车待行存在待行区满载后至启动波传递到进口停止线之前的车辆不能进入的时间损失，及把同一进口车流断为2部分先后进入路口停车线，并隔断了相邻路口间协调控制.

如实施不停车通过待行区，则可消除上述弊端，发掘巨大通行能力，也强化协调控制.

1 待行区设置的基本理论

1.1 平面交叉口定理

不同交通流经过的共同区域为冲突区域，使平面交叉口成为地面交通路网的瓶颈，通过提高平面交叉口的通行能力将同步提高交通路网的通行能力.

路口各车流通行能力是通过其进口车道数和有效绿灯放行时间、绿信比来体现的，即：

Gej=Gj+A-l=Cλj

(1)

式中,Gej为车流j有效绿灯放行时间(s)；Gj为车流j绿灯时间(s)；l为绿灯损失时间(s)；C为周期(s)；λj=Gej/C，为绿信比.

文献[9-10]提出：行人和非机动车通行能力可通过拓宽其过路宽度而获得. 而机动车进口道数量则局限于路口四角建筑，故应重点关注存在机动车间冲突的车流，称为框架车流.

C=∑(Gi+Iij)

(2)

式中Iij是一股交通流i整幅放行绿灯结束时刻和下一股冲突交通流j整幅放行绿灯开始时刻的间隔，称为绿灯间隔时间. 在多相位方案中式(2)一般包含4个框架车流.

例1：如按英国实测，取绿灯损失时间为1.48 s，其中黄灯末损失时间为0.13 s[1]. 且传统十字路口控制方案，周期C=100 s，黄灯4 s，全红3 s，则Iij=7 s；在黄灯禁行时期，8个框架车流各进口有效放行时间总和仅达136 s；黄灯通行免罚后，也仅达168 s.

1.2 冲突区域不变定理

同一交通流存在多个冲突区域，通过设置二次停车线，可把冲突区域划分在前、后两侧：靠近出口的冲突区域称为线后冲突区域；靠近进口的冲突区域称为线前冲突区域. 二次停车线的位置虽影响冲突区域名称，但不改变冲突区域实际位置.

1.3 待行区可设置原理[4]

信号控制系统采用各进口“先直后左”的放行顺序，可使每个框架车流，在紧贴其整幅放行前一段时间内，其线前冲突区域上无其他交通流通行，可设置为该框架车流的待行区，在整幅放行之前进入，待出口放行时驶出.

1.4 清空定理

与行人安全岛不同，进入待行区所有车辆，皆须在出口放行期间出交叉口.

1.5 绿灯前进入待行区时间定理

待行区车流存在3种进入待行区时间：绿灯前进入时间、整幅放行绿灯时间和黄灯时间；传统绿灯初损失时间和黄灯末损失时间分属其首末.

2 二次停车线位置和待行区的5种信号灯信号组合

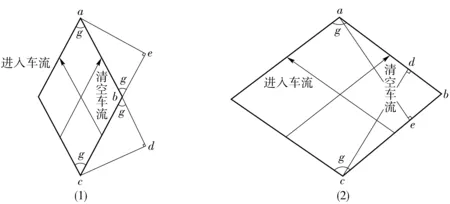
二次停车线位于待行区终点，需满足如下要求：①在待行区等待的车辆不得影响正在放行的交通流通行；②在满足①的前提下使路口停车线到二次停车线的最小距离min{sj}尽可能长；③尽可能使首车能以最大速度通过第1个线后冲突区域，占据冲突区域时间最短.

例2：对于待行区不停车而言，要求③可通过待行区首车驾驶员自动实现：根据出口红灯倒计时信息和距离，可自主控制车速，恰好在允许通行时，不停车越过二次停车线.

显示车辆越过二次停车线的路权也需信号灯信号，但只需2种灯色：红灯停，绿灯行，不需黄灯. 为区分不同流向的出口信号灯，须附箭头指示，如图1. 初次使用时，须公示.

设置了出口信号灯组后，原整幅信号灯组的红、绿、黄信号功能就转变为显示车辆越过路口停车线路权的进口信号. 此设置可有5种实用信号组合，其放行顺序和路权含义如下：

1) 进口绿灯，出口红灯：允许车辆越过路口停车线，但不允许越过二次停车线；

2) 进、出口绿灯都亮：相当于整幅放行绿灯，既允许车辆越过路口停车线，也允许越过二次停车线；

3) 进口黄灯，出口绿灯：相当于传统整幅放行黄灯，表示禁止通行的红灯将亮，既允许车辆越过路口停车线，也允许越过二次停车线；

4) 进口红灯，出口绿灯：相当于传统整幅放行红灯，表示禁止通行，不允许车辆越过路口停车线；但已在待行区的车辆可优先通行，其他车辆应礼让；

5) 进、出口红灯都亮：相当于整幅放行红灯，禁止通行，不允许车辆越过路口停车线和二次停车线；该信号组合只能在待行区车辆已全部出走后出现.

设置出口红灯倒计时，提示待行区首车驾驶员到达二次停车线的时间，方便其自主控制车速，恰在出口绿灯开始时不停车越过二次停车线；也改善越过二次停车线的饱和度.

设置进口黄灯倒计时，帮助尚未越过进口停车线的驾驶员准确判断，自己是否能在红灯之前安全越过进口停车线，如不能就必须在进口停车线之前顺次及时停车，闯红灯必罚.

各倒计时只显示个位，留有时间方便动态修改变动控制方案的控制参数.

3 关键点和最短绿灯间隔时间

用文献[9-10]方法可使待行区车道数成倍大于进口车道数. 如图1.

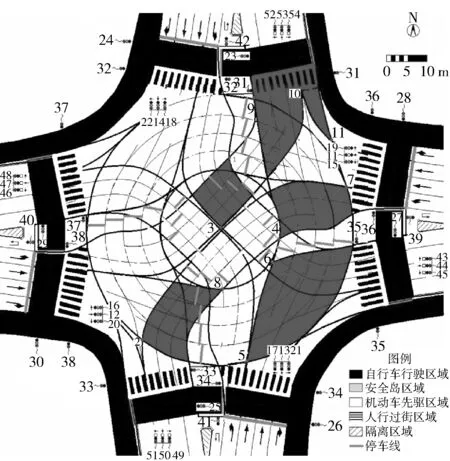
图1 一种平面十字交叉口的最优渠化方案

关键点为同一冲突区域中对于同一放行顺序最易发生冲突的点. 文献[9-10]提出：

存在性定理：在保安全的前提下，Iij必存在最短值Imij，称为最短绿灯间隔时间.

3.1 最短绿灯间隔时间定理

清空始于红灯初. 在“灯头让行灯尾”的法律下，有

Imij=A+max{tci}-min{tej}

(3)

式中：A为黄灯时间(s)；tci为绿灯i尾车通过清空距离所用时间(s)；清空距离为绿灯i尾车从其停止线越过关键点所走距离(m)；max{tci}为tci累积分布函数的85%位值(s)；tej为绿灯j首车通过进入距离所用时间(s)；进入距离为绿灯j首车从其停止线到达关键点所走距离 (m)；min{tej}为tej累积分布函数的15%位值(s). max{tci}与min{tej}分别对应车速累积分布函数统计数据min{vci}与max{vej}，可测.

此定理明确：式(3)的Imij能且必能实现：即使整幅绿灯i尾车在黄灯末时刻越过停车线，并以速度min{vci}前进，也能在整幅绿灯j首车以速度max{vej}到达关键点之前，安全越过关键点. 即使偶尔出现极端情况，“灯头让行灯尾”者也不会久等.

3.2 线后关键点进入距离定理

式(3)对于设置待行区的路口依然成立. 二次停车线后关键点的进入距离从二次停车线起算，清空距离从进口停车线起算.

根据文献[9-10]提出的最短绿灯间隔时间计算定理，有关键点定理：关键点处的最短绿灯间隔时间Imij最大.

3.3 推论

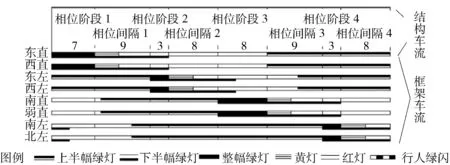
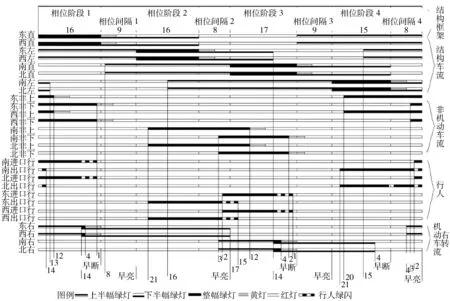
对于冲突区域的汇合角g，和实际运行车辆的车速累积分布函数统计数据的最小清空速度min{vci}与最大进入速度max{vej}：如min{vci}

4 待行区可不停车定理

4.1 待行区可不停车定理

设计信号控制方案，可由min{sj}和首车现实可实现的最慢车速的平均值vej确定穿越时间Tj=min{sj}/vej，j=1,2,…,8,对应各框架车流；如绿灯前进入时间小于等于Tj，首车以最慢车速平均值vej行驶，必可在放行期间不停车通过二次停车线.

图2 交叉区域的关键点

例3：待行区首车因二次停车线可能停车，并存在灯头让行灯尾的任务，可合理取加速度aej=2 m/s2，速度vej=1.5 m/s(即5.4 km/h)，为安全取max{vej}=2 m/s(即7.2 km/h).

低速的首车更能集中精力安全礼让各种尾单元，使行人和非机动车更安全.

按图1渠化，首车速度1.5 m/s，左转待行区最小长度60 m，Tj=60/1.5=40 s，直行待行区最小长度48 m，Tj=48/1.5=32 s.

故进入待行区的首车加速时间t0=vej/aej=1 s；加速距离s0=vejt0/2=1 m，sej小于s0的min{tej}=s1/2，sej大于s0的min{tej}=0.5+sej/2. 清空速度可记为：min{vci}=15 m/s(即54 km/h)，略小于路段最高限速16.7 m/s(即60 km/h).

存在停车时，出待行区的首车由二次停车线开始加速，如出口无堵塞，加速度可达5 m/s2，max{vej}=15 m/s，几乎等于清空车速. 加速时间t0=3 s；加速距离s0=22.5 m，当sej小于s0的min{tej}=(10 s)1/2/5，sej大于s0的min{tej}=1.5+sej/15.

统一取：非机动车速vnj=4 m/s/h，快速行人速度vpi=1.5 m/s，黄灯时间A=4 s. 有行闪=4 s.

即使未达到max{vej}，遵循公式(3)，取max{vej}=15 m/s，绿灯间隔也最安全，从而有进入时间min{tej}=sej/15. 设车辆皆为标准小汽车，车长6 m，(其他车型可用折减系数换算).

注意到进入待行区的最大进入速度与离开待行区穿越二次停车线的最大速度可能存在的巨大差异，从而根据上面的推论，使二次停车线前后冲突区域的关键点位置完全不同.

4.2 关键点位置可变定理

二次停车线前后冲突区域的关键点位置可因进入待行区的进入速度取值的巨大差异而完全不同. 相对各关键点的清空距离和进入距离也因此不同.

例4：因max{vej}约为0.13min{vci}，且图1中作为线前冲突区域的关键点1、2、3、7的汇合角都是钝角，远大于临界角，故位于进入首单元外侧最前端进入冲突区域处的b点，关键点5、11的汇合角小于临界角82.3度，故位于交通流内侧汇合处的c点；而作为线后冲突区域的关键点4、6、8、9、10、12，因进入速度与清空速度相近，则皆位于进入首单元外侧最前端进入冲突区域处的b点. 如图1灰色区域中点1～12所示.

基于上述参数，据图1路口渠化比例，可得各最短绿灯间隔时间.

文献[9-10]提出了缩小周期损失时间的4个互补技术，与待行区相互兼容，故完全可继承和发展、应用.

分道提速定理：利用路口内空间资源，使待行区车道数大于对应进口车道数，因分道后续车辆在进口处车速与饱和流量高于前车，可由首车的低速自然逐步提高至最高的清空车速，极大地提高了在进口处的车速与饱和流量，降低了绿初损失时间，提高了路口放行能力.

例5：后续车辆不担心其他车辆、非机动车和行人干扰，无让行问题；分道使车辆越过路口停车线的时间距也逐渐缩小，若前7个分别为6.1、4.9、4.0、3.2、2.6、2.2、2.0 s/pcu，则绿灯初损失时间为11 s. 待行区放行23 s后达正常饱和流率.

5 待行区最大放行效益定理

无待行区的放行方案仅是不停车通过待行区方案的一特例：首车以正常速度行驶. 较无待行区而言，待行区所增的放行效益就体现在首车可实施慢速行驶的程度上；首车取合理最慢车速vej可增待行区最大放行效益.

此定理意义在于使待行区与无待行区方案的放行能力具有了可比参量和优化方向.

例6：应用文献[9-10]技术，可寻找由最小绿灯时间组成的最小周期整幅配时框架方案.

各车流最小绿灯时间{Gmi}：东直Gm1=7 s、西左Gm2=3 s、北直Gm3=8 s、南左Gm4=3 s、西直Gm5=7 s、东左Gm6=3 s、南直Gm7=8 s、北左Gm8=3 s. 最小相容组合{Iij}：I1=9 s、I2=8 s、I2′=8 s、I3=9 s、I4=8 s、I4′=8 s、I5=9 s、I6=8 s、I6′=8 s、I7=9 s、I8=8 s、I8′=8 s.

则不同整幅周期链的链长皆为55 s，定为周期. 各相位阶段时间：7、3、8、3 s；相位间隔时间：9、8、9、8 s；如图3. 因车辆越过路口停车线后再越过二次停车线，需一定行驶时间. 出口绿灯须亮到冲突车流首车通过线后的关键点. 绝不能因信号错误把车辆拦在待行区内.

图3 图1交叉口周期55 s的信号组- 时间序列图

6 待行区的最大绿灯前可进入时间与绿灯初损失时间

绿灯配时可改变绿前可进入时间定理：影响绿灯前可进入时间的主要是前冲突框架车流绿灯迟断(早断)时间、最短绿灯间隔时间和累积相位间隔时间，并由之影响各前冲突非机动车和行人绿灯时间的扩大. 绿灯配时可改变累积相位间隔时间，从而改变绿前可进入时间.

例7：如文献[9-10]，利用绿灯间隔，可计算图3中各框架车流的最大绿灯前可进入时间. 左转车可提前31 s进入待行区，差9 s不到40 s；东、西直行车可提前20 s进入待行区，差12 s不到32 s. 南、北直行车可提前19 s进入待行区，差13 s不到32 s. 可不停车通过.

在红灯倒计时的提示下，诱导待行区首车驾驶员，根据有限的距离和时间，可自愿且自主控制车速约为1.5 m/s，并适时加速；在出口绿灯亮起时刻，恰好到达二次停车线，实现不停车通过.

例8：注意到传统“黄灯禁行”期间周期小于100 s的无待行区方案的每周期各框架车流的有效放行时间总和仅相当于1.5个周期，“黄灯允行”后比值升为1.8. 而本待行区不停车最小绿时方案为2×[(20-11)+7+4+(31-11)+3+4]+2×[(19-11)+8+4+(31-11)+3+4]=188 s，相当于周期55 s的3.4倍. 与例1比，为其多出的放行能力就是待行区放行效益.

7 不停车优化效果的数据例题

不停车优化定理：如各待行区容量足够大，可优化筛选信号控制系统诸多参数：如由最小绿灯时间组成的最小周期整幅配时框架方案的某些绿前可进入时间不能达到穿越时间Tj，通过增加某直行绿灯时间可等量增加对向左转的绿前可进入时间和周期长度，通过增加某左转绿灯时间可等量增加左侧进口直行的绿前可进入时间及周期长度，也增加待行区放行效益与周期的比值；如某些绿前可进入时间超过对应穿越时间Tj，可延迟进入时间到等于Tj，确保首车能不停车通过二次停车线；此延迟不能缩小周期长度；如所有绿前可进入时间都已等于对应的穿越时间Tj，则每周期待行区不停车效益已最大，再增周期长度就会降低待行区不停车效益与周期长度的比值；在不停车通过各待行区的前提下，进一步优化筛选诸多参数，包括最小相容组合参数等，使待行区放行效益/周期的比值最大.

例9：因图3由最小绿灯时间组成的最小周期整幅配时框架方案的各绿前可进入时间皆不能达到Tj，故可适当增大绿灯时间，使各车流绿灯时间{Gi}分别为：东直G1=16 s、西左G2=16 s、北直G3=17 s、南左G4=15 s、西直G5=16 s、东左G6=16 s、南直G7=17 s、北左G8=15 s. 使直行各绿前进入时间皆为32 s，左转提前进入时间皆为40 s，皆达到对应的Tj；周期达到98 s. 配时框架方案如图4.

图4 图1交叉口周期98 s的框架车流信号组- 时间序列图

例10：增加绿前进入时间，需验证待行区动态容量，不能溢出. 查各pcu动态空间距若平均12 m，则左转待行区3车道可容纳14个pcu；直行待行区4车道可容纳16个pcu；大于可进入量，确无溢出.

例11：除去待行区放行的绿初损失时间11 s，每周期待行区框架车流各进口的有效放行时间总和可达2×[(32-11)+16+4+(40-11)+16+4]+2×[(32-11)+17+4+(40-11)+15+4]=360 s，相当于周期98 s的3.7倍. 与例1比，提高通行能力1倍多.

8 结论

本文应用文献[9-10]的精细化技术，拓展了待行区技术的图1渠化极限长度和车道数.

1) 不仅消除了文献[6]所述待行区的种种弊端，而且发掘出待行区技术具有的巨大放行效益，可改善、推广待行区技术.

2) 通过11层次数据例，结合首车驾驶员和合理的极限低速，明确了极限绿前可进入时间，证实了不停车优化定理和最大放行效益定理.

3) 不停车通过待行区，有助避免交通伤害、缓解交通拥堵和尾气、噪声污染；可登峰造极，成倍增加路口乃至路网通行能力和放行效率，相当于再建个城市地面路网.

认识世界的目的是改造世界. 每周期的首车合理最低速的待行区不停车技术经济效益巨大，应用需求迫切，推广前景广阔. 已经申请专利，具有中国完全自主知识产权[5，9]. 性价比高，绿色环保可持续；时间和空间资源的浪费是不可弥补的，应抢先推广、应用.

[1] 吴兵, 李晔. 交通管理与控制[M]. 北京: 人民交通出版社, 2009.

[2] 全永燊, 城市交通控制[M]. 北京: 人民交通出版社, 1989.

[3] 2011—2020年道路安全行动十年全球计划. 联合国大会在2010年3月通过的A/RES/64/255号决议[EB/OL]. http:∥www.who.int/roadsafety/decade_of_action/zh/.

[4] 王茜, 王大海. 按半幅路权进行路口交通流分离的方法和交通信号机[P]. CN201010103079. 2.

[5] 王大海. 多相位平面交叉路口的交通信号控制系统(已获权)[P]. ZL 200520011383. 9.

[6] 王殿海, 李丽丽, 陈永恒. 机动车左弯待转区设置的临界条件[J]. 公路交通科技, 2009, 26(11): 132-135.

[7] 宗二凯, 邵长桥. 设有待行区的左转车道通行能力计算方法研究[J]. 武汉理工大学学报, 2011, 33(10): 64-68.

[8] 倪颖, 李克平, 徐洪峰. 信号交叉口机动车左转待行区的设置研究[J]. 交通与运输, 2006(B12): 32-36.

[9] 王大海, 王茜. 可具有负系统损失时间的动态信号控制系统的控制方法[P]. 专利申请优先权文件101010103079. 2；交通信号控制系统、设计方法和特殊设备, 国际专利[P], 申请号PCT/CN2011/070879.

[10] 王大海, 王茜. 周期损失时间L进入负值的精细化最优自适应交通信号控制[A]. 第九届中国智能交通年会学术委员会. 第九届中国智能交通年会优秀论文集[C], 北京: 电子工业出版社, 2014: 191-200.

Optimization of the Traffic Signal Fine Control for Passing Through the Waiting Area Without Any Stop

WANG Da-hai1， WANG Qian2

(1.Beijing HHB Sci.& Tech Co. Ltd., Beijing 100022； 2.China Mobile Group Beijing Co. Ltd., Beijing 100007)

For the intersection with waiting areas,Tjjcan be calculated based on the distancesnfrom the stop line to the second stop line, and the first slowest bus speedvej; if the first bus enters the intersection at mostTjbefore the next green and runs at the slowest speedvej, it will be able to go through the waiting area without any stop; this would eliminate the two types of starting time loss,reduce fuel consumption and brake noise, and improve the air quality; And the intersection with waiting area can be interconnected with the adjacent intersections to facilitate progression, and this will increase intersection capacity. Based on the empirical data analysis,the ratio of the waiting area without stop benefit to the cycle reaches the maximum when the first bus enters the intersectionTjbefore the beginning of the next green. Further analyses show that, the sum of the effective release time of waiting area for eight frame works of traffic is 3.86 times the cycle length. This new method is proven to increase the capacity of the intersection significantly.

waiting area； release time loss； no stop； traffic capacity； improved air quality

10.13986/j.cnki.jote.2015.01.010

2014- 10- 13.

王大海(1948—)，男，研究员，研究方向为交通信号控制的优化和自适应. E-mail:Wang6dh@163.com.

U 491.9+2； U 491.2+65

A

1008-2522(2015)01-52-06