可变限速控制下的城市快速路交通流混沌分析*
2015-04-13陈淑燕
谷 健 陈淑燕▲
(1.东南大学城市智能交通江苏省重点实验室 南京210096;2.东南大学现代城市交通技术江苏高校协同创新中心 南京210096)
0 引 言
在混沌系统中,初始条件的较小波动将导致结果较大的扰动,从而削弱系统的稳定性。交通流系统作为一类复杂的动态系统,通过分析交通流时间序列,能够在交通运行过程中识别混沌特征的存在,如J.E.Disbro[1],D.S.Dendrinos[2],X.Y.Zhang[3],T.Li[4],P.J.Shang[5]等人对此进行了深入研究。混沌特征会给交通流系统带来潜在的不稳定性,影响交通安全。因此,对于交通流混沌的控制成为热点,具体措施有很多,如可变限速控制。可变限速(variable speed limit,VSL)主要对车辆速度进行诱导与控制,从而改善速度离散性,维持交通流的稳定运行,达到减轻驾驶压力、提高道路交通安全的目的。在德国,VSL的应用表明道路通行能力提高了5%,交通事故数降低了37%;在英国,VSL的实施使得交通事故数减少了30%,二次事故也降低了40%左右[6-7]。VSL的实施不仅能够改善交通安全状况,对交通流的影响也以M.Parageorgiou等[8]为代表进行了研究。
VSL的实施从微观角度看会改变车辆行驶速度,从宏观角度看会改变交通流速度特征。在宏观交通流角度,对于可变限速实施效果的评价已有很多研究,但多基于传统交通流理论方法,缺少涉及交通流非线性特征、混沌特征等方面的效果分析研究;在微观角度,驾驶员在车辆驾驶过程中会对可变限速信息作出不同反应,学者们主要借助驾驶模拟器对不同情景下的驾驶行为进行研究,但这类研究更多关注个体,缺少从宏观角度考虑交通流特征的变化,需要进一步研究。
基于此,笔者通过设定交通流中遵循可变限速值的车辆数比例这一参数,忽略驾驶员行为的决策过程,转而从决策结果角度出发,利用成熟的时间序列非线性特征识别方法,分析研究可变限速策略作用下的交通流混沌特征,即重点探讨快速路基本路段车流中遵循可变限速值的车辆数比例与交通流速度时间序列混沌特征之间的关系,通过设定不同的比例构建仿真情景,在Vissim仿真环境下利用真实数据重建交通场景获得仿真数据,利用时间序列混沌特征识别方法,分析研究不同假设情景下的交通流速度时间序列混沌特征,并分析二者之间的关系,从交通流非线性特征角度为制定合理的可变限速值提供依据与参考。
1 时间序列混沌特征识别
对于简单的动力学系统,可以通过建立动力学方程来研究各变量的变化,但对于复杂系统,如交通流系统,建立明确的动力学方程比较困难,为此可通过观测交通参数的时间序列来判断交通流系统的混沌特性。
时间序列的混沌特性可用最大Lyapunov指数表征,一般用λmax表示。计算Lyapunov指数主要有Wolf法、小数据量法等。考虑到一般计算最大Lyapunov指数需要大于1 500的样本[9],而一般交通道路采集数据间隔为2min,1h为30个数据,数据量较小,为此选用小数据量法来计算最大Lyapunov指数。小数据量算法的核心,是首先寻找时间每个相点Xj的最邻近点Xη(j),最小距离如式(1)所示,其中Z为序列的平均周期,‖·‖为二范数。

之后依次计算每个临近点对在i个离散时间步长后的距离,如式(2)所示。

最大Lyapunov指数可通过估计每个相点与其最近邻点在轨道上的平均发散速度得到,如式(3)所示。式中:Δt为时间序列的样本周期[10]。
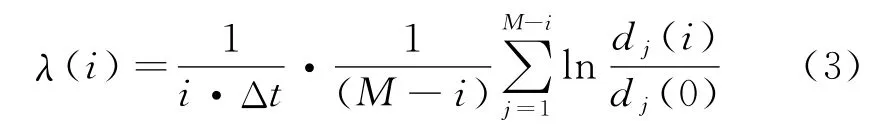
重构时间序列相空间是计算最大Lyapunov指数的基础,因此需要选择合适的时间延迟τ和嵌入维数m,以确定式(3)中的M,相空间中的相点数:M=N-(m-1)·τ。式中:N为时间序列长度。
目前对于这2个参数的选取方法大致分为两大类:一类认为2个参数之间互不相关,需要独立选取,此时选用的方法有序相关法、相空间扩展法等;一类是认为2个参数是相关的,参数的选取是相互依赖的,此时选用的方法有时间窗口法、C-C法等[9]。其中,C-C法基于BDS统计结论,利用关联积分计算得到最优时间延迟τ和嵌入窗宽τw=(m-1)·τ,从而同时得到时间延迟和嵌入维数的估计值[11]。以下分析将选用C-C法重构时间序列相空间。
2 实例分析
2.1 案例分析区域
选用北京市三环快速路(外环方向)紫竹桥可变限速标识上下游路段作为仿真场景,路段包含3处RTMS检测器断面,检测器编号分别为3051,3050,3049,1处可变信息标识,以及2处入口匝道,空间位置如图1所示。其中,可变限速标识VSL处于检测器3050和3049之间,构建仿真场景依赖于真实检测器数据,具体为统计间隔为2min,时长1个月内05:00~23:00时之间的RTMS统计数据,包括分车道断面交通流量、速度、占有率。另外在Vissim仿真中通过设置数据采集器模拟RTMS采集的功能。
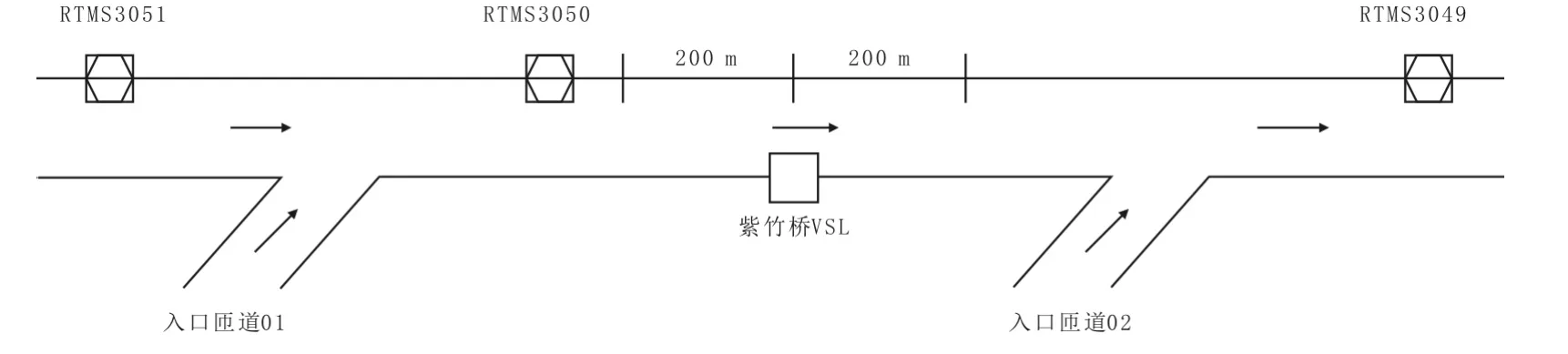
图1 北京市3环快速路紫竹桥路段外环方向(RTMS3051-RTMS3049)Fig.1 Zizhuqiao section from RTMS3051-RTMS3049on 3rd expressway in Beijing
2.2 仿真参数设定
针对本次案例分析,Vissim仿真中主要设定交通流特性参数与驾驶行为参数,对于驾驶行为参数,主要参考文献[12]中设定的驾驶行为参数值。另外,为避免车型带来的影响在Vissim仿真中车型仅选择“car”类型。
1)速度参数设定。本次应用中速度参数的设定主要从车辆速度构成与可变限速值2个角度出发。其中,利用统计间隔为2min的RTMS速度数据提取速度特征,基于此作为Vissim速度参数输入。另外,通过设置期望速度决策模拟可变限速功能,在实际操作时,结合数据质量,简化可变限速值的确定过程,以1h为统计周期,以15%速度作为最低限速值、85%速度作为最高限速设置每小时的期望速度决策值,具体见表1。

表1 VSL速度限值(05:00~23:00时)Tab.1 VSL value during 05:00~23:00in one day km/h
2)流量参数设定。交通流特性参数除了设定车速参数,还需要设定路段入口流量参数。考虑到本次所选用的匝道流量数据质量较差,因此利用估计方法得到入口匝道流量。针对本次案例分析,设定如下前提:在单一交通流方向,忽略“回头车”,路段上游不会“吸引”从下游路段驶入的车辆,即车辆通过入口匝道驶入快速路,通过出口匝道驶出快速路。同时,考虑到替代路径的存在,假设从入口匝道驶入的车辆,不会从距离间隔较小的出口匝道驶出。基于此前提,可将流量估计简化成线性问题,即如图1所示仿真区域中RTMS3051断面、入口匝道01断面、RTMS3050断面之间距离较短,某一时段内断面之间的主路车辆数可用式(4)近似估计。

式中:Nin为某一时段内入口断面通过车辆数;Nout为某一时段内出口断面通过车辆数。
同理,借助断面之间的距离及平均车长[13]对式(4)进行修正,得到式(5)对RTMS3050断面、入口匝道02断面、RTMS3049断面之间的主路车辆数近似估计。

式中:Nin与Nout与式(4)含义相同;Lin-out为主路上游入口断面到主路下游出口断面之间的距离,L-veh为某一时段内主路路段中的平均车长。
具体操作时,以RTMS3051、入口匝道01断面为入口断面,RTMS3050断面为出口断面,利用RTMS采集到的小时流量,利用式(4)对入口匝道01的断面交通流量进行估计,同理利用RTMS3050,RTMS3049采集到的小时流量,利用式(5)估计得到入口匝道02的断面小时流量,结果见表2。

表2 小时交通量估计结果Tab.2 Hourly volume estimation veh/h
基于上述假设得到的流量估计结果需要检验。在此借助分析流量的GEH统计值校验断面的仿真值与实际值之间的差别[13],确定估计结果是否合理。
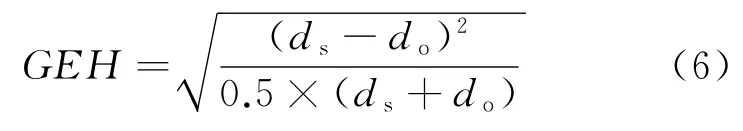
式中:ds为仿真数据;do为实际数据。
当GEH<5:较好拟合,仿真数据可用。
5<GEH<10:仿真参数需要校正。
10<GEH:拟合效果不好,仿真数据不可用。
根据式(6)计算得到仿真交通量的GEH统计值,见表3,计算得到的GEH值均小于5,结合文献[13],认为流量仿真数据是可用的。

表3 仿真区域交通流量GEH值Tab.3 GEHresults for tested basic expressway segments
2.3 仿真数据分析
1)交通流混沌特征识别。在图1中,与可变限速标识邻近的上下游RTMS检测器的距离均大于200m,根据相关文献,在下游200m之后能够检测到速度的变化[15],为提取到速度的变化特征,在Vissim中,以可变限速标识为起点,向上游延伸200m,向下游延伸300m,针对每条车道每隔50m设置数据采集器,采集断面交通流速度时间序列数据。
(1)没有实施可变限速策略时速度时间序列混沌特征。利用表2所列小时流量估计结果进行仿真,采集得到可变限速标识上游200m、可变限速标识位置断面及可变限速标识下游200m位置断面的速度时间序列。
以RTMS3051断面采集的速度参数时间序列为例,利用G-P算法计算关联积分C(r)及关联维D(m),如图2所示,随着m的增加D(m)趋于收敛,表明混沌特征存在。

图2 G-P算法计算关联维及嵌入维数Fig.2 Calculate correlation dimension and mby G-P algorithm
重构速度时间序列相空间并计算最大Lyapunov指数、λmax。计算结果见表4。由表4可见,6个位置对应的交通流速度时间序列对应的λmax均大于0。

表4 C-C法估计结果与λmaxTab.4 C-C method result andλmax
(2)实施可变限速策略时速度时间序列混沌特征。可变限速信息会改变交通流中车辆的行驶状态,假设此时交通流由两部分车辆组成,分别是按照可变限速值行驶的车辆和没有按照可变限速值行驶的车辆,并且假设车辆对可变限速信息的服从遵守程度是固定的,不随时间发生变化,直至离开研究区域。用参数p代表交通流中按照限速值行驶车辆的比例,并提出3种假设情景,分别为情景1(交通流中25%的车辆按照可变限速值行驶,S1,p=25%)、情景2(交通流中50%的车辆按照可变限速值行驶,S2,p=50%)、情景3(交通流中75%的车辆按照可变限速值行驶,S3,p=75%)。针对3种情景利用表2所列OD交通量,进行仿真得到断面速度时间序列数据,3种情景下对应3处断面位置的速度变化情况见图3。

图3 3种情景速度变化特征及比较Fig.3 Speed variation in 3scenarios and comparison
分析图3(a),(b),(c)可知,车流经过可变限速位置后,在下游200m位置处的速度均小于上游200m和可变限速位置的速度值;在相同位置处,如下游200m位置处,如图3(d)所示,S1情景下对应的速度要高于S2,S3情景下对应的速度值最低,接近最低限速值。
分别计算3种情景下的λmax,结果见表5。由表5可见,3种情景下3处断面位置的交通流速度时间序列对应的λmax仍大于0,混沌特征存在。
(2)p与λmax的关系。为进一步研究p与λmax之间的关系,以5%为步长,计算得到p∈[5 %,95%]下游200m位置的λmax,结果见图4。分析图4(a)可知,λmax与p之间存在负相关线性关系,即当交通流中的车辆按照某一速度行驶时,λmax趋于0,交通流状态趋于稳定,但这与所有车辆均按照同一速度行驶的现实存在差异,因此选用二次方程进行拟合,结果见图4(b)。与线性关系相比,二次函数形式存在合理的最小值,即当交通流中存在60%~80%车辆按照同一速度行进时,λmax趋于0,交通流状态趋于稳定。基于此,分别用线性回归方程、二次方程拟合数据,并且估计得到方程的参数值及检验结果,见表6,结果表明,线性方程与二次方程及参数检验具有统计学意义,相比之下,二次方程更接近实际情况,且经过计算当p=76.8%时得到极小值。

表5 3种情景下对应的λmax值Tab.5 λmaxin 3scenarios

图4 λmax随p的变化趋势Fig.4 Variation tendency ofλmaxchange with p

表6 回归方程参数估计结果及检验Tab.6 Parameters estimation and test for regression models
3 结 论
利用北京市三环快速路实际交通运行数据,借助时间序列非线性特征分析方法,在仿真环境下分析研究了可变限速控制下的局部交通流混沌特征,通过对比相同流量输入前提下有无可变限速策略实施的速度时间序列的λmax,得到如下结论。
1)当没有实施可变限速策略时,所分析的断面位置处的交通流速度时间序列的λmax为正值,存在混沌特征。
2)当实施可变限速策略时,以可变限速下游200m位置为例,仿真情景中的速度时间序列对应的λmax仍为正值,存在混沌特征。
3)在可变限速控制策略下,以可变限速下游200m位置为例,λmax与交通流中依照可变限速值行驶的车辆比例p之间存在二次回归关系,并且当交通流中存在76.8%的车辆按照可变限速值行驶时,交通流存在最小的λmax,且接近于0。
上述结论可从交通流运行特征与车辆速度特征角度为制定合理限速值提供参考,但由于仿真获得的宏观交通流特征是建立在若干假设基础上,与实际存在差异,如流量估计、可变限速值,特别是车辆服从可变限速的情景,在实际交通环境中则较难采集与调查。另外,由于只分析了交通流中依据可变限速值行驶的车辆比例这一因素,其它如驾驶员信息选择与反馈、车辆驶入驶出、具体可变限速值等因素缺少研究,将在后续进一步展开分析。
[1] DISBRO J E,FRAME M.Traffic flow theory and chaotic behavior[M].Washington D.C.:Transportation Research Record,1989:109-115.
[2] DENDRINOS D S.Traffic-flow dynamics:a search for chaos[J].Chaos,Solitons &Fractals,1994,4(4):605-617.
[3] ZHANG X Y,JARRETT D F.Stability analysis of the classical car-following model[J].Transportation Research Part B:Methodological,1997,31(6):441-462.
[4] LI T.Nonlinear dynamics of traffic jams[J].Physica D-Nonlinear Phenomena,2005,207(1):41-51.
[5] SHANG P J,LI X W,KAMAE S.Chaotic analysis of traffic time series[J].Chaos,Solitons &Fractals,2005,25(1):121-128.
[6] NEAAMUDDIN N,JIANG N,MA J M,et al.Active traffic management strategies:implications for freeway operations and traffic safety[C].The 90thAnnual Meeting of Transportation Research Board,Washington,D.C:Transportation Research Board,2011.
[7] HABTEMICHAEL F G,SANTOS L de P.Safety and operational benefits of variable speed limits under different traffic conditions and driver compliance levels[J].Journal of the Transportation Research Board,2013(2386):7-15.
[8] PAPAGEORGIOU M,KOSMATOPOULOS E,PAPAMICHAIL I.Effects of variable speed limits on motorway traffic flow[J].Journal of the Transportation Research Board,2008(2047):37-48.
[9] 卢宇.交通流混沌实时判定方法的研究[D].天津:天津大学,2007.LU Yu.The study on the real-time identification of chaos in traffic flow[D].Tianjin:Tianjin University,2007.(in Chinese)
[10] ROSENSTEIN M T,COLLINS J J,de LUCA C J.A practical method for calculating largest Lya-punov exponents from small data sets[J].Physica D:Nonlinear Phenomena,1993,65(1):117-134.
[11] KIM H S,EYKHOLT R,SALAS J D.Nonlinear dynamics,delay times,and embedding windows[J].Physica D:Nonlinear Phenomena,1999,127(1):48-60.
[12] 范海龙.城市快速路可变限速控制策略研究[D].北京:北京交通大学,2012.FANHailong.Study on variable speed limit control strategy of an urban expressway[D].Beijing:Beijing Jiaotong University,2012.(in Chinese)
[13] ZHAO N L,YU L,ZHAO H,et al.Analysis of traffic flow characteristics on ring road expressways in Beijing[J].Journal of the Transportation Research Board,2009(2124):178-185.
[14] NEZAMUDDIN N,AL-DEEK H.Developing a microscopic toll plaza and toll road corridor model using PARAMICS[J].Journal of the Transportation Research Board,2008(2047):100-110.
[15] LEE C,ABDAL-ATY M.Testing effects of warning messages and variable speed limits on driver behavior using driving simulator[J].Journal of the Transportation Research Board,2008(2069):55-64.
