基于高斯扩散模型的北京市道路交通空气污染的敏感性分析

鲁 楠， 姚恩建， 潘 龙， 潘 征

(1.北京交通大学 城市交通复杂系统理论与技术教育部重点实验室， 北京 100044;2.日电(中国)有限公司， 北京 100084)



基于高斯扩散模型的北京市道路交通空气污染的敏感性分析

鲁 楠1， 姚恩建1， 潘 龙1， 潘 征2

(1.北京交通大学 城市交通复杂系统理论与技术教育部重点实验室， 北京 100044;2.日电(中国)有限公司， 北京 100084)

为准确估算城市道路交通造成的空气污染，通过将高斯扩散模型应用于北京市道路交通空气污染的估算，对模型的适应性和道路交通空气污染对于污染物扩散影响因素的敏感性等进行研究. 首先，在对模型特点分析的基础上，结合研究区域,初步定性地分析模型的适应性；然后，结合北京市空气污染物浓度监测站的实测数据，采用偏差因子等统计指标对高斯扩散模型性能进行评价；最后，基于控制变量方法分析北京市道路交通空气污染对影响扩散的因素(如风速和风向等)的敏感性. 结果显示，高斯扩散模型能较好地适用于北京市道路交通空气污染的估算，而且其对风速、风向和云量有较强的敏感性.

交通工程； 道路交通空气污染； 高斯扩散模型； 敏感性分析

0 引言

随着机动车保有量的快速增长，北京市出现了一系列的交通拥堵和空气污染问题. 经解析论证，其中，PM2.5的来源机动车排放占到31.1%[1]. 因此，治理北京市空气污染的途径之一便是道路交通的控制与管理. 基于此，如何准确地估算预测道路交通造成的空气污染，不仅为环境空气污染质量的预测和人体健康风险评估提供新的思路，更重要的是有利于道路交通管理政策的制定.

针对道路交通空气污染，国外学者较早地开始了研究，提出许多适用于不同场景的模型. 美国斯坦福研究所的Johnson等[2]通过对机动车引起的湍流进行简化假设，提出了适用于两侧有紧密高大建筑物的街道峡谷内的STREET模型；考虑城市道路交叉口处车辆的怠速和加减速，美国环保局开发了仅适用于预测交叉口附近的交通污染物浓度分布的CAL3QHC模型；但上述模型都不适用于开阔道路和城市区域内交通污染物浓度分布的预测，而由Csanady[3]提出且经众多学者改进的高斯扩散模型则得到了广泛的应用. 李东东等[4-6]分别运用高斯扩散模型对济南、厦门、贵州等地的开阔型道路上交通空气污染物扩散分布进行了预测；Hao等[7]基于高斯扩散模型，从交通空气污染角度，对北京市奥运会期间的交通政策的实施效果进行了分析.

高斯扩散模型用简捷的方式最大限度地将空气污染浓度场与气象条件之间的物理联系以及观测事实结合起来，具有较高的时空分辨率和相当的精度；而且高斯扩散模型的数学表达式较为简单，比较容易基于实际分析情景进行修正. 同时，北京市的气象条件(如风速和风向等)较容易获得；北京市路网中有较多较为开阔的道路，如二环和三环等，且拥有35个空气污染监测站，包括5个交通污染控制点，实测数据较多. 因此，高斯扩散模型可能适用于北京市道路交通污染的预测.

为了进一步探究高斯扩散模型对北京市道路交通空气污染预测的适应性，本文拟结合交通数据和气象数据，利用高斯扩散模型对北京市道路交通空气污染物浓度进行预测，并采用偏差因子等统计指标对模型性能进行评价；然后分别针对风向、风速和云量，采用控制变量的方法，比较研究区域中主要快速路附近的污染物浓度在不同气象条件下的区别，从而分析交通空气污染对气象条件的敏感性.

1 研究方法

1.1 研究对象

由于北京市的道路交通主要发生在市区诸如二、三、四环路等城市快速路和主干路，因此，为了研究北京市道路交通空气污染，本文将研究区域限定为五环以内. 如图1所示.

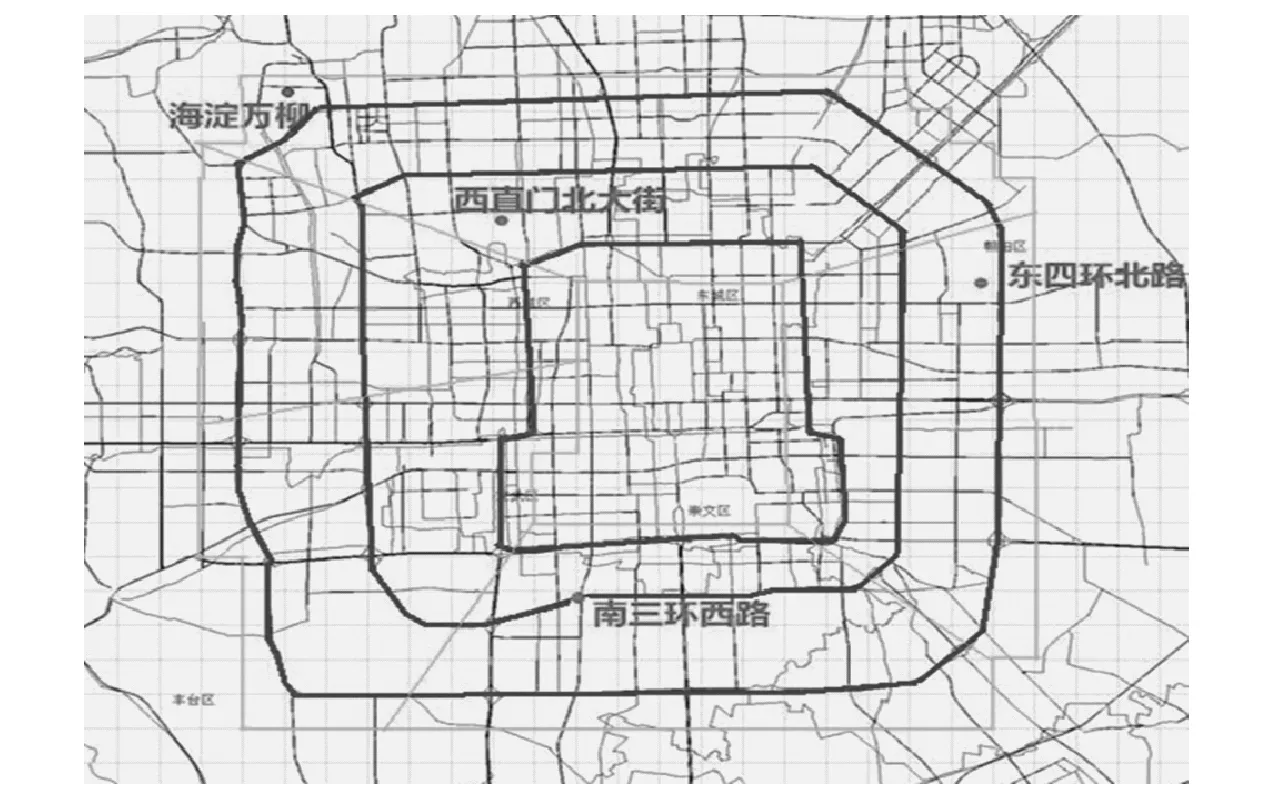
图1 研究区域示意图

该区域内包含二环路约32.7 km，三环路约48.0 km和四环路约65.3 km. 为了计算的方便，用1 km×1 km的网格将该区域进行划分，并以网格的中心点作为污染物扩散的接收点. 每个接收点处的交通空气污染物浓度由所有交通污染源的影响叠加而成；同时，为了简单而有效地评价模型的性能和分析北京市道路交通空气污染对各影响因素的敏感性，本文将部分环境空气监测点(位置如图1)和二、三和四环附近的网格作为载体进行对比分析.

1.2 评价方法

为了验证高斯扩散模型对北京市道路交通污染预测的可靠性，本文将利用在国际空气质量模型验证和协调发展大会上被推荐使用的统计指标，对模型进行评价. 评价指标包括：偏差因子(the Fractional Bias, FB)、归一化均方误差(the Normalized Mean Square Error, NMSE)、几何平均偏差(the Geometric Mean Bias, MG)、几何方差(the Geometric Variance, GV)、皮尔森相关系数R(the Pearson Correlation Coefficient)和FAC2(the Fraction of Predictions within a Factor of Two of Observations)，分别由式(1)～(6)计算：

(1)

(2)

(3)

(4)

(5)

(6)

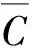
2 结果与讨论

2.1 模型评价

由于交通污染物浓度不可监测，因此本文通过模型预测交通污染物浓度与背景浓度的叠加来估计空气污染物浓度，并与空气污染物监测站的观测值进行对比分析，从而实现交通空气污染扩散模型的评价.

实质上，背景浓度应不包含由交通造成的空气污染，因此我们选择由环保局设定为城市清洁对照点的定陵监测站(位于机动车较少的北京市昌平郊区)的观测值作为背景浓度. 并且，选取定陵监测站(DL)、北京市城市环境评价点之一的海淀万柳(HDWL)监测站和交通污染控制点中的西直门北大街(XZM)和南三环西路(NSH)监测站作为评价参考点. 分别将这些站点于2014年04月01日—10日期间内的CO和PM2.5小时观测值与预测值进行比较并计算评价指标如表1.

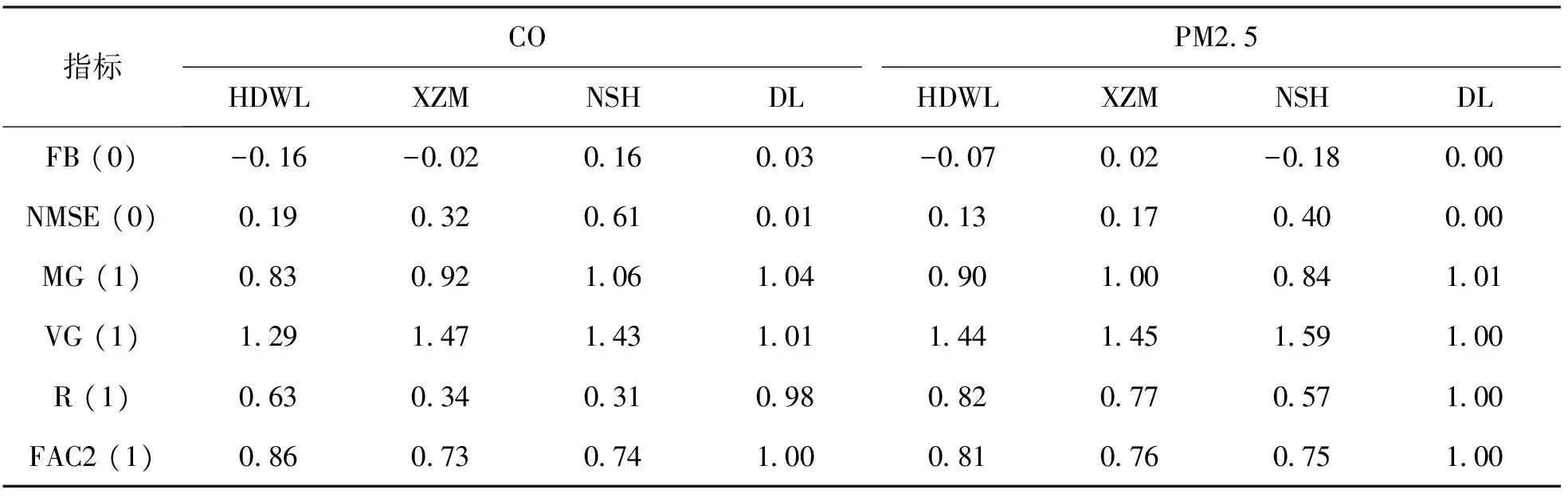
表1 基于各站点的小时平均观测值与预测值的模型评价指标

注：FB(0) 表示指标FB的最佳值为0；其他类似.

总体而言，FAC2介于0.73～1.00，表征模型整体准确性的指标NMSE介于0～0.61，而且考虑系统误差的指标MG介于0.83～1.06，同时考虑系统误差和随机误差的指标VG介于1.00～1.59，模型较好地实现了空气污染物CO和PM2.5的浓度预测. 然而，XZM和NSH站点的CO小时预测值和观测值的相关性不佳，分别为0.34和0.31，但不影响模型整体的准确性.

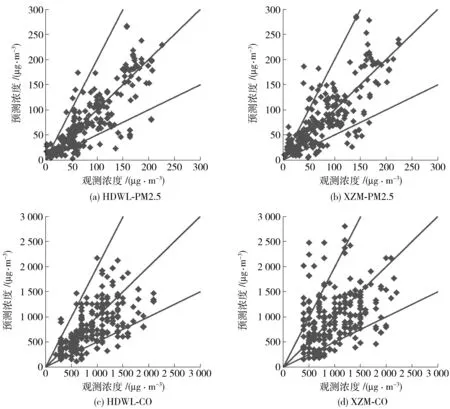
图2 HDWL和XZM站点污染物小时平均浓度散点图

选取HDWL和XZM 2个站点，分别绘制其于2014年04月01日—2014年04月10日内的CO和PM2.5的小时浓度的观测值和预测值的散点图2. 由图可知，HDWL 对于CO的预测有低估的趋势，即使其FAC2较高(FAC2=0.86)；其他较为均匀. 结合表1，对于CO而言，HDWL(FB=-0.16)和XZM(FB=-0.02)的小时平均预测值低于观测值；对于PM2.5而言，HDWL(FB=-0.07)和XZM(FB=0.02)具有相反的趋势.

为了验证模型的预测值是否能符合实际空气污染物浓度在1天内的变化趋势，针对HDWL和XZM 2个站点，分别计算2014年04月01日—2014年04月10日对应时段内的CO和PM2.5的小时平均浓度，并绘制折线图3. 由图可知，空气污染物浓度预测值基本符合实际值在时间序列上的变化趋势，尤其是早高峰较为准确；但是晚高峰有一定的超前性.

综合以上，高斯扩散模型能较好地预测北京市的交通道路空气污染物(如CO和PM2.5)浓度，无论是污染物浓度值还是其随时间的变化趋势.

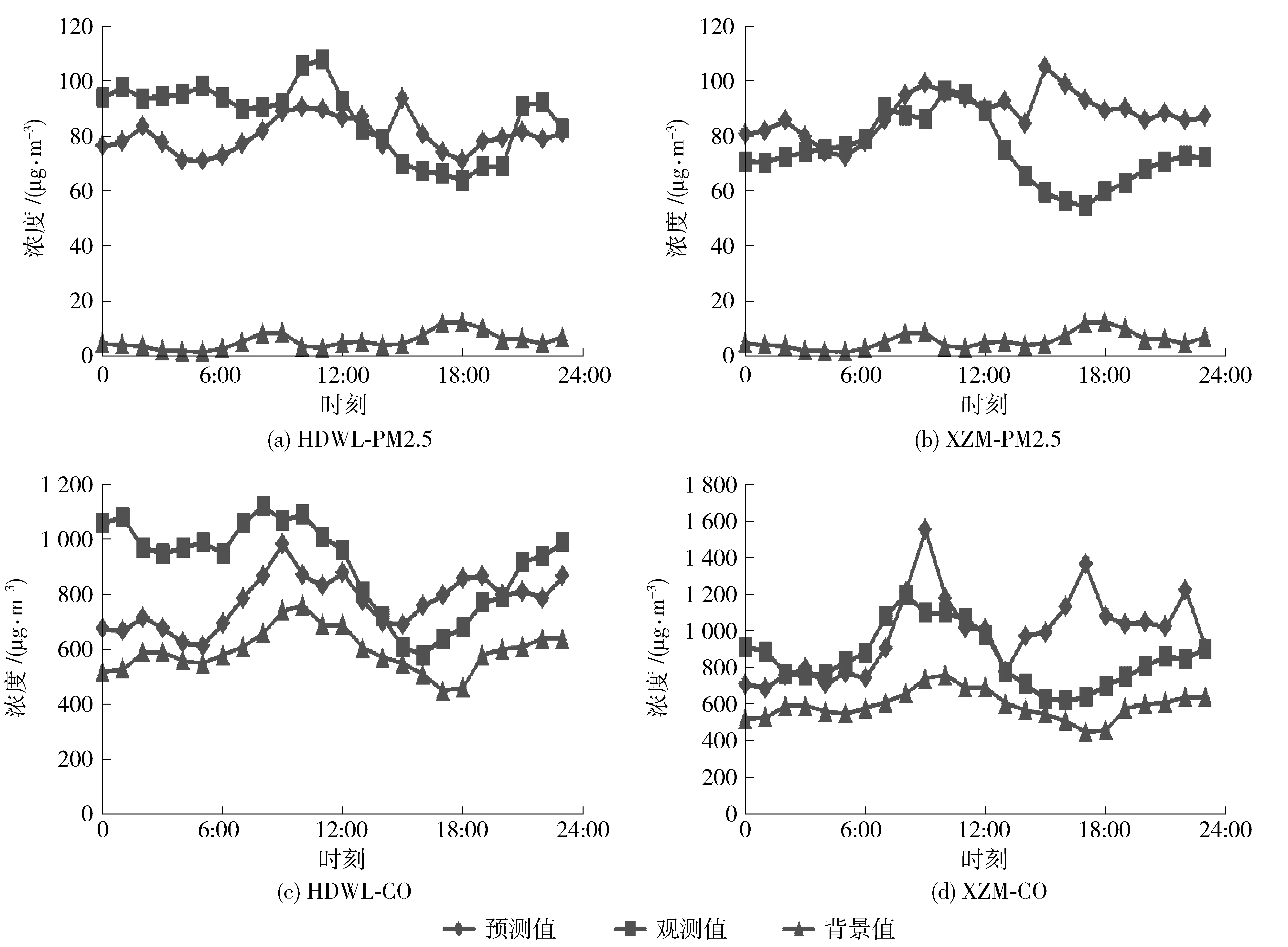
图3 HDWL和XZM站点污染物平均浓度

2.2 敏感性分析

交通空气污染物的扩散过程受到许多因素的影响，如风速、风向和云量等. 而道路交通空气污染分布对这些因素的敏感性程度对预测过程中的数据选取有着很大的影响. 因此，本文将以控制变量的方法，并以北京市二环、三环和四环路上附近的网格中心点处(如图1所示)的污染物浓度为对象来分析北京市道路交通空气污染对这些因素的敏感性.

2.2.1 风速和风向

空气污染物扩散时，风向决定着污染物扩散的方向，且污染物总是分布在污染源的下风向处；风速影响着污染物扩散的速率. 为了探究北京市道路交通空气污染对风速和风向的敏感性，首先，使风向由0°增长到315°，增长幅度为45°，并保持其他变量不变，分别估算HDWL、XZM、NSH和DSH站点处的CO和PM2.5的日平均浓度，其风玫瑰图如图4；然后，使风力由1级增长到3级，即风速为0.9、2.5、4.3 m/s，并保持其他变量不变，估算二、三和四环路附近的接收点处的CO一天内各小时平均浓度，如图5.

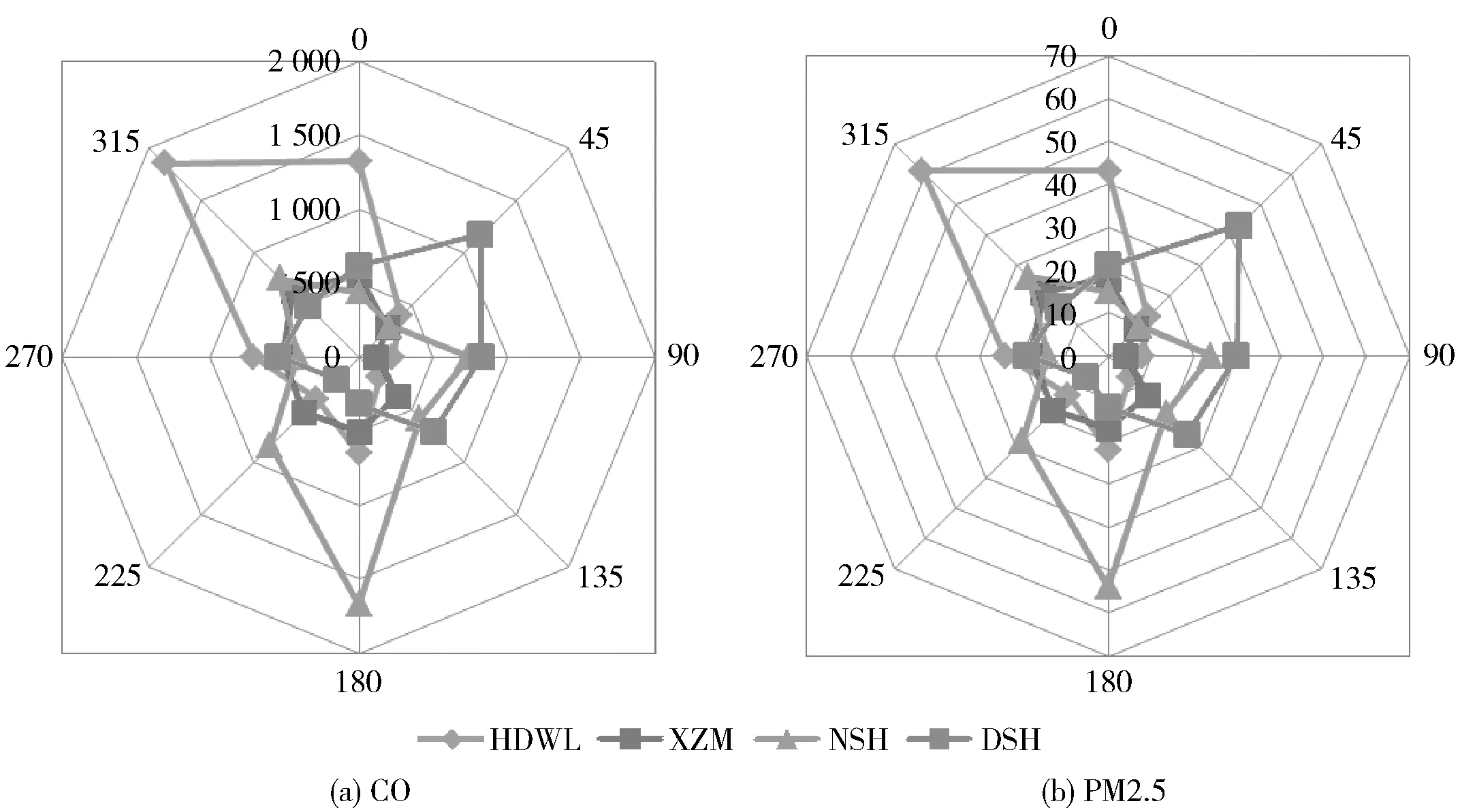
图4 不同风向下4个监测站处CO和PM2.5日平均浓度

图5 各风力等级下二、三和四环路附近接收点处CO小时平均浓度

由图4可知，随着风向的变化，各站点的CO和PM2.5浓度呈现相同的变化趋势. 而且，当污染物接收点位于风向下方时，其污染最严重；反之，污染浓度最小. 如位于研究区域西北处的HDWL站点，当风向为315°(西北风)时，污染物浓度最大(CO日平均浓度为1 847 μg/m3，PM2.5为61 μg/m3)；相反，当风向为135°(东南风)时，污染物浓度最小(CO日平均浓度为193 μg/m3，PM2.5为7 μg/m3)，两者相差约9倍.

图5显示，当其他变量不变的情况下，一级风力(风速为0.9 m/s)时，交通空气污染物CO的小时平均浓度最低；相反，二级风力(风速为2.5 m/s)时，CO的污染最严重. 二级风力时的CO日平均浓度约为三级时的1.4倍，三级风力时约为一级时的1.7倍. 其原因在于风速较大时，空气污染物的扩散速度虽然较快，但对于接收点而言，对其造成影响的污染源增加；相反，风速较小时，空气污染物的扩散速度虽然较慢，但对接收点造成影响的污染源减少.

2.2.2 云量

云量对空气污染物扩散的影响主要通过影响大气稳定度间接地影响污染物扩散的速度，不同的风速下，其影响程度不同，本文分别在不同风力等级下，使云量由0.1增加到0.9，增长幅度为0.2，采用高斯扩散模型估算北京市道路空气污染物CO的浓度，并计算二、三和四环附近接收点处CO日平均浓度，如图6. 在风力为1级和2级的情况下，CO日平均浓度随云量呈线性变化的趋势，且云量每增加0.1，CO日平均浓度分别增加约500 μg/m3和200 μg/m3；而风力为3级的情况下，当云量小于0.5时，CO的日平均浓度随云量的变化也具有线性趋势，但当云量大于0.5时，CO日平均浓度随云量的增加而先增大后减小，并在云量为0.7时达到最大.

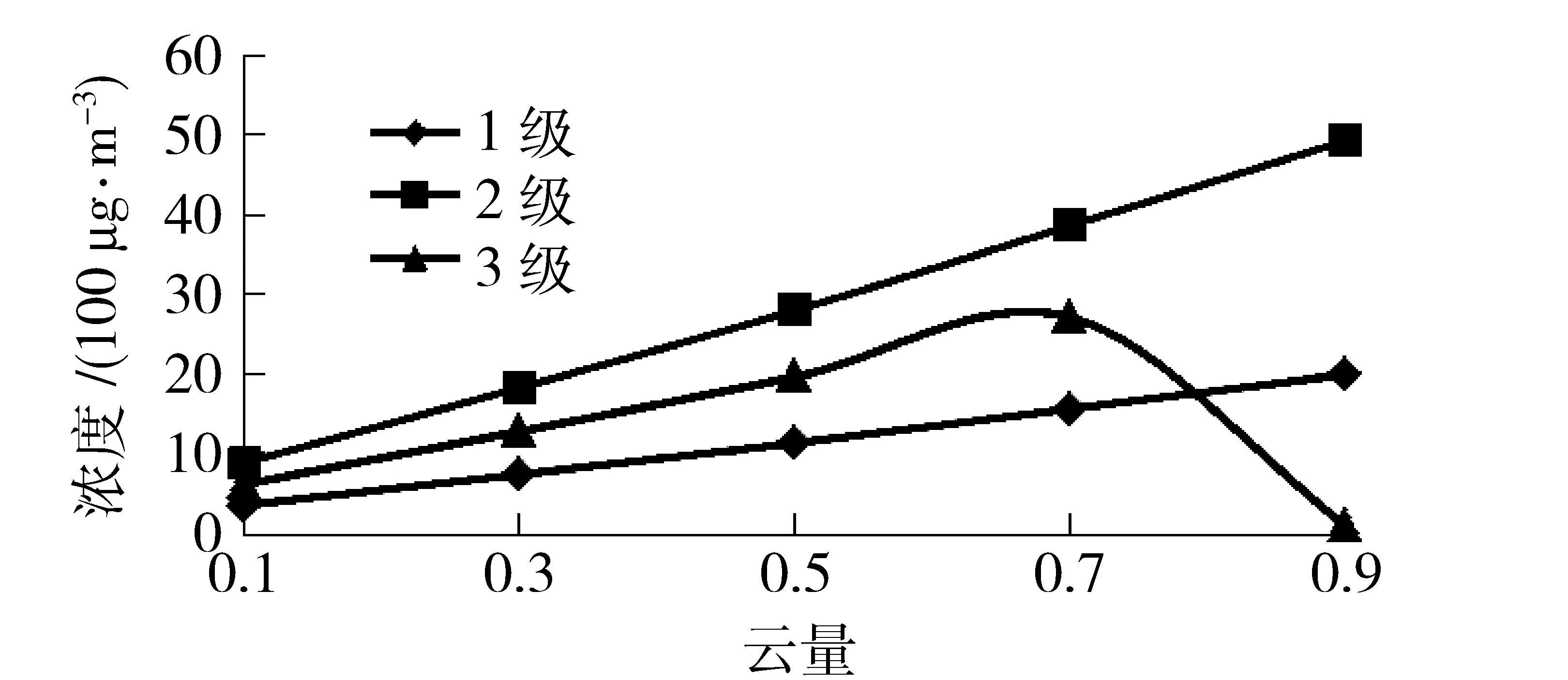
图6 各级风力下二、三和四环路附近接收点处CO日平均浓度随云量变化图

3 结论

本文通过北京市4个空气监测站位置的空气污染物浓度的平均小时预测值与实测值的对比，对基于高斯扩散模型的北京市道路交通空气污染估算的效果进行了评价；采用控制变量方法分别分析了其对于风速、风向和云量变化的敏感性. 结果显示，表征模型整体准确性的指标NMSE介于0～0.40，考虑系统误差的指标MG介于0.83～1.06，同时考虑系统误差和随机误差的指标VG介于1.00～1.59，表明高斯扩散模型能有效地估算北京市道路交通空

气污染(CO和PM2.5)；而且，北京市道路交通空气污染对风速、风向和云量等因素有较强的敏感性. 因此，采用高斯扩散模型进行北京市道路交通空气污染的预测时，应加强上述影响因素数据采集的精度要求，以使预测结果更加精确.

[1] 侯景新. 治理北京空气污染正当时[J]. 前线, 2014(5): 76-78.

[2] Johnson W B, Ludwig F L, Dabberdt W F, et al. An urban diffusion simulation model for carbon monoxide [J]. Journal of the Air Pollution Control Association, 1973, 23(6): 490-498.

[3] Benson P E. A review of the development and application of the CALINE3 and 4 models[J]. Atmos Environ B Urban Atmos, 1992, 26(3): 379-390.

[4] 李东东, 刘厚凤, 杜瑞雪. 应用CALINE4模式估算机动车排放污染物的浓度——以济南市主干道为例[J]. 资源开发与市场, 2009, 25(1) : 53-54.

[5] 陈红梅, 陈崇成, 汪小钦. 应用CALINE4模式模拟机动车排气污染的时空分布——以厦门市主干道路为例[J]. 福州大学学报: 自然科学版, 2004(4): 257-260.

[6] 付甫刚, 马旭东, 周晓娟. CALINE4模式在贵州省安顺至紫云高速公路机动车尾气污染环境影响评价中的应用[J]. 三峡环境与生态, 2011, 33(2): 53-57.

[7] Cai Hao, Xie Shaodong. Traffic-related air pollution modeling during the 2008 Beijing Olympic Games: The effects of an odd-even day traffic restriction scheme [J]. Science of the Total Environment, 2011, 409: 1935-1948.

Sensitivity Analyses of the Traffic-related Air Pollution in Beijing Based on Gaussian Dispersion Models

LU Nan1, YAO En-jian1, PAN Long1, PAN Zheng2

(1.MOE Key Laboratory for Urban Transportation Complex Systems Theory and Technology, Beijing Jiaotong University, Beijing 100044, China; 2.NEC Labs China, NEC Co., Ltd., Beijing 100084, China)

Accurate estimation of the traffic-related air pollution. This study aims to apply the Gaussian dispersion models to the estimation of traffic-related air pollution in Beijing, evaluate the models performance and analyze the sensitivity of the traffic-related air pollution to factors of pollutants dispersion. Firstly, based on the analysis of model features, adaptability of the model was qualitatively analyzed combined with the study domain; secondly, the evaluation of the model performance was carried out by comparing the observed hourly concentrations of CO, PM2.5 at several monitoring sites in Beijing with model predictions, using a widely used statistical framework for model evaluation; then, the sensitivity of traffic-related air pollution in Beijing to factors influencing the dispersion (such as wind speed and direction, etc.) was analyzed with the control variable method. Results showed the model predictions of traffic-related air pollution in Beijing turned out reasonably satisfactory, and the factors make a great influence on the forecast.

traffic engineering; traffic-related air pollution; Gaussian dispersion models; sensitivity analyses

10.13986/j.cnki.jote.2015.02.011

2014- 10- 11.

国家973项目(2012CB725403)；高等学校博士学科点专项科研基金(20130009110002).

鲁 楠(1990—)，男，硕士研究生，研究方向为交通运输规划与管理. E-mail：13120878@bjtu.edu.cn.

U 491.9+2

A

1008-2522(2015)02-55-06