带干扰的农民工医疗保险风险模型①

杨 璐，陈奕含，王志福

(渤海大学 数理学院，辽宁 锦州121001)

0 引 言

农民工是个特殊的群体，面临着健康和医疗无保障双重困境.目前，有人提出购买医疗保险的观点，在此基础上，本文研究了文献［1－2］并联系实际，建立了保费收入和理赔为复合Poisson 过程的带干扰的风险模型［3］，同时考虑了随机利率，最终得到调节系数，破产概率表达式，通过某市八个行业的数据分析，估算出保险公司的破产概率与初始资本的关系.

1 模型的建立

其中U(t)为保险公司t 时刻的盈余，u=U(0)(u＞0)为时刻0 的初始资本;I 为随机利率.对于模型(1)，作如下假设:

(1)Xj为保险公司第j 张保单收取的保费，Yj为保险公司第j 次的理赔额，且{Xj，j=1，2，…}与{Yj，j=1，2，…}为恒正的独立同分布的随机序列，其分布函数分别为F(x)，G(y)，E(Xj)=μ1，

(2)M(t)，N(t)分别为保险公司截止时刻t 的保单数和理赔次数;且{M(t)，t ≥0}，{N(t)，t ≥0}是参数分别为λ1，λ2的Poisson 过程，M(0)=0，n(0)=0;

(3){W(t)，t ≥1}为标准的布朗运动，表示保险公司的不确定收入与支出，b 为干扰因子;

(4)S(t)为到t 时刻的理赔额［4］;

(5){Xj，j = 1，2，…}，{Yj，j = 1，2，…}，{M(t)，t ≥0}，{N(t)，t ≥0}相互独立;

若不考虑初始资本，模型(1)可写为

即在某时刻t 时保险公司的盈余过程，其中如果保险公司的盈余小于零，可视之为破产.

定义1: 破产时刻:T=inf{t:U(t)＜0}，最终破产概率Ψ(u)=P{T ＜∞|U(0)=u}，相对安全系数;当θ=0 或θ ＜0 时破产.

2 医疗保险模型的破产概率

引理1 对于盈余过程［5］，{G(t)，t ≥0}，存在函数使得E［e－rG(t)］=exp(tg(r)).

引理2 对于g(r)，则方程g(r)=0 在r ＞0内有唯一正解R，称R 为调节系数.

证明: 由于

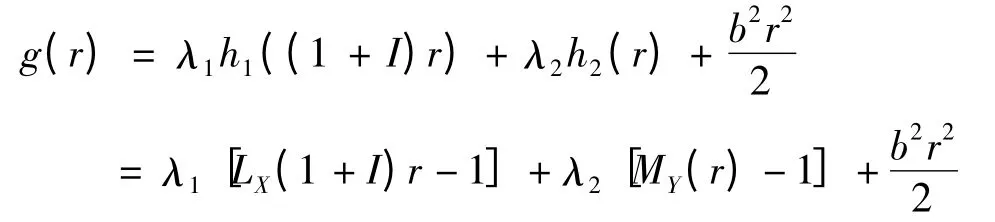
故

又易知

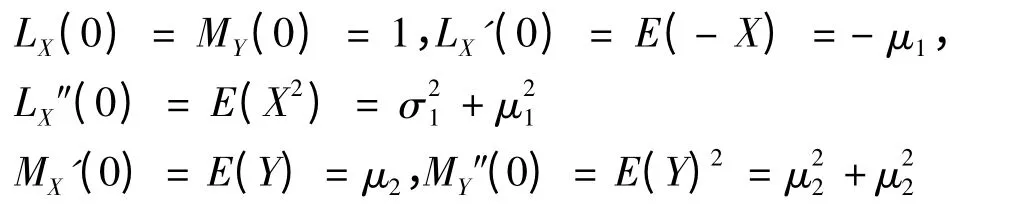
所以

从而g(r)是具有极小值点的下凸函数，

则g(r)在r ＞0 内有唯一极小值点

故方程g(r)=0 有唯一正解，设该解为R，R即为调节系数.

证明:

当r 取调节系数R 时，有E［e－RU(t)］=e－Ru(1+I)，则上式可化为

由

当t →∞时，

以下证明limt E［e－RU(t)|T ＞t］P(T ＞t)=0 E［U(t)］=u(1+I)+λ1tμ1－λ2tμ2=u(1+I)+ωt

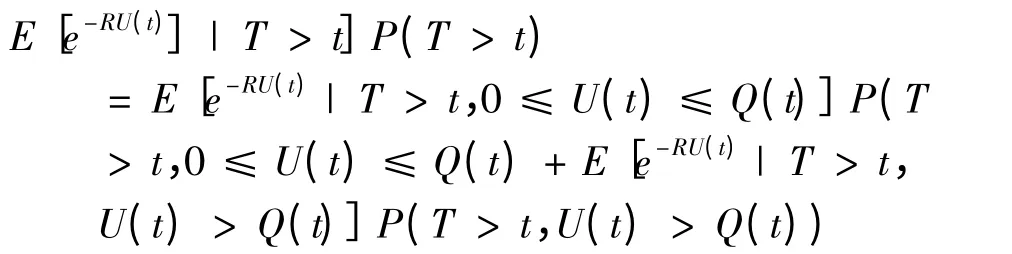
由切比雪夫不等式，

当t →∞时，

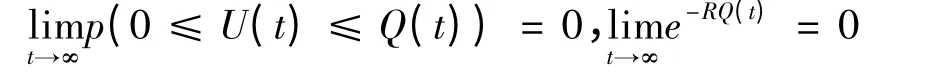
所以

从而得到，

由在t ＜∞上，－RU(T)≥0，可知E［e－RU(T)|T ＜∞］≥1

由此可得

3 医疗保险模型的应用

3.1 医疗保险购买情况调查

为得到模型(1)中Poisson 过程中参数值，通过对J 城市部分主要行业中农民工是否有意向购买医疗保险进行调查统计，得到部分农民工购买意愿的统计结果如下:

表1 农民工购买医疗保险意愿问卷数据分析

根据表中统计数据，可以通过购买者比例来估算各行业中医疗保险的购买人数.假设城市八个主要行业每个行业从业人员大约有2000 人，则通过上表相应比例可得各行业有购买医疗保险意向人数分别为:417 人，546 人，576 人，758 人，650 人，599 人，671 人，733 人.

做无偏估计得:

3.2 医疗保险破产概率Ψ(u)的估算

通过对保险公司的保单和理赔数据进行分析我们可以得到，每笔保单的Xj服从指数分布，参数大约为α=1，每笔理赔额Yj也服从指数分布，参数大约为

在模型(1)中I 为一年的年利率，设I =3.3%，农民工患病率0.18，则λ2=0.18.干扰因子b=0.2，由以上计算可知:

令g(r)=0 得R ≈3.43×10－4

当u=10000 时，将R=3.43×10－4，i=3.3%代入(3)式得Ψ(u)≤2.89%;

当u=20000，30000，50000 时，可以计算出破产概率的上界，如表2:

表2 破产概率的上界

由上表可知，主要影响破产概率的因素为初始资本，初始资本越多，破产概率越低，这与保险公司的实际运营是一致的.当然本文也存在一些误差，如样本较小，对一些变量的取值较小等［6］，这些结果都会影响实际运营.伴随市场经济的日益复杂，继续深入和完善风险理论是非常有价值的，该课题的研究也一定会有更广阔的前景.

［1］ 边宽江，张振力，蒋红敬.金融危机下的农民工失业保险模型探究［J］.安徽农业科学，2010，11:5946－5947.

［2］ 陈汉平，何谦.农民工失业保险研究述评［J］.当代经理人，2008，(21):1292－1293.

［3］ 陈松男.金融工程数学［M］.上海:复旦大学出版社，2002:1－15.

［4］ 解俊山.保险风险模型破产理论的若干成果［J］.西北工业大学，2006.

［5］ 黎锁平，刘琪.考虑投资和干扰具有随机保费的离散风险模型［J］.高校应用数学学报，24(1):9－14.

［6］ AsmussenS.Ruin Probailities［M］，World Scientific，2000.

［7］ 张振力.利率环境下几类金融风险模型的破产问题研究［D］.杨凌:西北农林科技大学，2010－05－01.

［8］ 黄雯婷.关于两种推广风险模型的研究［D］.重庆:重庆大学，2009－04－01.