一类含混合时滞非自治神经网络的指数稳定性①

徐至晨，陈爱珍，周宗福

(安徽大学 数学科学学院，安徽 合肥230601)

故系统(1)是α－指数稳定的.定理2 证毕.

0 引 言

在过去的几十年里，已经注意到非自治神经网络已经在越来越多的领域得到应用，如影像信号传输、图像识别等.关于非自治神经网络系统的研究成果也层出不穷(见文献［1 ～4］).文献［4］讨论了一类混合时滞非自治神经网络系统的指数稳定性，利用Lyapunov－Krasovskii 泛函和黎卡提方程等分析方法，给出了这类系统的指数稳定性的充分条件.在文献［4］所研究的系统中，引入了新的控制函数，研究了更为一般的含混合时滞的非自治神经网络系统，获得这一新系统的指数稳定性的若干结论.

本文讨论如下非自治神经网络系统:

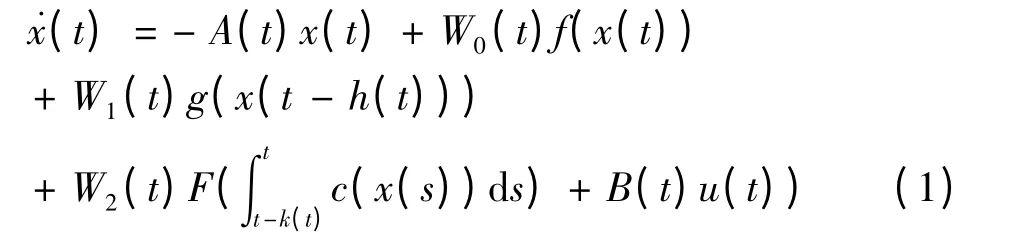
其中x(t)∈Rn，A(t)∈Rn×n，W0(t)，W1(t)，W2(t)∈Rn×n，这里B(t)∈Rn×m为控制输入矩阵，f，g，c，F:Rn→Rn，且

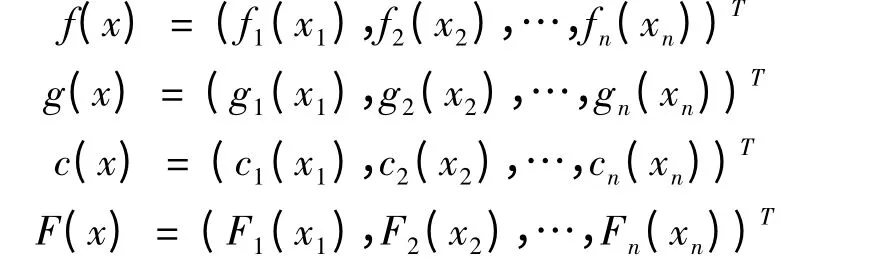
假设:(D1)0 ≤h(t)≤h0，˙h(t)≤u(u ＜1)，0 ≤k(t)≤k0，∀t ≥0;(D2)0 ≤h(t)≤h0，0 ≤k(t)≤k0，∀t ≥0

在系统(1)中，初始函数φ(t)∈C(［－d，0］，Rn)，其中，d=max{h0，hk}.

1 有关定义及引理

假定:

(H1)矩阵函数A(t)，W0(t)，W1(t)，W2(t)，B(t)在［0，+∞)上是连续的;

(H2)存在非负常数ai，bi，ci，di(i =1，2，3，…，n)，使得:

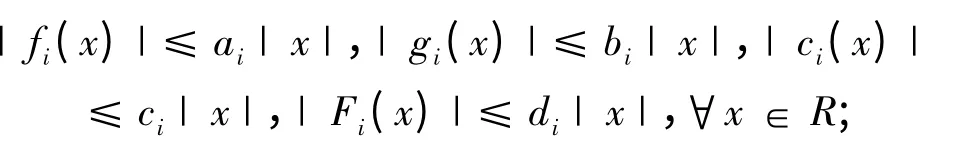
(H3)令Y(t)=A(t)+AT(t)+λB(t)BT(t)，，使得，其中，λmin(Y(t))表示Y(t)的最小特征值.

定义1 设α ＞0，称系统(1)是α－指数稳定的，如果存在一个状态反馈控制函数u(t)使得系统(1)的 解 x(t，φ)满 足 ‖x(t，φ)‖ ≤β‖φ‖e－αt，(t ≥0)，其中β ＞0 为常数.

引理1 (Cauchy 矩阵不等式)对于x，y ∈Rn及正定阵N ∈Rn×n，有

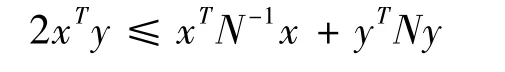
引理2 (Jesen－based interal 不等式)对于任一给定的正定阵M，v ∈R，且v ＞0，向量函数w:［0，v］→Rn，有下列不等式成立:

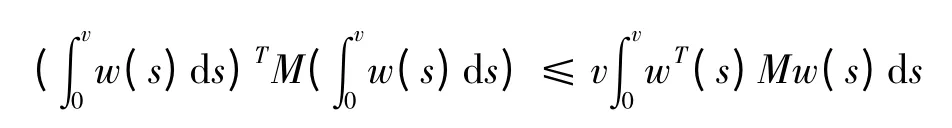
2 主要结果

引入下列符号:

对于α ＞0，P(t)为［0，+∞)上的半正定矩阵，令:

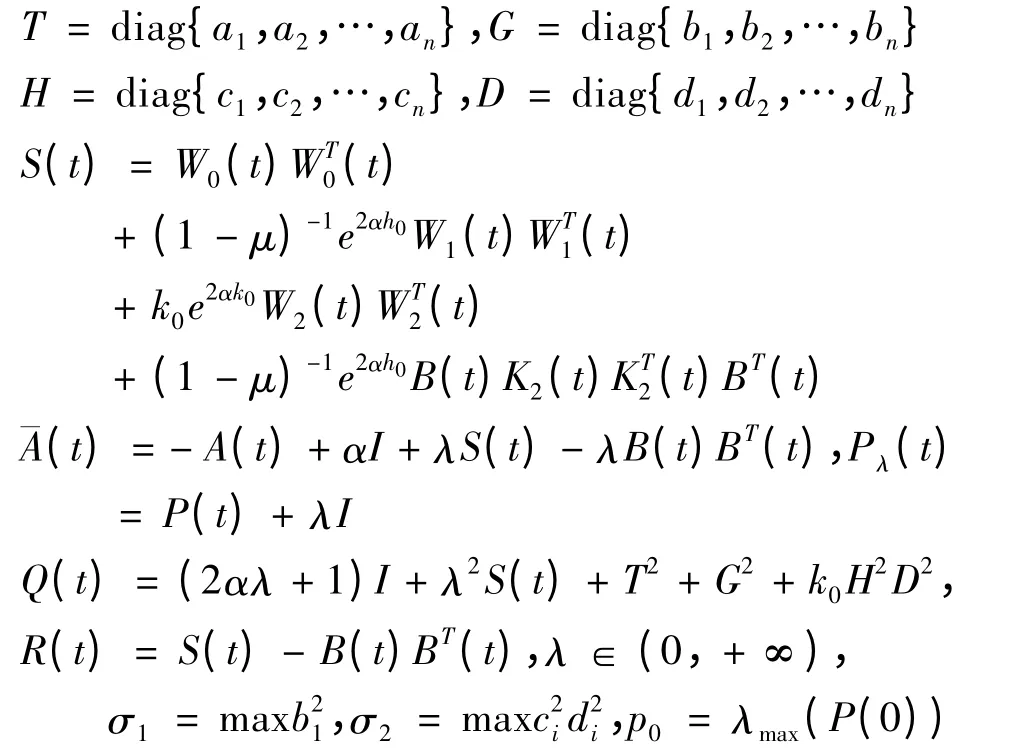
定理1 假设(H1)～(H3)，(D1)成立且存在α ＞0 及半正定阵P(t)，满足黎卡提方程

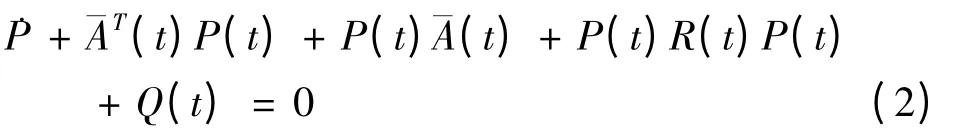
且设:u(t)=K1(t)x(t)+K2(t)x(t－h(t))，其中连续，则系统(1)是α－指数稳定的.

证明: 作Lyapunov 泛函

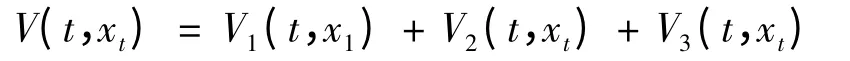
其中，

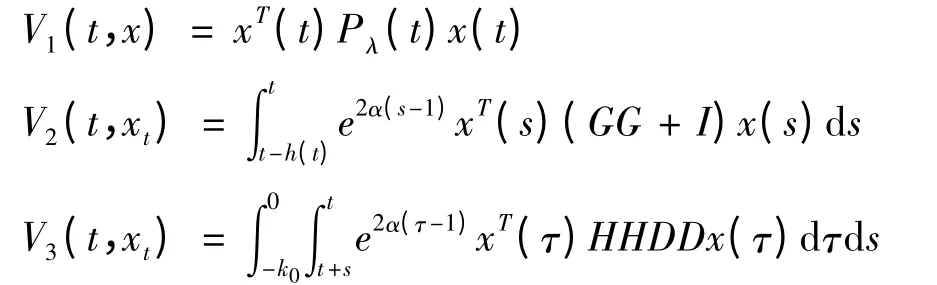
易知:

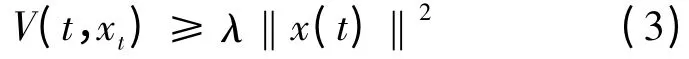
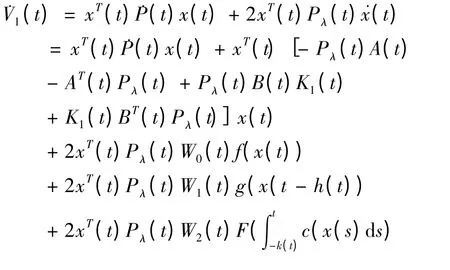
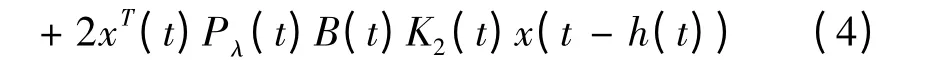
由引理1 和引理2 可以得到:

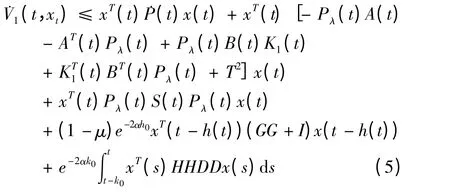
同样地，对V2(t，xt)，V3(t，xt)关于t 求导得到:

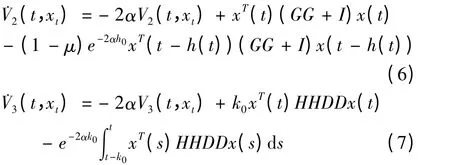
由(5)～(7)得到:

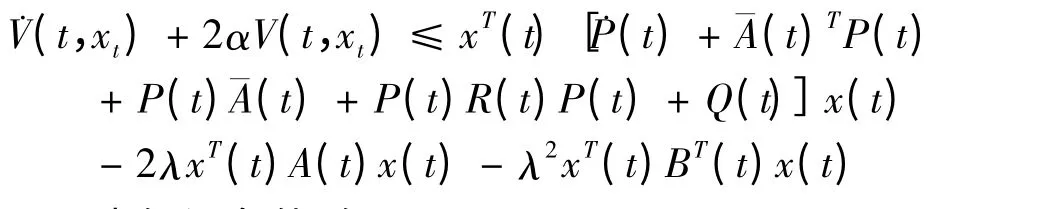
由假设条件，得:

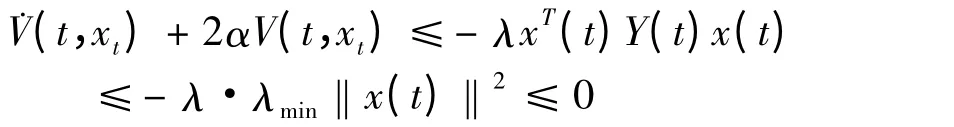
从而，V(t，xt)≤V(0，x0)e－2αt，∀t ≥0，又由于:

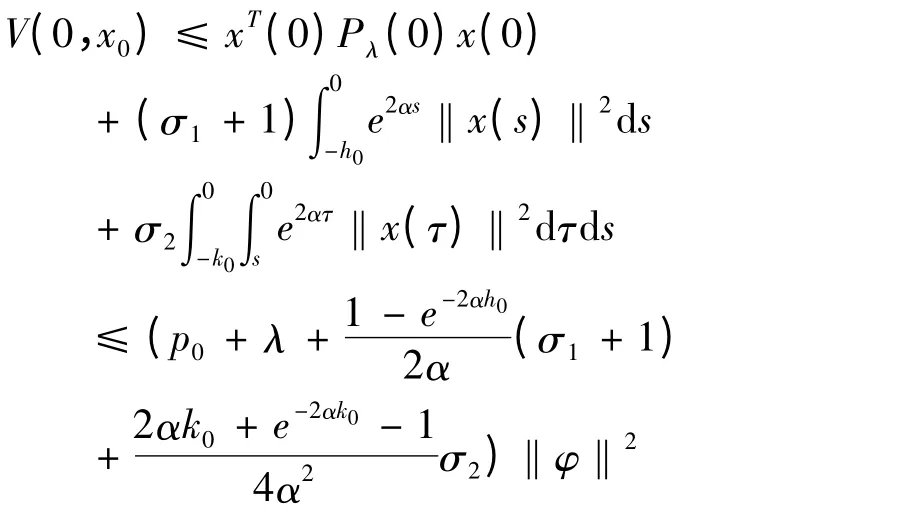
结合(3)即得:‖x(t，φ)‖≤β‖φ‖e－αt，∀t≥0，其中，

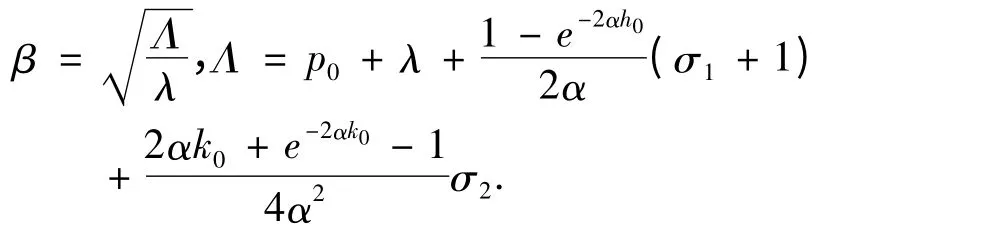
所以，系统(1)是α－指数稳定的.定理1 证毕.

设P(t)为有界半正定矩阵，λ ＞0，ε ＞0 引入记号:

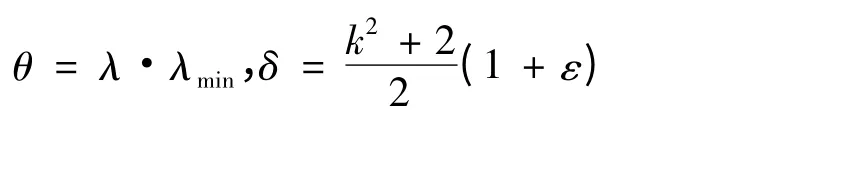
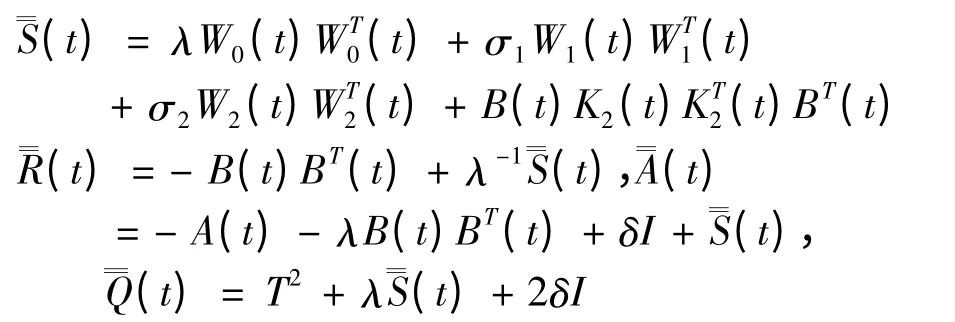
定理2 在(H1)～(H3)以及(D2)成立的条件下，若存在一个半正定的有界矩阵P(t)，满足黎卡提方程:

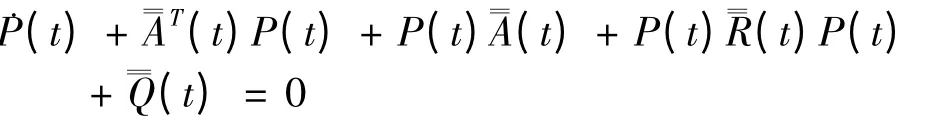
且设

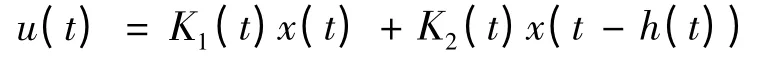
证明: 构造V 函数如下:

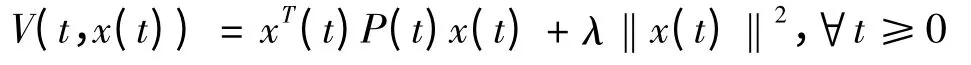
则

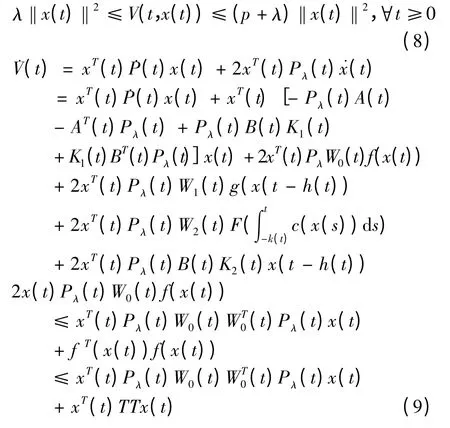
由泛函微分方程的Razumihkin 定理的假设条件，并利用引理1 和引理2 可得:

当V(t+s，x(t+s))＜qV(t，x(t))，q ＞1，∀s∈［－d，0］，q=1+ε，t ＞0 时，

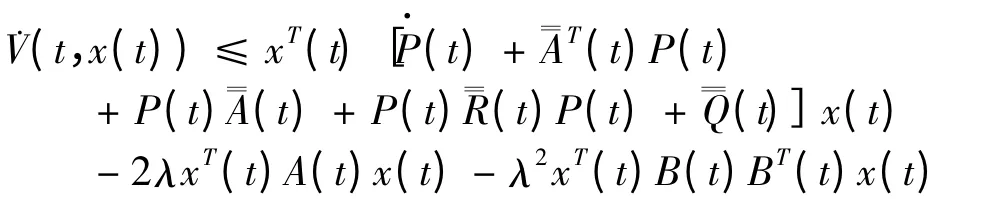
即有

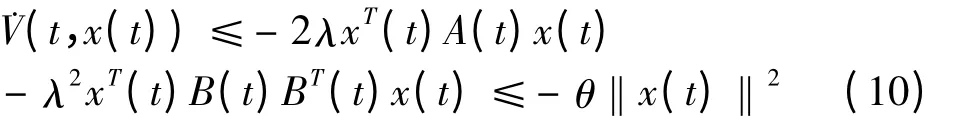
由Razumihkin 定理可知系统(1)的零解是一致渐近稳定的.

再由(8)和(10)可知:

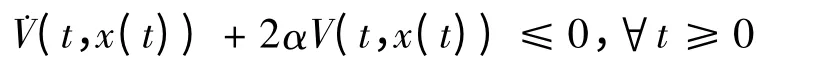
故

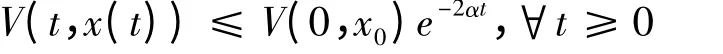
综合前面可得:

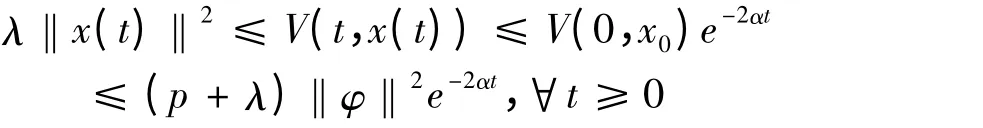
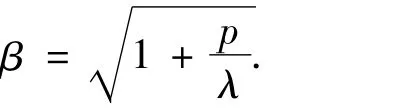
故系统(1)是α－指数稳定的.定理2 证毕.

［1］ L.O.Chua，L.Yang.Cellular Neuralnet Works:theory［J］.IEEE Trans.Circ.Syst，1998，10:1257－1272.

［2］ W.Chen，Q.Ma，G.Miao et al.Stability Analysis of Stochastic Neural Networks with Markovian Jump Parameters Using Delay－Partitioning Approach［J］.Neurocomputing，2013，103:22－28.

［3］ X.Lou，B.Cui，On Robust Stabilization of a Class of Neural Networks with Time－Varying Delays［J］.Proc.IEEE Int.Conf.Comput.Intel.Security，2006:437－440.

［4］ M.V.Thuan et al.Exponential Stabilization of Non－Autonomous Delayed Neural Networks Via Raccati Equations［J］.Applied Mathematics and Computation，2014，246:533－545.