爆轰波波形与药型罩结构匹配对杆式射流成形的影响*
2015-04-12王晓鸣李文彬李伟兵董晓亮
陈 闯,王晓鸣,李文彬,李伟兵,董晓亮
(南京理工大学智能弹药技术国防重点学科实验室,江苏 南京 210094)
爆轰波波形与药型罩结构匹配对杆式射流成形的影响*
陈 闯,王晓鸣,李文彬,李伟兵,董晓亮
(南京理工大学智能弹药技术国防重点学科实验室,江苏 南京 210094)
为提高杆式射流对钢靶的侵彻能力,设计了一种偏心亚半球药型罩,通过爆轰波碰撞理论推导出药型罩压垮速度,并结合改进的PER理论建立了杆式射流成形的模型。分析了药型罩结构参数对爆轰波碰撞压力的影响规律,获得了等质量变壁厚药型罩射流质量及速度分布的变化规律。结果表明:马赫反射压力随偏心距的增大而增大,随外壁曲率半径的增大而减小,而正规斜反射压力与马赫反射压力变化规律相反,且马赫反射压力受药型罩结构影响较大;通过对比不同方案,罩顶与罩口部厚、中间薄形状药型罩形成的射流质量提高了29.5%,头部速度提高了21.3%,且速度梯度最大,相同炸高条件下侵彻深度提高了约2倍装药直径。针对优化结构进行了数值模拟和实验验证,通过对爆轰波波形与药型罩结构合理的匹配设计,使形成的杆式射流成形及侵彻性能得到显著提升。
爆炸力学;杆式射流;侵彻;爆轰波波形;偏心亚半球药型罩
杆式射流是一种介于射流和爆炸成形弹丸之间的聚能侵彻体,具有射流速度高、质量大、杵体小、侵彻能力强、孔径均匀等优点[1]。既可以用于串联战斗部的前级装药为后级开辟侵彻通道,又可以攻击间隔装甲、反应装甲、水介质以及混凝土等多种目标,杆式射流成形机理成为成形装药领域研究的热点问题之一[2-3]。
A.Blache等[4]通过调节VESF板形状等方法获得期望的爆轰波形,利用辅助装药驱动VESF板起爆主装药得到高速杆式射流,并实验验证了其具有很好的大炸高性能。R.J.Funston[5]设计了一种多功能起爆装置,通过改变起爆方式实现成形装药战斗部的多功能性,环形起爆时产生高速杆式射流。黄正祥等[6]通过理论分析研究了起爆方式对聚能杆式侵彻体成形参数的影响,并通过实验进行了验证。吴晗玲等[7]利用数值模拟与实验的方法研究了平面截顶型和球缺型结构药型罩压垮过程,得到了杆式射流形成、延伸和失稳断裂的全过程。但是以上研究没有考虑爆轰波波形与药型罩结构之间的匹配对杆式射流成形的影响,有必要以增大射流质量和速度梯度为目标对成形装药结构进行优化设计,以提高成形装药的侵彻威力。
本文中利用爆轰波碰撞产生的马赫反射压力和正规斜反射压力求解作用于药型罩的压垮速度,并将其引入改进的PER理论建立杆式射流成形的模型。分析偏心亚半球药型罩结构参数对爆轰波碰撞压力的影响规律,通过改变壁厚优化设计装药结构,获得提高射流质量、增大射流速度的方法,并进行侵彻实验验证。
1 杆式射流成形的理论模型
1.1 装药结构
成形装药结构如图1所示,装药直径110 mm、高125 mm,其中辅助药柱的厚度为5 mm。隔板直径Dg=100 mm,半锥角m=54°,张角n=5°,隔板采用酚醛树脂。壳体材料选择钢,厚度为6 mm,壳体上方设计成敞口形状便于放入传爆装置,起爆点为O点。药型罩采用偏心亚半球罩[8],其结构由外壁曲率半径rL、偏心距a和壁厚h等参数控制。
1.2 爆轰波传播过程分析
杆式射流的成形过程是通过隔板控制爆轰波在炸药中的传播形状,从而改变爆轰波对药型罩的入射角、增大压垮速度、提高射流质量。装药起爆后,爆轰波绕过隔板向药型罩传播,在此过程中爆轰波将在轴线处发生碰撞,根据碰撞时爆轰波之间夹角的不同可以分为正规斜碰撞和马赫碰撞,爆轰波传播过程如图2所示。
当装药在点O起爆后,爆轰波绕过隔板到达O1,这时可以看作以O1为圆心形成环形起爆爆轰波在炸药中传播,爆轰波最先在轴线上点G发生碰撞,入射角为爆轰波阵面与轴线的夹角ΨG,碰撞点沿轴线从点G移动到点A的过程中入射角逐渐增大,F.Muller[9]通过实验发现当入射角增大到约44.5°时反射波将与固壁脱离,在固壁附近形成马赫波。图2中点A的入射角Ψm=44.5°,入射角达到临界值,点A即为正规斜碰撞与马赫碰撞的分界点。
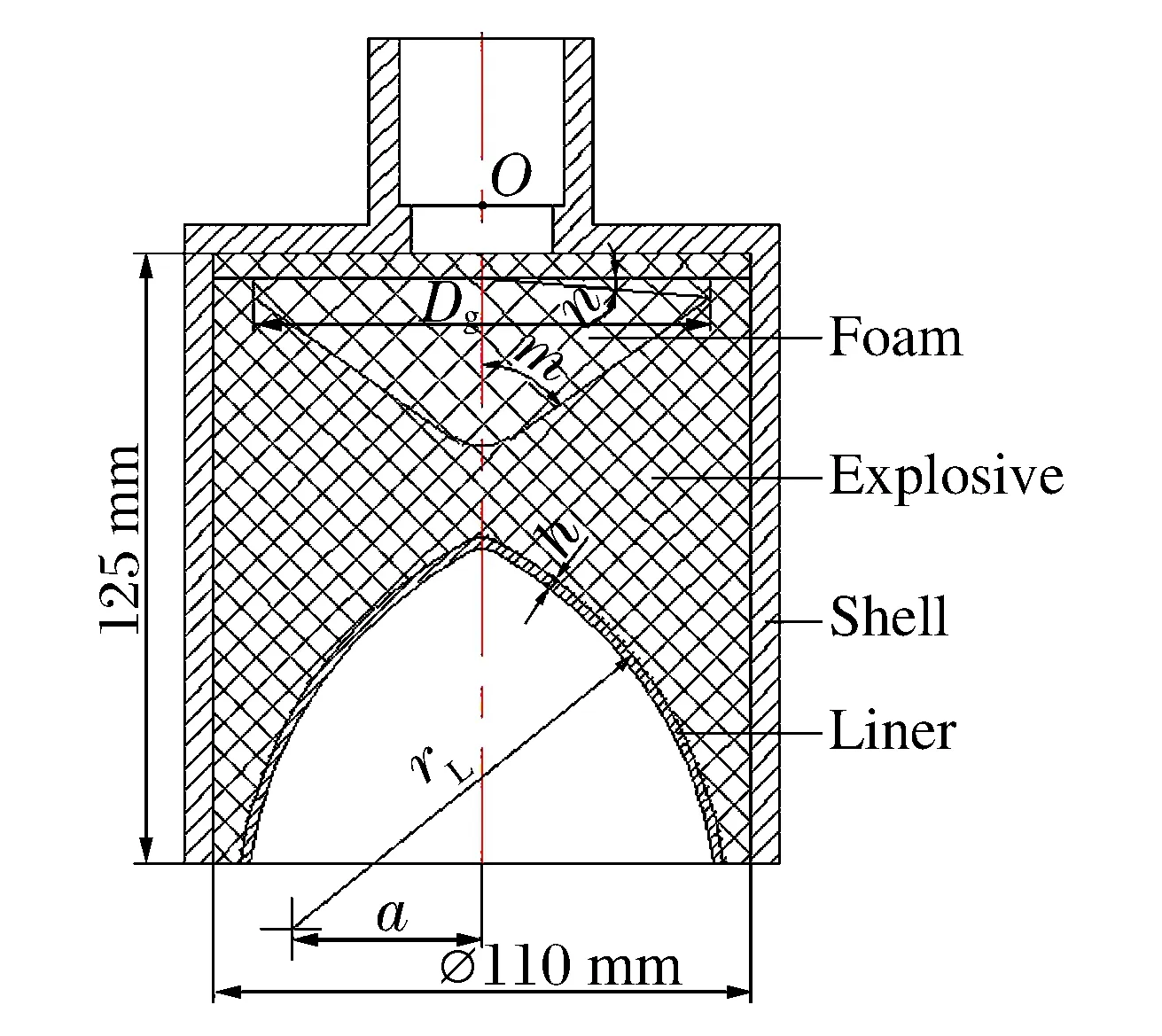
图1 成形装药结构Fig.1 Configuration of shaped charge

图2 爆轰波传播过程Fig.2 Propagation process of detonation wave
发生马赫反射后,反射波逐渐脱离装药轴线,图中AC代表马赫杆的移动方向,三波点C为爆轰波传到点C时入射波波阵面CE、反射波波阵面CD和马赫杆CB的交点,三波点附近流场被CA、CB、CD、CE分为4个区域。马赫杆运动方向与轴线的夹角为α,从图2中可以看出三波点处入射角Ψ0为入射波阵面CE和轴线夹角与α的差,α可以根据下式得到[10]:
(1)
式中:u0=Dc/sinΨ0,其中Dc为炸药的爆速;p1、p4分别为Ⅰ区和Ⅳ区的压力;ρ1、ρ4分别为Ⅰ区和Ⅳ区的密度:
(2)
式中:pCJ为炸药CJ压力,η为过度压缩系数,取η=1.1。马赫杆传播过程中入射角Ψ0逐渐增大,相应压力逐渐降低,可以通过马赫杆两侧爆轰产物流动基本方程及状态方程求出Ⅳ区的压力p4与Ψ0关系:
(3)
下面求解Ⅲ区爆轰波正规斜碰撞压力p3,当爆轰波作用于点F,穿入爆轰波阵面后产物以速度u1流入区域Ⅱ,发生角度为θ的折转。根据波阵面前后质量守恒和动量守恒方程可以得到:
(4)
式中:γ为炸药多方指数,一般取γ=3。Ψ1为正规斜碰撞入射角,即爆轰波在点F的切线与药型罩在点F的切线之间的夹角。当爆轰产物继续运动到反射波阵面,爆轰产物到达Ⅲ区的压力p3即为正规斜碰撞后的压力。由反射波阵面处守恒方程及相关几何关系可知:
(5)
式中:Ψ2为反射角。其中Ψ1、Ψ2与θ的关系可以表示为[11]:
(6)
爆轰波对药型罩的作用包括了罩顶部马赫压力作用区域及罩中部到口部部分受到的正规斜碰撞压力,根据马赫杆运动与药型罩的几何形状求解出2部分压力。
1.3 基于改进的PER理论杆式射流成形模型
根据伯努利方程可以求得药型罩微元形成的射流速度[12]:
(7)
式中:v为药型罩微元的绝对压垮速度,β为压垮角,λ为药型罩切线与轴线的夹角,δ为药型罩微元的偏转角。
绝对压垮速度v的计算采用兰德-皮尔森提出的速度历程曲线:
(8)
式中:T为爆轰波到达罩微元的时间,根据炸药的爆速及起爆点与微元距离计算;τ为时间常数,τ=A1mv0/pCJ+A2,A1、A2为常数,m为罩微元的质量。药型罩微元满足运动方程pS=Ft,将式(3)、(5)~(6)代入式(8)可得到:
(9)
式中:S为微元面积。由式(9)可以计算出不同区域药型罩微元极限压垮速度v0。偏转角δ也采用式(8)的形式,压垮角β、t时刻射流位置l、射流质量mj的求法如下:
(10)
(11)
(12)

2 计算结果分析
2.1 爆轰波对偏心亚半球罩作用规律分析

图3 马赫反射压力、正规斜反射压力和射流头部速度随药型罩结构参数的变化曲线Fig.3 Curves of Mach reflection pressure, regular oblique reflection pressure and tip velocity of jet vs. liner configuration parameters
成形装药的主、辅装药均采用8701炸药,炸药密度为1.71 g/cm3,爆速为8 425 m/s,CJ压力为29.5 GPa。图2中以点O为引爆源形成的爆轰波经过辅助炸药分别向主装药和隔板传播,爆轰波分别在主装药和隔板中绕射、透射,为了使绕射爆轰波到达点G处碰撞形成马赫超压并有效作用于药型罩,设计隔板结构时需要满足爆轰波绕射时间小于透射时间。隔板中波传播的速度为1 933 m/s,传播距离为35 mm,另外从点O到点G包括5 mm厚的辅助药柱,经计算求得的透射时间为18.6 μs。爆轰波绕射距离为OO1与O1G之和,通过计算得出绕射时间为14.2 μs。绕射时间小于透射时间,说明设计的隔板结构是合理的,可以保证爆轰波碰撞前不会受到透射波的干扰。将临界入射角处的压力、密度代入式(1),可以求得α=8°。BC到达药型罩顶部时产生的马赫压力将直接影响罩顶部区域的压垮速度,利用式(3)对马赫压力进行计算,得到图3(a)所示马赫反射压力随药型罩结构参数的变化曲线。
从图3(a)可以看出,偏心距a越大,罩顶处马赫压力越高,马赫压力随着rL的增大逐渐降低,并且马赫压力在90~100 mm快速下降,而在100~120 mm时平缓减小,随着rL的增大不同偏心距罩顶部马赫压力差距越来越小,这是因为rL越小,药型罩顶部距马赫杆初始形成点越近。将点F定为距离轴线25 mm,图3(b)为点F处正规斜碰撞压力随药型罩结构参数的变化曲线。根据图中计算结果可知,正规斜反射压力随药型罩结构参数的变化范围较小,随着rL的增大压力逐渐增大,而偏心距越小正规斜碰撞压力越大。
将求得的不同罩微元处压力代入式(9)求出极限压垮速度,利用式(6)求出射流速度,根据头部组合颗粒速度公式[12]计算出射流的头部速度,杆式射流头部速度vtip随罩结构参数变化如图3(c)所示,药型罩的厚度均取为2.2 mm。比较图3(a)、(c)可以看出,射流头部速度与马赫压力随药型罩结构参数变化规律一致。
当rL=90 mm、a=39 mm时射流头部速度最高,以此结构为例,计算药型罩各微元形成射流的质量,图4(a)为该结构药型罩形成的射流质量分布曲线,其中x为药型罩位置。药型罩微元从顶部变化到口部,罩质量及其形成射流质量均逐渐增大,罩质量增速逐渐变缓,而罩微元形成射流质量增速逐渐变快。将罩微元形成射流的质量除以罩微元质量可以得到各微元形成射流的百分比,从图4(a)可以看出,罩顶部与罩口部形成射流部分的百分比较大,而中间部分较小。图4(b)为该结构药型罩形成的射流速度分布曲线,包括各微元射流速度及头部组合颗粒速度,两条曲线的交点即为射流头部速度及其对应药型罩微元位置。射流头部质量堆积点距离药型罩顶部18.5 mm,占药型罩高度的27.3%,较单锥罩降低了约15%,使得更多微元形成有效射流,破甲作用将会增大。

图4 射流质量和射流速度分布曲线Fig.4 Curves of jet mass and jet velocity distribution
2.2 壁厚变化对杆式射流成形的影响
为了提高聚能杆式射流的侵彻能力,应该在等质量药型罩前提下,通过调整药型罩的壁厚,设计出能提高射流质量的药型罩结构。另外,通过增大速度梯度可以提高小炸高下聚能杆式射流的侵深。在方案A(rL=90 mm、a=39 mm、h=2.2 mm)等壁厚结构的基础上,对药型罩的内壁进行重新设计,如图5所示。
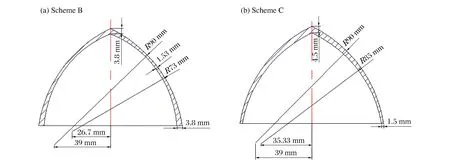
图5 变壁厚药型罩Fig.5 Variable thickness liners
图5为2种改进的变壁厚方案。方案B为罩顶与罩口部厚、中间薄药型罩,方案C的药型罩壁厚从罩顶到罩口部逐渐变薄。方案B的内壁曲率半径rL1=73 mm、内壁偏心距a1=26.7 mm、最大壁厚与最小壁厚分别为3.8、1.53 mm,方案C的rL1=85 mm、a1=35.33 mm、最大壁厚与最小壁厚分别为4、1.5 mm。
利用杆式射流成形理论计算了变壁厚药型罩形成射流的过程,获得了不同方案射流质量随药型罩位置的变化曲线,如图6(a)所示。当x在0~40 mm之间变化时,方案C形成射流质量最高,而方案B最低,但各方案相差较小。x在40~67 mm之间变化时,方案B形成射流质量显著高于其他方案。3种方案药型罩的初始质量均为320 g,对图6(a)中曲线进行积分处理,得到方案A~C射流质量分别为162.7、188.1、145.2 g,方案B的射流质量较方案C提高了29.5%。图6(b)为3种方案在2倍炸高处杆式射流速度分布曲线,方案B形成射流的头部速度最高,尾部速度最小,速度梯度最大,并且射流长度最大。综合分析射流质量及速度两方面性能,方案B形成的杆式射流成形参数最佳。

图6 不同方案射流质量随药型罩位置的变化曲线和射流速度分布曲线Fig.6 Curves of jet mass vs. liner position and jet velocity distribution for different schemes
利用LS-DYNA软件对3种方案的成形过程进行数值模拟,获得了2倍炸高处射流的成形形态及头尾速度。数值模拟中材料模型见文献[13-14],杆式射流成形计算结果如表1所示,其中vtip、vtail分别为杆式射流的头部速度和尾部速度。从成形形态可以看出,方案B的杵体明显小于其他2种方案,验证了理论计算中方案B的射流质量最大,理论计算的杆式射流头尾速度结果偏大,这是由于理论模型中没有考虑药型罩微元之间的相互作用,但模拟结果能够验证不同装药结构形成的毁伤元头尾速度变化趋势。

表1 杆式射流成形计算结果
3 侵彻威力实验验证
为了进一步验证不同结构形成杆式射流的作用性能,对上述3种方案开展了2倍炸高条件下侵彻钢靶的实验,成形装药实物如图7所示,同时利用LS-DYNA软件对杆式射流侵彻钢靶进行了数值计算。为了便于分析杆式射流的侵彻通道及破孔孔形,采用3层钢靶,材料为45钢。图8为方案B第1块靶的侵彻通道和第2块靶入口孔形,孔道较光滑,侵彻通道直径较均匀。图8还给出了侵彻模拟效果图,可以看出实验的侵彻通道及入口孔形与模拟结果吻合较好。

图7 成形装药实物图Fig.7 Photos of shaped charge

图8 侵彻通道及孔形Fig.8 Penetration channel and hole shape
表2为数值模拟与实验的侵彻结果对比,D1、D2、H分别为各块靶板的入孔直径、出孔直径、总侵深。从杆式射流侵彻能力方面可以看出方案B的优势较明显,穿深较方案C提高了约2倍装药直径,说明在药型罩质量不变的条件下,通过爆轰波波形与药型罩结构的合理匹配,能够增大杆式射流的质量及速度梯度,并将此优越性能体现在对目标的侵彻能力上,实现侵彻深度的提高。

表2 数值模拟与实验侵彻结果
4 结 论
利用爆轰波碰撞理论求解药型罩压垮速度,并结合改进PER理论建立了杆式射流成形模型。通过计算获得如下结论:
(1)理论研究了爆轰波碰撞压力随偏心亚半球药型罩结构参数的变化规律,马赫反射压力随偏心距的增大而增大,随外壁曲率半径的增大而减小,而正规斜反射压力与马赫反射压力变化规律相反,且马赫反射压力受药型罩结构影响较大。
(2)在等质量药型罩的前提下,通过调整罩内壁结构,得到了壁厚变化对射流质量及速度分布的影响规律。罩顶与罩口部厚、中间薄形状形成的射流质量提高了29.5%,头部速度提高了21.3%,且速度梯度最大,并利用数值模拟验证了其成形效果最佳。
(3)实验和数值模拟研究了杆式射流侵彻钢靶的过程,罩顶与罩口部厚、中间薄形状药型罩形成的射流侵深提高了约2倍装药直径。通过爆轰波波形与药型罩结构的合理匹配能够形成性能优越的杆式射流,可以显著提高战斗部的毁伤能力。
[1] 谭多望,孙承纬.成型装药研究新进展[J].爆炸与冲击,2008,28(1):50-56. Tan Duo-wang, Sun Cheng-wei. Progress in studies on shaped charge[J]. Explosion and Shock Waves, 2008,28(1):50-56.
[2] Church P, Cornish R, Cullis I, et al. Experimental and simulation studies of slow stretching jets[C]∥Reinecke W G. Proceedings of the 18th International Symposium on Ballistics. Lancaster: Technomic Publishing Co. Inc, 1999:474-483.
[3] Fong R. Warhead technology advancement[C]∥Armaments for the Army Transformation Conference. New Jersey: U. S. Army Armament Research, Development and Engineering Center, 2000:1-26.
[4] Blache A, Weimann K. Shaped charge with jetting projectile for extended targets[C]∥Niekerk C V. Proceedings of the 17th International Symposium on Ballistics. Midrand, South Africa: The South African Ballistics Organisation, 1998:207-215.
[5] Funston R J, Mattsson K V, Ouye N N. K-charge—A multipurpose shaped charge warhead[P]. USA: US6393991 B1, 2002-05-28.
[6] 黄正祥,张先锋,陈惠武.起爆方式对聚能杆式侵彻体成型的影响[J].兵工学报,2004,25(3):289-291. Huang Zheng-xiang, Zhang Xian-feng, Chen Hui-wu. Influence of modes of detonation on the mechanism of jetting projectile charge[J]. Acta Armamentarii, 2004,25(3):289-291.
[7] 吴晗玲,段卓平,汪永庆.杆式射流形成的数值模拟研究[J].爆炸与冲击,2006,26(4):328-332. Wu Han-ling, Duan Zhuo-ping, Wang Yong-qing. Simulation investigation of rod-like jets[J]. Explosion and Shock Waves, 2006,26(4):328-332.
[8] 王志军,伊建亚,张洪成,等.紧凑型聚能装药结构对侵彻体成型的影响[J].兵器材料科学与工程,2014,37(1): 53-56. Wang Zhi-jun, Yi Jian-ya, Zhang Hong-cheng, et al. Influence of compact shaped charge on penetrator formation[J]. Ordnance Material Science and Engineering, 2014,37(1):53-56.
[9] Muller F. Mach-reflection of detonation waves in condensed high explosives[J]. Propellants, Explosives, Pyrotechnics, 1978,3(4):115-118.
[10] 王继海.二维非定常流和激波[M].北京:科学出版社,1994:38-146.
[11] 张洋溢,龙源,何洋扬,等.爆轰波斜冲击金属介质理论在聚能装药药型罩设计中的应用研究[J].振动与冲击,2011,30(7):214-217. Zhang Yang-yi, Long Yuan, He Yang-yang, et al. Application of oblique impact theory of detonation waves at the explosive-metal interface in design of shaped charge[J]. Journal of Vibration and Shock, 2011,30(7):214-217.
[12] 王树魁,贝静芬.成型装药原理及其应用[M].北京:兵器工业出版社,1992:51-69.
[13] Livermore Software Technology Corporation. LS-DYNA keyword user’s manual[Z]. California: Livermore Software Technology Corporation, 2003.
[14] Li Wei-bing, Wang Xiao-ming, Li Wen-bin. The effect of annular multi-point initiation on the formation and penetration of an explosively formed penetrator[J]. International Journal of Impact Engineering, 2010,37(4):414-424.
(责任编辑 曾月蓉)
Effect of matching of detonation waveform with liner configuration on the rod-like jet formation
Chen Chuang, Wang Xiao-ming, Li Wen-bin, Li Wei-bing, Dong Xiao-liang
(MinisterialKeyLaboratoryofZNDY,NanjingUniversityofScienceandTechnology,Nanjing210094,Jiangsu,China)
To improve the steel target penetrating capability of the rod-like jet, we designed an eccentric semispherical liner. The liner’s collapsing velocity was deduced by detonation wave collision theory, and the rod-like jet formation model was established by combining the improved PER theory. The laws determining how the liner configuration parameters affect the detonation wave collision pressure were drawn out, and the jet mass and velocity distribution laws were obtained by changing the thickness of the equal mass liner. Our test results show that the Mach collision pressure increased with the increase of the eccentric distance, and decreased with the increase of the ectotheca curvature radius. Moreover, the variation law of the regular oblique reflection pressure was reverse with the Mach collision, which was greatly affected by the liner configuration. By comparing different schemes, we find that the jet mass of the liner, which was thick at the top and the bottom but thin in the middle, increased by 29.5%, and the tip velocity increased by 21.3%, while, with the maximum velocity gradient and the same condition of standoff distance, the penetration depth almost doubled the charge caliber. The simulation and experiment were carried out aiming at the optimal configuration, and the formation and penetration performance of the rod-like jet was improved remarkably through the optimum matching of the detonation wave form with the liner configuration.
mechanics of explosion; rod-like jet; penetration; detonation waveform; eccentric semispherical liner
10.11883/1001-1455(2015)06-0812-08
2014-04-17;
2014-08-26
国家自然科学基金项目(11202103)
陈 闯(1987— ),男,博士研究生,chenchuang517@126.com。
O381 国标学科代码: 13035
A
