一种与爆轰参数封闭的JWL方程参数确定方法*
2015-04-12南宇翔蒋建伟王树有门建兵
南宇翔,蒋建伟,王树有,门建兵
(北京理工大学爆炸科学与技术国家重点实验室,北京 100081)
一种与爆轰参数封闭的JWL方程参数确定方法*
南宇翔,蒋建伟,王树有,门建兵
(北京理工大学爆炸科学与技术国家重点实验室,北京 100081)
利用数值模拟和理论计算分析了炸药JWL状态方程参数与爆轰参数封闭的重要性;获得了利用圆筒实验测试结果计算炸药爆轰产物绝热等熵指数和爆压的方法;建立了与爆轰参数封闭的JWL状态方程参数的确定方法,并依据公布的圆筒实验数据,应用于两种典型炸药JWL状态方程参数的确定,获得的参数与炸药爆轰参数严格封闭,数值模拟结果与实验结果一致性好,表明炸药JWL参数确定方法合理可靠。
爆炸力学;参数确定;约束守恒;JWL状态方程;圆筒实验
JWL状态方程是描述炸药爆轰产物做功能力的一种形式,在炸药爆轰及爆炸驱动的数值模拟中被广泛采用[1-2],JWL方程中含有A、B、R1、R2、ω、E0(等熵形式时为C)等6个参数。J.W.Kury等[3]首先提出应用标准圆筒实验确定炸药JWL方程参数的方法,并公布了典型炸药的JWL方程参数,这些炸药的JWL参数与炸药爆轰参数(爆速、爆压、爆热等)存在封闭性[4],即只要已知JWL的6个参数和密度就可获得炸药爆轰参数。JWL状态方程参数的确定除借助圆筒实验结果外,还需CHEETCH、CHEQ等专用处理软件[5],关于软件方法则未见公开。叶早发等[6]采用数值模拟方法研究了JWL方程每个参数对圆筒壁驱动速度的影响规律,给出了已知圆筒实验和爆轰参数条件下,采用分段确定R1、R2、ω参数获得JWL参数的方法,该方法忽略了3个参数间的协调变化。《标准圆筒试验法》1991年公布,至1997年有了修订版GJB 772A-97[7],但未形成操作性强的JWL参数确定方法,目前主要是在圆筒实验基础上以“凑参数-数值模拟”重复循环过程为主,这种“试错法”靠经验调整6个参数,拟合过程复杂,参数拟合结果因人而异。一些炸药JWL参数[8-11]的选定注重了数值模拟的圆筒壁驱动速度曲线和膨胀位移曲线与实验结果误差控制在一定范围,忽略了JWL方程参数与炸药爆轰参数的封闭性,导致计算的爆速、爆压与实验误差大,显然,将直接影响数值模拟中炸药爆轰及驱动结果的可靠性。
本文中,推导并分析JWL状态方程与炸药爆轰参数封闭的重要性,提出基于炸药圆筒实验确定等熵指数和爆压的计算方法,建立考虑JWL方程参数与爆轰参数封闭的JWL方程参数确定方法,该方法比“试错法”增加了爆轰产物在CJ状态的约束条件判断,可消除人为拟合JWL方程参数的多样性,可有效缩短参数确定的周期。
根据典型RDX基及HMX基炸药圆筒实验结果,采用本文方法确定这两种炸药的JWL参数,将所得的JWL状态方程参数的数值模拟结果与圆筒实验结果比较,考察参数是否合理。
1 炸药JWL参数与爆轰参数封闭的重要性分析
常见的JWL方程的压力和等熵形式为[12]:
(1)
(2)
根据炸药爆轰理论,在理想爆轰时炸药爆轰产物在CJ状态满足约束守恒方程组[4]:
(3)

在已知炸药密度ρ0和JWL方程参数A、B、R1、R2、ω、E0下,采用MATLAB软件求解方程组(3),可得到炸药爆速D、爆压pCJ和爆热Qe。
图1为∅25mm×300mm标准圆筒计算模型。沿炸药轴线不同位置处设置观测点1~17,无氧铜管壁面设置观测点18(距起爆端200mm)。

图1 圆筒模型及测量点位置Fig.1 Cylinder model and gauge position
由文献[10]可知,典型RDX基炸药JWL方程参数分别为:ρ0=1.65g/cm3,D=8.19km/s,pCJ=27.67GPa,A=640GPa,B=17.6GPa,R1=4.5,R2=1.35,ω=0.30,E0=11.56J/mm3。将炸药的JWL参数代入式(3),反推得到爆速、爆压和爆热的计算值分别为:Qc=7.006kJ/g,Dc=8.596km/s,(Dc-D)/D=4.96%,pc=33.15GPa,(pc-pCJ)/pCJ=19.80%。
应用LS-DYNA软件对圆筒的炸药爆炸驱动过程进行数值模拟,图2为获得的观测点18处圆筒壁的速度曲线,图3为不同位置处的爆轰压力曲线。
从图2可以看出,数值模拟与实验测试结果吻合较好,但在图3中,压力峰值大于炸药CJ爆压,其原因是爆轰参数计算结果与实际爆速D、爆压pCJ有较大的差异所致。可见,炸药JWL方程参数与爆轰参数不封闭会影响数值模拟计算的准确性。

图2 圆筒壁速度曲线Fig.2 Velocities of cylinder wall

图3 观测点压力曲线Fig.3 Pressures of different gauge points
2 炸药JWL状态方程参数确定方法
2.1 输入参数的确定

(4)
上式中需已知爆压pCJ,考虑爆压pCJ测试的困难,以下提出了利用圆筒实验测试结果求解γ和pCJ的计算方法。
根据炸药圆筒实验数据处理方法[13],从圆筒实验高速摄影图像可获得筒壁膨胀位移曲线(见图4),拟合出圆筒壁质量中心面的多项式膨胀位移表达式:
(5)
式中:aj、bj为待定系数,ti=t+ t0,一般取n=2。
根据质量、动量守恒可计算出爆轰产物的压力-相对比容关系(见图5),为γ律方程:
(6)
应用最小二乘法可拟合出a、γ值,将拟合出的γ值作为CJ状态时的γ值,根据式(3)就可得到pCJ。

图4 圆筒实验膨胀位移曲线Fig.4 Expansion displacement curves of cylinder wall

图5 压力与相对比容的关系Fig.5 Pressure vs. relative volume

图6 JWL方程参数确定方法流程Fig.6 The methodology process for obtaining JWL parameters
2.2 参数确定方法和流程
图6为基于圆筒实验的JWL方程参数确定方法总流程图,增加了CJ约束方程的判断,基本消除了JWL方程参数的多样性。主要步骤为:
(1)参数E0的确定。E0为单位体积炸药的初始总能量,表征炸药可对外做功的总能量,E0=ρ0Qe,其中Qe是炸药实测爆热,也可用理论爆热Qt代替。

(3)参数R1、R2的设定。R1、R2是与爆轰产物膨胀的高压段和中压段有关的系数,是参数确定过程中可以进行调整的驱动参数。通常认为:4≤R1≤7,0.8≤R1≤2。一般设定初始值:R1=4.5,R2=1.5。
(4)参数A、B参数的确定。已知ρ0、D、γ、R1、R2、ω、E0,可通过爆轰产物CJ态守恒方程组(3),计算A、B、C的值,这样JWL方程的6个参数与炸药爆轰参数之间可以形成严格封闭。A、B、C的约束条件为:A,B,C>0,A≈(10~100)B,B≈(10~100)C。若不符合,需要先调整R1、R2值,直到符合为止,再进行下一步计算。
(5)参数的校验与调整。采用以上计算获得的JWL参数,使用AUTODYN、LS-DYNA等软件模拟标准圆筒实验。得到与实验相同观测位置处圆筒壁径向的速度和膨胀位移曲线,并对比实验结果。

(7)
若数值模拟的结果在(R-R0)为19 mm的比动能与实验结果基本一致,但(R-R0)为6、12.5及25 mm时比动能偏离过大,则适当调整ω值,再调整R1、R2。ω越大,速度曲线越陡峭。最终得到满足误差要求的JWL方程参数。
3 方法的应用
为验证本文确定方法的可靠性,应用文献[10]中的典型RDX基炸药圆筒实验数据进行JWL方程参数的确定。为检验本文中JWL参数确定方法的适用性,应用已知的圆筒实验结果确定典型HMX基炸药JWL参数。
3.1 典型RDX基炸药
应用本文方法,典型RDX基炸药的JWL方程参数分别为:ρ0=1.65 g/cm3,A=937.29 GPa,B=16.279 GPa,R1=5.2,R2=1.0,ω=0.43,E0=8.5 J/mm3。
经式(3)得到爆速Dc、爆压pc和爆热Qc分别为:Dc=8.19 km/s,γc=3.0,pc=27.67 GPa,Qc=5.152 kJ/g,与炸药实际参数严格封闭。

表1 数值模拟与实验结果对比Table 1 Results of experiment and simulation
表1为采用两套参数进行数值模拟获得的圆筒壁速度及比动能,其中为验证JWL参数对于不同计算程序的适用性,分别使用LS-DYNA(本文1)和AUTODYN(本文2)程序进行计算。图7为圆筒壁速度曲线和膨胀位移曲线。

图7 数值模拟与实验结果曲线Fig.7 Curves of simulation and experiment

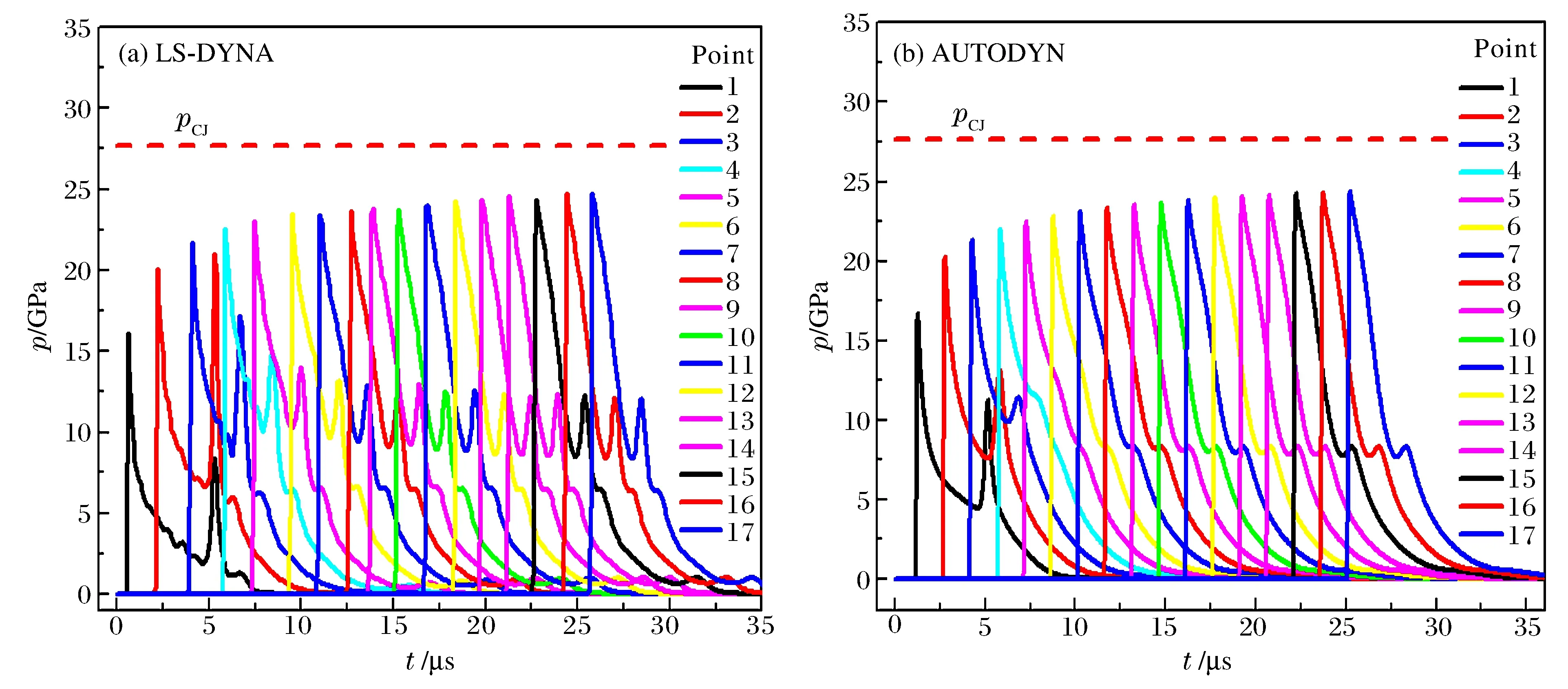
图8 应用本文JWL参数的圆筒压力曲线Fig.8 Pressure curves of different gauge point by using new JWL parameters
3.2 典型HMX基炸药
已知某典型HMX基炸药密度为1.831 g/cm3,爆速为8 740 m/s,此外仅有25 mm圆筒实验测试点处的圆筒壁速度和膨胀位移曲线。应用本文方法获得的JWL参数分别为:ρ0=1.831 g/cm3,A=888.88 GPa,B=19.854 GPa,R1=4.69,R2=1.30,ω=0.28,E0=10 J/mm3,Dc=8.740 km/s,γc=2.885,pc=36.0 GPa,Qc=5.461 kJ/g,经式(3)得到的Dc与炸药实际参数严格封闭。
表2为应用LS-DYNA和AUTODYN软件进行数值模拟计算的结果,与实验测试结果一致性好,均满足误差要求,获得的JWL参数合理可靠,这证明了本文方法确定炸药JWL参数的可靠性。

表2 数值模拟与实验结果对比Table 2 Results of experiment and simulation
4 结 论
通过研究典型炸药JWL参数对数值模拟结果的影响,分析了JWL参数与爆轰参数封闭的重要性;建立了一套可操作的理想爆轰的炸药JWL状态方程参数确定方法,该方法利用圆筒实验确定了爆轰产物绝热等熵指数和爆压,同时增加了爆轰产物CJ态约束守恒判断,获得的炸药JWL参数与爆轰参数严格封闭;应用圆筒实验结果,采用本文参数确定方法获得了RDX基及HMX基典型炸药JWL状态方程参数,所得参数与炸药爆轰参数严格封闭,圆筒数值模拟结果与实验一致性好。本文的炸药JWL参数确定方法比现有的“试错法”更准确地描述炸药爆轰及驱做功能力。此方法可为快速准确确定炸药爆轰产物JWL状态方程参数提供参考。
[1] 奥尔连科.爆炸物理学[M].孙承纬,译.北京:科学出版社,2011:118-122.
[2] 陈朗,冯长根,黄毅民.含铝炸药圆筒试验及爆轰产物JWL状态方程研究[J].火炸药学报,2001,24(3):13-15. Chen Lang, Feng Chang-gen, Huang Yi-min. The cylinder test and JWL equation of state detonation product of aluminized explosives[J]. Chinese Journal of Explosives & Propellants, 2001,24(3):13-15.
[3] Kury J W, Hornig H C, Lee E L, et al. Matel acceleration by chemical explosives[C]∥Proceedings of the 4th International Symposium on Detonation. White Oak, Maryland, 1966:3-13.
[4] Souers P C, Wu B, Haselman L C. Detonation equation of state at LLNL[R]. CA: Lawrence Livermore National Laboratory, 1996.
[5] Dobratz B M, Crawford P C. LLNL explosives handbook[R]. CA: Lawrence Livermore National Laboratory, 1985.
[6] 叶早发,刘汉彬,朱光馨,等.利用DYNA程式进行JWL 状态方程式之参数计算[J].火药技术,2004,20(1):35-48.
[7] GJB 772A-97 标准圆筒试验法[S].1997.
[8] 陈清畴,蒋小华,李敏,等.HNS-IV炸药JWL状态方程研究[J].火工品,2010(4):21-24.
[9] 孙占峰,徐辉,李庆忠,等.钝感高能炸药爆轰产物JWL状态方程再研究[J].高压物理学报,2010,24(1):55-60. Sun Zhan-feng, Xu Hui, LI Qing-zhong, et al. Further study on JWL equation of state of detonation product for insensitive high explosive[J]. Chinese Journal of High Pressure Physics, 2010,24(1):55-60.
[10] 陈清畴,蒋小华,李敏,等.RDX基高聚物粘结炸药JWL状态方程[J].含能材料,2011,19(2):213-216. Chen Qing-chou, Jiang Xiao-hua, Li Min, et al. JWL equation of state for RDX-based PBX[J]. Chinese Journal of Energetic Materials, 2011,19(2):213-216.
[11] 于川,刘文翰,李良忠,等.RHT-902和Octol炸药爆轰产物JWL状态方程研究[J].爆炸与冲击,1993,13(2):172-177. Yu Chuan, Liu Wen-han, Li Liang-zhong, et al. Studies on the JWL equation of state of detonation products for RHT-902 and Octol[J]. Explosion and Shock Waves, 1993,13(2)172-177.
[12] Lee E L, Hornig H C, Kury J W. Adiabatic expansion of high explosive detonation products[R]. CA: Lawrence Livermore National Laboratory, 1968.
[13] 孙占峰,李庆忠,孙学林,等.标准圆筒试验技术与数据处理方法研究[J].高压物理学报,2008, 22(2):160-166. Sun Zhan-feng, Li Qing-zhong, Sun Xue-lin, et al. Study on standard cylinder test technology and data processing method[J]. Chinese Journal of High Pressure Physics, 2008,22(2):160-166.
[14] 爆炸及其作用[M].北京:科学出版社,2011:130-131.
[15] 孙承纬,卫玉章,周志奎.应用爆轰物理[M].北京:国防工业出版社,2000:295-296.
(责任编辑 丁 峰)
One parameter-obtained method for JWL equation of state considered detonation parameters
Nan Yu-xiang, Jiang Jian-wei, Wang Shu-you, Men Jian-bing
(StateKeyLaboratoryofExplosionScienceandTechnology,BeijingInstituteofTechnology,Beijing100081,China)
In this paper, the method of obtaining parameters for JWL equation of state is investigated. The importance of JWL parameters considered detonation parameters is analyzed using simulation and theoretical calculation. Isentropic adiabatic index and detonation pressure of detonation product are calculated according to cylinder test. The methodology process for obtaining JWL parameters of ideal detonation product considered detonation parameters is established. The JWL parameters of two typical explosive are obtained with the application of this method according to published cylinder experimental result. The results of numerical simulation agree with the cylinder test so that the JWL parameters are reasonable and reliable.
mechanics of explosion; parameter-obtained; self-closing constraint; JWL equation of state; cylinder experiment
10.11883/1001-1455(2015)02-0157-07
2013-07-23;
2013-10-28
国家自然科学基金项目(11032002);国家重点基础研究发展计划(973计划)(2010CB832706); 爆炸科学与技术国家重点实验室基金项目(ZDKT-1102)
南宇翔(1988— ),男,博士研究生,nyxbaboon@126.com。
O389;TJ45 国标学科代码: 1303510
A
