硅油风扇离合器滑差和散热性能的计算与测试*
2015-04-12上官文斌宋黎明贺频燕段耀龙竺菲菲
上官文斌,宋黎明,贺频燕,段耀龙,竺菲菲
(1.华南理工大学机械与汽车工程学院,广州 510641; 2.雪龙集团股份有限公司,宁波 315800)
2015122
硅油风扇离合器滑差和散热性能的计算与测试*
上官文斌1,2,宋黎明1,贺频燕2,段耀龙2,竺菲菲2
(1.华南理工大学机械与汽车工程学院,广州 510641; 2.雪龙集团股份有限公司,宁波 315800)
以一双面槽型硅油风扇离合器为研究对象,考虑硅油黏度随剪切半径而变化,建立了硅油离合器传递转矩和散热量的计算模型。利用建立的模型计算分析了硅油风扇离合器滑差和壳体表面温度随输入转速的变化。同时构建了硅油风扇离合器试验台,进行相应的测试。计算结果与试验数据基本一致,验证了模型的正确性。最后,利用所建模型,计算了其它6款硅油风扇离合器的滑差和壳体表面温度,并与试验结果进行了对比分析。
硅油风扇离合器;滑差;散热性能;计算;测试
前言
19世纪60年代博格华纳制造出了世界上第一台硅油风扇离合器。与传统的冷却风扇相比,硅油风扇离合器可根据控制温度的要求,自动调节风扇转速,使发动机在最佳工作温度下工作,因此具有节能、降噪、减排和延长发动机寿命等优点。硅油风扇离合器的性能以滑差率和散热性能来衡量,其中滑差率为滑差(输入与输出转速的差)除以输入转速的百分比,滑差率一般要求在3%~7%范围。
关于硅油风扇离合器滑差和散热性能计算方面的文献较少,国外的研究侧重其控制系统部分和发动机冷却系统整体性能与经济性的研究[1-3],国内的研究工作开始较晚,文献[4]和文献[5]中建立了硅油离合器传递转矩的数学模型和计算公式,但没有考虑硅油动力黏度随剪切半径而变化的问题,且给出的应用实例较少。
本文中以一款双面槽型硅油风扇离合器为研究对象,测试了该离合器的滑差和壳体表面温度随输入转速的变化;考虑硅油动力黏度随剪切半径变化,建立了硅油离合器传递转矩和散热的计算模型,利用该模型计算分析了滑差和壳体表面温度随输入转速的变化。计算结果和实测值基本一致,证明了模型的正确性。最后对其它6款硅油风扇离合器的性能进行了计算分析,计算结果验证了本文中建立模型的正确性和实用性。
1 硅油风扇离合器传递转矩的计算模型
本文中研究的双面槽型硅油风扇离合器如图1所示,离合器主、从动板剪切工作面形状是矩形槽,由圆环面剪切面和圆柱面剪切面两部分构成。在离合器进入工作状态时,硅油将充满剪切面间隙。
硅油运动黏度γs(m2/s)随着温度Ts(℃)的升高按幂指数的规律降低,其关系[4]为
γs=γ0e-λ(Ts-T0)
(1)
式中:T0为环境温度;γ0为硅油在T0时的运动黏度;λ为黏温指数,试验测得硅油的黏温指数为0.018 69。
硅油密度随温度的升高而稍有减小,硅油温度从50升高到90℃时,硅油密度由0.95减小到0.92g/cm3,变化很小,因此硅油离合器在正常工作情况下可假设硅油密度为定值。根据硅油动力黏度μs与相同温度下硅油运动黏度γs和密度ρs的关系,即μs=ρsγs=ρ0γs,由式(1)得
μs=μ0e-λ(Ts-T0)
(2)
式中μ0为硅油在T0时的动力黏度,工程上通常测试离合器硅油在25℃时的动力黏度。
剪切油槽半径r处1min剪切的路径长度l与剪切半径r和剪切转速n的关系为
l=2πnr
(3)
硅油离合器圆环面与圆柱面剪切面间隙一般为0.3~0.6mm,间隙比较小,不利于硅油的流动散热,所以不同剪切半径处硅油温度不同,硅油动力黏度随剪切半径变化而变化。假设剪切油槽里硅油动力黏度为半径的函数[6],即
(4)
式中:μsa和μsc分别为圆环面和圆柱面剪切面间隙中的硅油动力黏度;μsmin为最小剪切半径rmin处硅油的动力黏度(硅油温度为Tsmin时),设为基准黏度;aa、ba为圆环面剪切面液体系数,ac、bc为圆柱面剪切面液体系数,是和油膜厚度相关的常数,aa,c+ba,c/rmin=1。若aa或ac已知,根据aa,c+ba,c/rmin=1,可求ba或bc。不同结构的离合器,aa、ac不同,先根据实测结果或者工程经验调试出一款离合器的aa、ac,然后再使用文中建立的模型去计算分析离合器性能。对本文中研究的6款离合器产品,由试验得到的aa、ac的取值范围为-0.7~-1.2。
1.1 圆柱坐标系下传递转矩的一般计算公式
硅油离合器靠硅油传递转矩,建立圆柱坐标系如图2所示。图中的圆环面微元面积dAa和圆柱面微元面积dAc传递的转矩dMa和dMc[4]分别为
(5)
式中:ur、uθ、uz分别为硅油的径向、周向和轴向流速。
在硅油风扇离合器中,可近似认为硅油的流动是轴对称的,即流速与转角θ无关,则式(5)简化为
(6)
1.2 圆环面剪切面传递转矩的数学模型
硅油在主动板和从动板间流动时,圆环面剪切面可简化为如图3所示的情形。
假定硅油周向流速沿z轴为线性分布[4],得到
(7)
式中:ω1、ω2分别为主、从动板角速度;h为圆环面剪切面间隙。
将式(4)代入式(7)并积分,求得圆环面油膜从剪切半径Ri到Ro之间的传递转矩Ma[6]为
(8)
1.3 圆柱面剪切面传递转矩的数学模型
圆柱面剪切面可简化为半径为ri、ro套在一起的圆筒,两者分别以角速度ω1、ω2绕z轴旋转,外圆筒内壁与内圆筒外壁之间充满硅油,油膜宽度为L,如图4所示。
设油膜中半径r处的硅油角速度为ω,周向流速为uθ,则有
uθ=ωr
(9)
(10)
将式(10)代入式(6)并积分,求得宽度为L的圆柱面油膜所传递的转矩为
(11)
将式(4)代入式(11),得到
(12)
对式(12)两边进行积分,得到圆柱面油膜所传递的转矩Mc为
(13)
1.4 双面槽型硅油离合器传递转矩的一般计算公式
双面槽型硅油离合器工作示意图如图5所示。硅油风扇离合器工作室可分为若干个圆环面剪切面传递转矩模型和圆柱面剪切面传递转矩模型。由主从动盘的角速度与转速的关系式ωi=πni/30,i=1,2,以及式(8)和式(13),可得硅油风扇离合器传递转矩为

(14)
式中:N1、N2分别为圆环面剪切面、圆柱面剪切面个数;n1、n2分别为输入、输出转速;hi为第i个圆环面剪切面间隙;Lj为第j个圆柱面剪切面油膜宽度;Ri,i、Ro,i分别为第i个圆环面剪切面的内半径、外半径;ri,j、ro,j分别为第j个圆柱面剪切面的内半径、外半径。
式(14)中输入转速n1与输出转速n2的差可用Δn表示,即Δn=n1-n2,本文中将Δn定义为滑差,滑差Δn除以输入转速n1的百分比定义为滑差率。
对于含多对剪切槽的硅油离合器,不考虑回油槽的影响,其传递的转矩M可按式(14)计算。考虑回油槽影响时,设离合器主、从动盘上没有回油槽时总的黏性剪切面积为S1,加工出回油槽后总剪切面积减少了S2,令转矩修正系数η=S2/S1(范围5%~15%),则离合器传递转矩的修正值M′为
M′=(1-η)M
(15)
当硅油离合器输入转速为n1且达到稳定工作状态时,经过一段时间,输出转速n2、硅油与壳体表面温度和最小剪切半径处硅油温度Tsmin都不再变化。根据力矩平衡,风扇驱动转矩Mf与离合器传递转矩的修正值相等,即
Mf(n2)=M′(n2,Tsmin)
(16)
工程上,通常测试一些特定转速下的风扇驱动转矩和流量,根据这些测试得到的数据,通过数据拟合的方法,可以得到风扇在其它转速下的驱动转矩、流量与输出转速的函数关系。
2 硅油风扇离合器传热的数学模型
当硅油风扇离合器工作时,剪切面间隙中的硅油处于油膜剪切工作状态,其主、从动板间存在转速差(滑差),导致硅油内部产生大量的剪切热,这些热量会通过壳体传给周围空气。热量交换依次为硅油与壳体内表面的对流换热、壳体导热和壳体外表面与周围空气的对流换热,这3部分热交换传导的热量达到稳定并都与硅油产生的剪切热相等时,硅油风扇离合器进入平稳工作状态。
建立硅油风扇离合器传热的数学模型时,由于全部使用温度差计算传热,并且摄氏温度更直观,故温度单位全部为摄氏度。
2.1 离合器滑差产生的热量
硅油风扇离合器在工作时,因主、从动件间存在滑差而产生的热量Q1[4]为
Q1=πKM′(n1-n2)/30
(17)
式中K为热效率转化常数,经验值,取0.9。
2.2 硅油与壳体内表面对流换热
硅油与离合器壳体内表面的热交换系数非常大,因此在硅油风扇离合器稳定工作状态下,硅油温度Ts与离合器壳体内表面温度Tin非常接近,在计算模型中,假设两者相等:
Ts=Tin
(18)
本文中以最小剪切半径处硅油温度Tsmin作为壳体内表面平均温度Tin。
2.3 壳体导热分析
硅油风扇离合器壳体外表面结构复杂,均布的三角肋结构起加强散热作用,为方便计算做出以下假设:
(1) 硅油风扇离合器在稳定工作状态,壳体内是稳定的热传导状态;
(2) 壳体内表面温度Tin均相等,外表面温度Tout也均相同。
则壳体传导的热量Q2[4]为
Q2=λ1A(Tin-Tout)/δ1
(19)
式中:λ1为导热系数,壳体使用ADC12铝合金,取96.2W/(m·K);A为离合器壳体表面积,与散热肋表面积相差不大,文中以散热肋表面积A2代替计算;δ1为壳体平均厚度,取0.005m。
2.4 离合器壳体外表面与外界空气的换热
硅油风扇离合器在工作时,由于轴流式风扇的作用,其周围空气主要是轴向运动,其次是旋转运动。壳体与外界空气的对流散热比较复杂,为了计算方便,简化为4部分:(1)气流向圆盘垂直流动时,圆盘与空气的换热;(2)圆盘在空气中旋转时与空气的换热;(3)壳体对空气的辐射换热;(4)肋片传热。
(1) 气流向圆盘流动时,圆盘与空气的换热
当气流向圆盘流动时的情形如图6所示。圆盘与气流的对流换热系数αc1[4]为
(20)
其中v=4qf/[π(Df22-Df12)]
式中:D为离合器壳体直径;Re为雷诺数;λ2为导热系数,取0.024W/(m·K);Pr为普朗特常数,取0.7;γ为空气运动黏度,在标准大气压下25℃时,约为1.5×10-5m2/s;v为空气流速;qf为由风扇性能参数拟合所得的空气流量值;Df1为风扇轮毂直径;Df2为风扇外径。
(2) 圆盘在空气中旋转时与空气的换热
当圆盘在空气中旋转时的情形如图7所示。圆盘与气流的对流换热系数αc2[4]为
(21)
其中:Re=ωR2/γ
Gr=[9βR3π1.5(Tout-Tair)]/γ2
式中:R为圆形平板的半径,取为离合器壳体半径值,为0.5D;Gr为葛拉晓夫数;ω为离合器壳体即输出角速度值,ω=πn2/30;β为空气体积膨胀系数,β=2/(Tout+Tair+546);Tout为壳体外表面温度;Tair为空气环境温度。
(3) 离合器壳体与外界空气的辐射换热
硅油风扇离合器与外界空气辐射换热系数αR[5]为
(22)
其中Tm=(Tout+Tair)/2+273
式中:Tm为定性温度。
(4) 肋片传热分析
硅油风扇离合器外表面加装有大量的三角形剖面直肋(见图8),以利于增强硅油风扇离合器的散热,提高硅油风扇离合器的性能,肋效率ηf定义为肋片的实际传热量与理想传热量的比[5]。
影响肋效率的因素有:肋片材料导热系数λ1、肋片表面与周围空气间的导热系数λ2、肋片的几何尺寸(h和δ,见图9)。三角形剖面直肋的肋效率计算较为复杂,为了计算方便,可通过肋的尺寸参数计算h3/2(λ2/λ1Am)1/2,然后从图9(b)中查得肋效率[5],其中Am表示肋片截面积,Am=δh。本文中硅油离合器三角形剖面直肋效率为0.93。
(5) 离合器壳体与外界空气换热总量
硅油风扇离合器与空气的对流换热、辐射换热总热量Q3为
Q3=(αc1+αc2+αR)(A1+ηfA2)(Tout-Tair)
(23)
式中:A1为离合器等效圆盘前后面面积和,A1=πD2/2;A2为离合器散热肋表面积。
当硅油离合器输入转速n1达到稳定时,经过一段时间,输出转速n2不再变化,硅油和壳体表面温度不再变化。因此,存在唯一的最小剪切半径处硅油温度Tsmin及输出转速n2使离合器由于滑差产生的热量、壳体导热和离合器壳体外表面与外界空气的换热三者相等,即
Q1(n2,Tsmin)=Q2(Tsmin)=Q3(n2,Tsmin)
(24)
3 滑差及壳体表面温度的计算流程
利用建立的硅油风扇离合器传递转矩和传热数学模型计算离合器的滑差、离合器壳体表面的温度值和硅油温度最大值的流程如图10所示。
4 硅油风扇离合器性能实测及与计算结果的对比分析
4.1 测试方法
硅油风扇离合器性能测试试验台示意图如图11所示。通过变频器控制电机转速模拟输入转速,通过热风筒提供热风来模拟迎风情况;由主轴转速传感器测量输入转速,由红外线转速传感器测量输出转速,由温度传感器测量迎风温度,由红外线测温仪测量硅油离合器壳体表面温度。
(1) 滑差测试 在1 000~2 800r/min转速区间内,对一给定的输入转速,待输出转速稳定后,继续运转几分钟,然后测试输出转速和离合器壳体表面温度。测试过程中设置热风温度为60℃,以保证离合器完全啮合。
(2) 温度测试 在离合器壳体表面确定9个测温点,具体位置如图12所示。测温点1、2、3和7在散热肋上,测温点4、5、6、8和9夹在散热肋里。实测过程中待电机停转后,立即依次测试测9个测温点的温度值。
4.2 测试结果与分析
(1) 滑差 多次测试,并求均值,得到给定输入转速下的输出转速、滑差及滑差率,测试结果见表1。由表1可知,随着输入转速的提高,滑差率逐渐变大。
(2) 温度 多次测试并求均值,测试得到给定输入转速下的离合器壳体表面温度值如表2所示。由表2可知,随着输入转速的提高,壳体表面温升明显。另外表2中的平均值将作为壳体表面平均温度值。
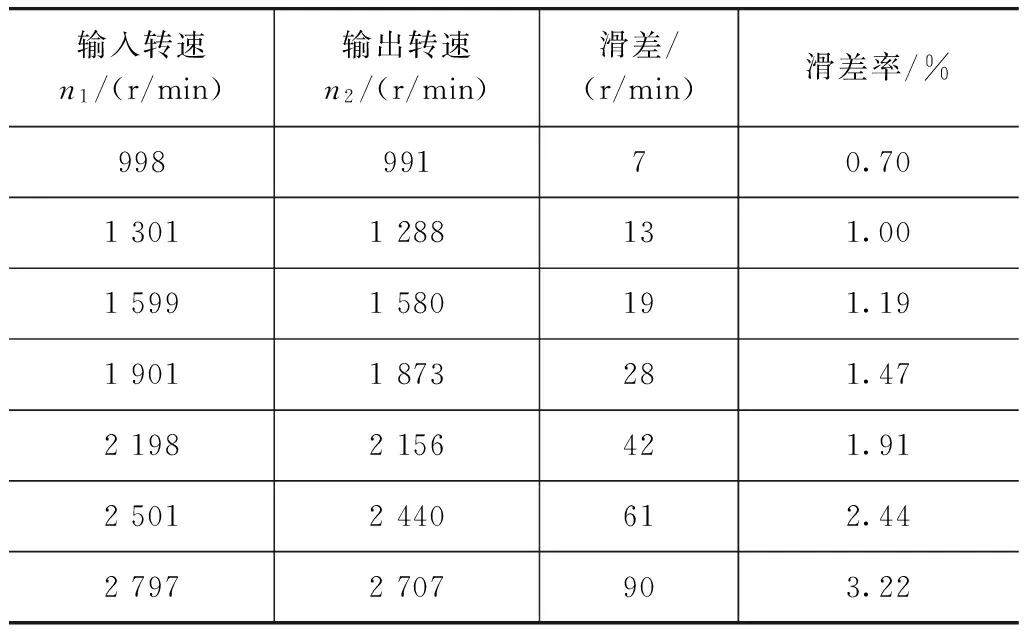
表1 输入、输出转速和滑差率
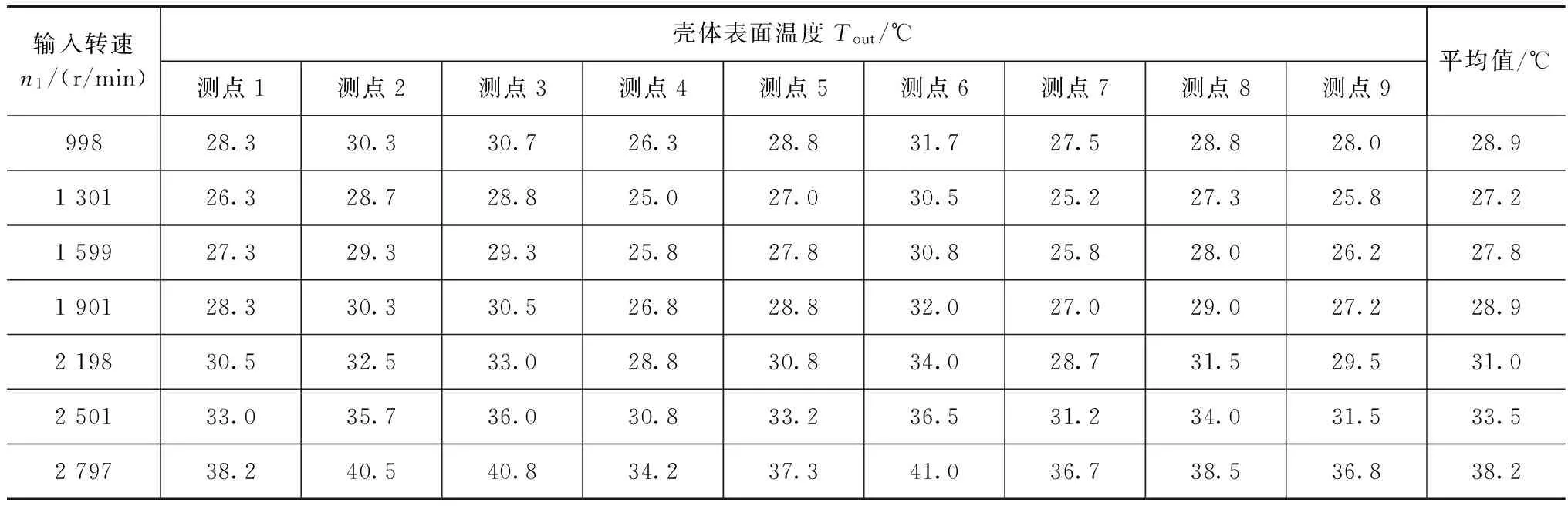
表2 离合器壳体表面温度值
4.3 滑差、壳体表面温度计算与实测对比
根据所建立的数学模型,编制计算程序来计算硅油离合器的滑差和壳体表面温度等参数,计算结果与实测结果的比较如图13和图14所示。
由图13和图14可见,硅油离合器滑差计算值与实验值相比稍大,壳体表面温度计算值与实验值相比稍小。工程上,即便同款离合器的滑差率也存在差异,波动区间在2%左右,所以总体上计算值与实验值比较一致,证实了本文建立的理论模型的正确性。
工作腔中硅油温度的最大值在最大剪切半径处,计算得到的硅油温度最大值如图15所示。
离合器硅油的安全使用温度一般在180℃以下,由图15可知硅油最高温度在100℃左右,满足要求。
4.4 应用
根据文中建立的计算模型,结合实测数据,即可调试得到离合器的液体系数。工程实际中,离合器数量远远少于风扇数量,如想获取所有离合器液体系数,工作量也不会很大。
表3为3个系列6款离合器性能的实测与计算值。同一系列中的两款离合器的结构完全相同,硅油黏度或者输入转速有差别。由表3可知,如果离合器输入转速较高,而所使用的硅油动力黏度又较低,则该款离合器的滑差率会比较大。
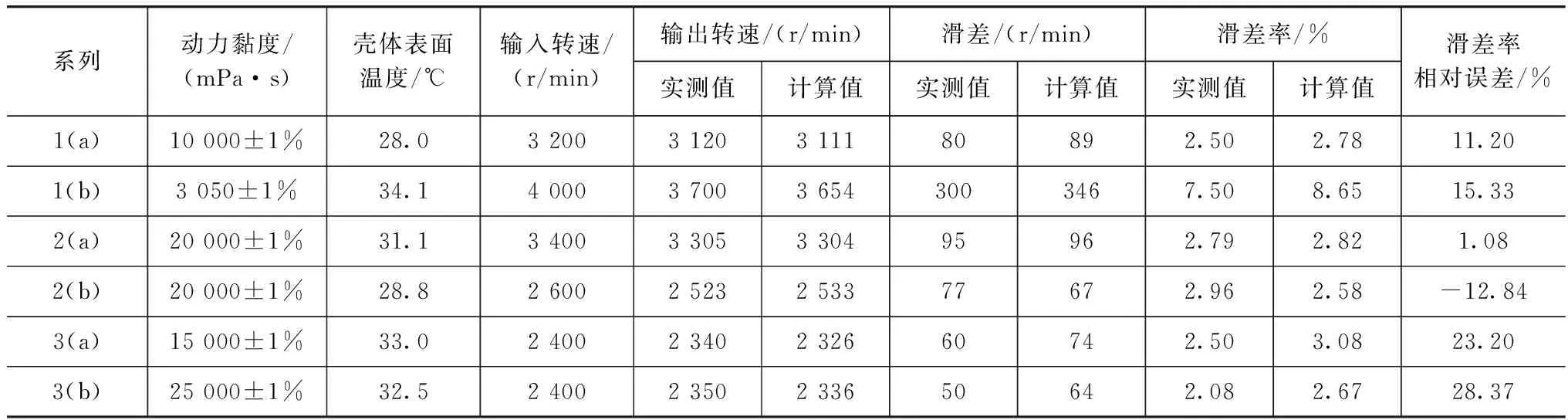
表3 离合器性能实测与计算结果
5 结论
以一款双面槽型硅油风扇离合器为研究对象,考虑了硅油黏度随剪切半径变化,建立了硅油离合器传递转矩和散热热量计算的模型。利用该模型计算分析了一款硅油风扇离合器的滑差和壳体表面温度随输入转速的变化。实验测试了硅油风扇离合器的滑差和壳体表面温度随输入转速的变化。计算结果和实验值基本一致,证明了模型的正确性。
利用所建立的模型和开发的计算程序,计算分析了另外6款硅油风扇离合器的滑差和壳体表面温度,计算结果和实测结果具有较好的一致性。
本文中提出的计算硅油风扇离合器的滑差和壳体表面温度随输入转速变化模型,可以用于硅油风扇离合器的产品设计开发,在对多方案设计进行优选时,可节省大量的改进设计和实验工作,缩短硅油风扇离合器的开发周期。
[1] Lee Man Hyung, Kim Myoung Kook, Park Hyung Gyu. Electronically Controlled Viscous Cooling Fan Clutch in the Vehicle[J]. International Journal of Precision Engineering and Manufacturing,2011,12(6):983-992.
[2] Lee Kyu Hyun, Lee Joo Heon. Development of a Continuously Variable Speed Viscous Fan Clutch for Engine Cooling System[C]. SAE Paper 980838.
[3] Nikhil Bhat, Sameer Joshi, Ken Shiozaki, et al. Adaptive Control of an Externally Controlled Engine Cooling Fan-drive [C]. SAE Paper 2006-01-1036.
[4] 李惠珍,孙军.硅油风扇离合器传递扭矩计算方法的研究[J].内燃机学报,1989,7(1):45-52.
[5] 王益有.硅油风扇离合器匹配设计的研究[D].广州:华南理工大学,2010.
[6] 姜继海.液体变粘度缝隙流动理论与解析[M].北京:国防工业出版社,2005.
[7] 魏宸官,赵家象.液体粘性传动技术[M].北京:国防工业出版社,1996.
[8] 黄家海,方文敏,邱敏秀.流体黏温特性对液黏调速离合器传动特性的影响[J].上海交通大学学报,2011,45(11):1619-1625.
[9] Huang Jiahai, Wei Jianhua, Qiu Minxiu. Laminar Flow in the Gap Between Two Rotating Parallel Frictional Plates in Hydro-viscous Drive[J]. Chinese Journal of Mechanical Engineering,2012,25(1):144-152.
[10] Huang Jiahai, Fan Yurun, Qiu Minxiu, et al. Effect of Groove on the Behavior of Flow Between Hydro-viscous Drive Plates[J]. Journal of Central South University of Technology,2012,19:347-356.
[11] Huang Jiahai, Qiu Minxiu, Liao Lingling, et al. Numerical Simulation of Flow Field Between Frictional Pairs in Hydro-viscous Drive Surface[J]. Chinese Journal of Mechanical Engineering,2008,21(3):72-75.
Calculation and Measurement of the Slip and Heat DissipationPerformance of Silicone-oil Fan Clutches
Shangguan Wenbin1,2, Song Liming1, He Pinyan2, Duan Yaolong2& Zhu Feifei2
1.SchoolofMechanical&AutomotiveEngineering,SouthChinaUniversityofTechnology,Guangzhou510641;2.XuelongGroupCo.,Ltd.,Ningbo315800
Taking a silicone-oil fan clutch with double grooves as the object of study, with consideration of the viscosity change with shear radius, calculation models for the slip and housing surface temperature of silicone-oil fan clutch are set up, with which the changes in clutch slip and housing surface temperature with input rotation speed are calculated. In addition, a test bench for silicone-oil fan clutch is also built to conduct corresponding measurements. The results of calculation well agree with test data, verifying the correctness of the model built. Finally with the models built, the slip and housing surface temperature of six other silicone-oil fan clutches are calculated and compared with test results.
silicone-oil fan clutch; clutch slip; heat dissipation performance; calculation; measurement
*宁波市2013年度产业技术创新及成果产业化科技专项(2013B10012)和国家自然科学基金(51275175)资助。
原稿收到日期为2013年6月14日,修改稿收到日期为2013年7月31日。
