基于模拟驾驶员多目标决策的汽车自适应巡航控制算法*
2015-04-12高振海李红建胡振程
高振海,严 伟,李红建,胡振程
(1.吉林大学,汽车仿真与控制国家重点实验室,长春 130022; 2.中国第一汽车集团公司技术中心,长春 130011)
2015118
基于模拟驾驶员多目标决策的汽车自适应巡航控制算法*
高振海1,严 伟1,李红建2,胡振程1
(1.吉林大学,汽车仿真与控制国家重点实验室,长春 130022; 2.中国第一汽车集团公司技术中心,长春 130011)
汽车自适应巡航控制系统根据本车与前车之间的相对距离和相对速度,综合考虑车间行驶安全性、本车纵向动力学特性和驾乘人员的舒适性等多个相互关联且存在一定矛盾的性能指标,实现本车与前车安全车间距的保持控制。针对这一多目标协调控制问题,本文在动态输出反馈控制框架下,模拟真实驾驶员对车间距控制的行为特性,利用汽车行驶状态和控制变量建立了安全性、轻便性、舒适性和工效性指标,进而基于不变集和二次有界性理论提出了以上多性能指标的动态协调控制机制,建立了一套自适应巡航控制系统的车间距控制算法。最终通过跟随、驶离和切入3种典型工况的仿真,验证了算法对安全车间距保持和协调多性能指标的可行性和有效性。
自适应巡航;车间距控制;多目标协调;控制约束;二次有界性
前言
汽车自适应巡航控制(adaptive cruise control, ACC)系统在传统定速巡航控制基础上,可以根据本车与前车之间相对运动关系,主动控制汽车纵向速度,以保持本车与前车的安全车间距[1]。伴随着汽车安全技术的发展,ACC已成为国际汽车安全研究领域的焦点。
早期的ACC研究多为在汽车固有的加速和制动等纵向动力学性能基础上确定一个合适的安全车间距,直接根据本车与前车之间的相对距离和相对速度等信息实施距离控制或速度控制[2]。随着研究的深入,研究人员尝试兼顾车与车之间的行驶安全性和驾乘人员舒适性等多个相互关联且存在一定矛盾的性能指标,采用多目标决策技术解决本车与前车安全车间距的保持控制问题[2]。
近年来国际上ACC研究的最新发展趋势和前沿技术是利用模型预测控制(model predictive control, MPC)对多性能指标的协调控制特点,将ACC系统的多目标决策问题转化为多性能指标协调控制。如文献[3]中应用MPC理论建立安全车间距的过渡操作,并设置控制约束和状态约束以满足舒适性和安全性要求。文献[4]中将MPC理论应用于稳态跟随车间距控制算法的设计,协调了燃油经济性、跟踪性能和驾驶员期望响应等性能。但由于MPC算法本身存在计算复杂等问题,每个采样时刻的计算时间可能超过ACC系统的采样时间,导致系统性能恶化;MPC算法也要求模型的外部干扰是可测的(车间相对运动学的外部干扰,即前车加速度一般不可测)。研究人员也提出了一些改进型MPC方法,如文献[5]中在ACC系统决策算法设计中引入显式MPC,通过离线求解优化算法在线查表降低了在线计算时间。
ACC系统研究的出发点是辅助或替代真实驾驶员去实现安全车间距的保持。如何有效利用并模拟真实熟练驾驶员对两车安全间距的控制行为特性,是实现ACC控制且保证控制算法能被乘员广为接受的有效技术途径。
为此,本文中在文献[6]中关于驾驶员速度控制行为研究的基础上,模拟真实驾驶员对汽车安全间距控制以及对行驶安全性、操控便利性、乘坐舒适性和驾驶任务完成的快捷性等多目标协调控制,在动态输出反馈(dynamic output feedback, DOF)控制框架下,利用汽车行驶状态和控制变量建立了安全性、轻便性、舒适性和工效性指标,并基于不变集和二次有界性理论建立了以上多性能指标的动态协调控制机制,将理想纵向加速度的决策转化为带有状态约束和控制约束的系统的镇定问题,实现了保持ACC系统安全车间距的理想控制目标的动态决策。最后通过跟随、驶离和切入等ACC典型行驶工况的性能仿真,验证了算法对安全车间距保持的有效性和协调多性能指标的可行性。
1 问题描述
ACC系统一般包括信息感知层、决策层和控制层,如图1所示。信息感知层获取本车行驶状态信息和前方道路交通环境信息,并确定前方有效跟踪目标车;决策层根据本车与前车的相对距离等信息,确定理想纵向加速度等纵向动力学控制指令;控制层考虑车辆纵向动力学特性(如发动机反拖与制动性能)实现对理想纵向加速度的精确跟踪。本文中着重于解决ACC决策层的理想加速度决策问题。
如上所述,综合考虑车与车之间的行驶安全性、本车纵向动力学特性和驾乘人员舒适性等多个相互关联且存在一定矛盾的性能指标,实现本车与前车安全车间距的保持控制是当前ACC系统研究的核心问题。
针对这一多目标协调控制问题,本文中采用了控制技术中的二次有界性方法[7],面向ACC多目标决策问题,建立了多性能指标的动态协调控制机制,将理想纵向加速度的决策转化为带有状态约束和控制约束的系统的镇定问题。
与MPC算法相比,二次有界性算法存在如下特点。
(1) 实时性更好。MPC算法在线优化过程的计算较复杂,不适合直接应用于像ACC这种对实时性要求高的系统[8]。而二次有界性算法的核心是DOF控制器,其增益是离线设计的,减少了决策算法的在线计算时间,同时该算法也具有与MPC算法相似的协调多性能指标的功能;
(2) 鲁棒性更好。在MPC算法的设计中,假设外部干扰(在ACC系统中外部干扰指前车加速度)是可测的。而在二次有界性算法的设计中,假设外部干扰是有界的,合理地设定外部干扰的界可保证算法较好的抗干扰能力。
鉴于二次有界性方法在处理外部干扰及状态约束和控制约束方面的优势,本文中采用了二次有界性方法,实现ACC中理想纵向加速度决策这一多目标协调控制。
2 车间距控制算法的设计
参照文献[7],本文中首先建立了面向DOF控制器设计的模型—汽车跟随Tanaka-Sugeno(T-S)模糊模型;然后利用汽车行驶状态和控制变量量化多性能指标,将理想加速度的决策转化为带有状态约束和控制约束的T-S模糊模型的镇定问题;最后,利用二次有界性理论设计DOF控制器,将模型状态镇定到由公共Lyapunov矩阵确定的椭球不变集内。
2.1 汽车跟随T-S模糊模型
根据前车与本车的相对距离和相对速度关系及本车的纵向动力学特性,建立汽车跟随模型:
(1)
其中:
x(t)=[ΔdΔvah]T;u(t)=ades;

B1=[0 0 1/T]T;E1=[0 1 0]T

由于式(1)是依赖于速度的非线性系统,不能直接利用现有的线性系统理论中的方法求解该系统的控制律。利用扇形非线性法局部线性化非线性系统可得到T-S模糊模型[11]。T-S模糊模型被认为是逼近非线性系统的万能逼近器。利用线性系统理论中的方法可方便地研究T-S模糊模型。局部线性化式(1)得汽车跟随T-S模糊模型:
(2)
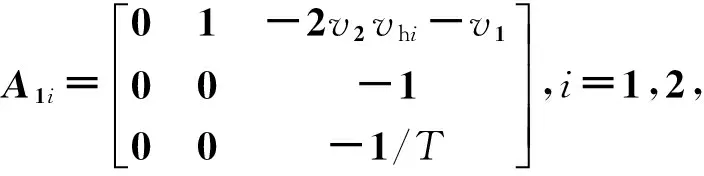
考虑到u(k)=u(k-1)+Δu(k),利用欧拉方法离散化式(2)得
(3)

2.2 多性能指标的量化
参照文献[2]中驾驶员速度控制行为特性的研究,本文中分别建立了安全性、轻便性、舒适性和工效性4个评价指标。
Δd和Δv反映了安全性指标。前车后方理想车间距处是本车的理想跟踪目标点,该点的速度等于前车速度,即Δv=0。Δd和Δv轨迹收敛到理想跟踪目标点附近的邻域内能够保证车辆的安全性。Δd<0且其绝对值越大,相对距离越小,安全性指标越低。因此,约束Δd的绝对值可以保证车辆间的安全性,亦可避免其它车辆频繁切入。
ah和u反映了舒适性指标。ACC系统在保证车辆安全性的情况下主要是一个舒适性系统,因此,在决策算法设计中必须考虑舒适性指标以提高乘员接受性。利用理想加速度表征舒适性指标。较强的加/减速度一方面使乘员感觉不舒适导致系统被弃用,另一方面可能导致电控执行机构饱和甚至损坏。
Δu反映了轻便性指标。Δu表征了加速度变化量或加速/制动踏板的变化量。就通常的汽车驾驶来说,一方面汽车行驶速度等状态量不可能急剧突变;另一方面频繁加/减速给汽车零部件带来机械磨损,缩短了零部件的使用寿命。控制量变化急剧也会导致乘坐舒适性的下降。从驾驶员角度考虑,油门/制动的变化量越小,汽车行驶速度等状态量的改变也越小,轻便性指标越好。
为了协调以上性能指标以综合保证ACC系统性能,本文中首先利用状态约束和控制约束描述了各性能指标的合理取值范围。
其中:
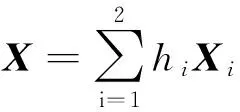
Zi=[0 1 -2v2vhi+v10];
2.3 DOF控制器
如前所述,利用状态和控制变量量化了多性能指标,并以状态约束和控制约束描述了多性能指标的取值范围,将理想加速度的决策问题转化为带有状态约束和控制约束的T-S模糊模型镇定问题。
针对带有状态约束和控制约束的T-S模糊模型的镇定问题,本文中在DOF控制框架下,利用二次有界性理论将状态镇定到由公共Lyapunov矩阵确定的椭球不变集内。
利用并行分布补偿(PDC)技术[11],给出DOF控制器模型为
(4)
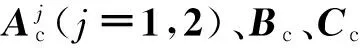
(5)
其中:


如图2所示,状态约束定义了车辆正常驾驶集R。由车辆正常驾驶集内出发的初始状态,取遍控制约束集内所有控制量,在某一时刻能够到达的所有状态的集合,称为车辆可达集。
本文中采用的DOF控制器设计的主要思想是:针对在R内的初始状态,在存在有界外部干扰(前车加速度)情形下,寻找控制律最小化可达集。

通过推导得到了DOF控制器存在的线性矩阵不等式条件及状态约束和控制约束满足的线性矩阵不等式条件。求解线性矩阵不等式组得到DOF控制器模型为
u(k)=Δu(k)+u(k-1),u(0)=0
Δu(k)=10-3×[0.27960.109-0.0024-0.1405]xc(k)+[0.25450.7617-0.324-0.7822]y(k);


3 仿真实验
利用跟随、驶离和切入等ACC系统典型工况的仿真,进一步验证本文中设计的二次有界性算法对安全车间距保持和多性能指标协调的可行性和有效性。仿真中,利用汽车动力学仿真软件CarSim,建立了国内某款乘用车的整车动力学模型及包括雷达传感和有效目标识别等的ACC系统测试仿真平台,并采用Matlab/Simulink软件搭建了ACC系统的车间距控制算法模块和逆纵向动力学模型[13]。
3.1 跟随工况
跟随工况指当同车道前方有行驶车辆,本车退出传统巡航控制,根据本车与前车的相对速度等信息,自动调整本车行驶速度以和前车保持安全车间距的跟随前车行驶工况。为了实现巡航功能,虚拟一辆前车,其速度vc=110km/h。具体工况设为:本车开始以巡航速度行驶,与前车的初始相对距离为150m,前车以90km/h速度匀速行驶,在40s时加速至100km/h,并以此速度匀速行驶。跟随工况仿真结果如图3所示。
由图3(a)和图3(b)可见,在0~10s,本车跟踪虚拟前车,处于巡航模式,10~30s为过渡过程,即建立理想车间距的过程,30~60s为稳态跟随过程。可以看出,在巡航模式中,本车无误差地跟踪巡航速度。本车检测到前车后,进入过渡过程,当车间距达到设定的安全距离时本车松开油门,发动机怠速运转,汽车利用惯性滑行,以降低本车速度,但汽车滑行运动提供的减速度有限,可能减小车间距,对车辆安全性造成威胁,因此须施加一定程度的制动以保证车间安全性,同时也不会对乘员舒适性造成大的影响(见图3(c))。在稳态跟随模式中,本车稳定跟随前车,距离误差和相对速度都约束在设定的范围内,保证了车辆的安全性。
由图3(c)可见,本车加速度在给定的舒适性约束界内。由油门开度和制动压力曲线看出,执行器信号平滑,说明ACC系统满足驾驶轻便性要求。
3.2 驶离工况
驶离工况指本车在跟随前车过程中,在某时刻前车切出或加速离去,本车进入巡航模式的工况。具体工况设为:前车以80km/h速度匀速行驶,在20-30s,前车加速至120km/h,本车初始速度为79km/h,处于稳态跟随模式。驶离工况仿真结果如图4所示。
由图4(a)和图4(b)可见,0~27.5s,本车稳定跟随前车,在27.5s,本车加速到110km/h,进入巡航模式,前车继续加速至120km/h。可以看出,本车由稳态跟随模式切换为巡航模式,其速度无超调,而且在跟随过程中距离误差和相对速度均在设定的安全性约束界内。图4(b)中,在54s左右,前车速度突变为110km/h,这是由于前车驶出雷达测量范围,雷达所测相对速度恢复为默认值0。
由图4(c)可见,本车加速度在给定的约束界内,而且油门曲线无频繁震荡,说明了所设计ACC系统满足舒适性和轻便性要求。
3.3 切入工况
切入工况指本车前方有车辆从相邻车道并入同车道的工况。具体工况设为:本车开始处于巡航模式,速度为110km/h,相邻车道前方300m处一辆以80km/h速度行驶的车辆,在15s时开始向本车所在车道换道,在18s时本车检测到相邻车道的车辆,并且两车间的侧向距离小于设定的阈值,满足所检测到的车辆作为前车的条件,因此本车施加制动,以避免发生碰撞。切入工况仿真结果如图5所示。
由图5(a)和图5(b)可见,0~18s,本车处于巡航模式,在18s时,本车施加制动以建立理想车间距跟随前车,以避免与前车发生碰撞。因此,本车快速减速到80km/h,而且车间距无超调地趋于理想车间距,说明所设计系统对工效性和安全性进行了协调。
在切入工况中,安全性应是评价系统优劣的首要指标。由图5(c)可以看出,本车产生较大的减速度,牺牲了一定程度的乘员舒适性,但是保证了车辆的安全性。
4 结论
本文中模拟真实驾驶员对安全车间距的多目标决策行为,在DOF控制框架下,建立了一个综合协调行驶安全性、操控便利性、乘坐舒适性、驾驶任务完成快捷性等多性能指标的ACC系统理想纵向加速度的二次有界性算法,并进行了跟随、驶离和切入等典型工况仿真分析,研究结论如下。
(1) 利用车间相对运动学模型的状态和控制输入量化了多性能指标,并以状态约束和控制约束描述了多性能指标的界,其中多性能指标的约束界通过分析真实驾驶数据得到,从而体现了真实驾驶员的跟随行为特性。
(2) 利用二次有界性理论能够处理状态约束和控制约束的特点,设计了DOF控制框架下的二次有界性算法,将车间相对运动学模型的状态镇定到包含多性能指标约束确定的集合的椭球不变集内,从理论上保证了安全车间距保持并协调了多性能指标,仿真结果表明了多性能指标在各种典型工况中均处于设定的约束界内,所设计算法有效改善了驾驶员接受性和ACC系统的使用率。
[1] Swaroop D, Rajagopal K R. Intelligent Cruise Control Systems and Traffic Flow Stability[C]. California PATH Research Report. UCB-ITS-PRR-98-36. Dec.1998:1-21.
[2] 管欣,王景武,高振海,等.基于驾驶员行为模拟的ACC控制算法[J].汽车工程,2004,26(2):205-209.
[3] Vibhor L, Bageshwar W L, Rajamani R. Model Predictive Control of Transitional Maneuversfor Adaptive Cruise Control Vehicles[J]. IEEE Trans. Veh. Tech.,2004,53(5):1573-1585.
[4] Li S E, Li K, Wang J. Economy-oriented Vehicle Adaptive Cruise Control with Coordinating Multiple Objectives Function[J]. Vehicle System Dynamics,2013,51(1):1-17.
[5] Naus G J L, Ploeg J, Molengraft V D, et al. Design and Implementation of Parameterized AdaptiveCruise Control: An Explicit Model Predictive Control[J]. Control Engineering Practice,2010,18:882-892.
[6] 王景武.汽车自适应巡航的最优预瞄加速度控制算法研究[D].长春:吉林大学,2004.
[7] Ding B. Quadratic Boundedness via Dynamic Output Feedback forConstrained Nonlinear Systems in Takagi-Sugeno’s Form[J]. Automatica,2009,45(9):2093-2098.
[8] 席裕庚,李德伟,林姝.模型预测控制-现状与挑战[J].自动化学报,2013,39(3):222-236.
[9] Fancher P, Bareket Z, Peng H, et al. Research on Desirable Adaptive Cruise Control Behavior in Traffic Streams[C]. Ann Arbor,MI: University of Michigan Transportation Research Institute (UMTRI),2002, UMTRI-2002-16.
[10] Rajamani R, Shladover S E. An Experimental Comparative Study of Autonomous and Co-operative Vehicle-follower Control Systems[J]. Transportation Research,2001,9C(1):15-31.
[11] Tanaka K, WangH O. Fuzzy Control Systems Design and Analysis[M]. Wiley Inc,New York,2001.
[12] Alessandri A, BagliettoM, Battistelli G. On Estimation Error Boundsfor Receding-horizon Filters Using Quadratic Boundedness[J]. IEEE Trans. Auto. Control,2004,49:1350-1355.
[13] 李朋,魏民祥,侯晓利.自适应巡航控制系统的建模与联合仿真[J].汽车工程,2012,34(7):622-626.
A Vehicle Adaptive Cruise Control Algorithm Based onSimulating Driver’s Multi-objective Decision Making
Gao Zhenhai1, Yan Wei1, Li Hongjian2& Hu Zhencheng1
1.JilinUniversity,StateKeyLaboratoryofAutomobileSimulationandControl,Changchun130022;2.ChinaFAWGroupCorporationR&DCenter,Changchun130011
According to the distance and relative velocity between host vehicle and preceding vehicle, the adaptive cruise control (ACC) system concurrently considers three correlated and contradictory performance indicators of driving safety between vehicles, longitudinal dynamics characteristics and the comfort performance of driver and occupants to achieve the control for maintaining safe inter-vehicle distance. Aiming at this multi-objective coordinated control problem, the behavior characteristics of real driver in inter-vehicle distance control are simulated under the framework of dynamic output feedback control and four indicators of safety, handiness, comfort and efficiency are set up based on the driving state and control variables of vehicle. Then a dynamic coordinated control mechanism for above-mentioned performance indicators is proposed based on invariant set and quadratic boundedness theory and a set of inter-vehicle distance control algorithms for ACC system are worked out. Finally simulations on three typical operation conditions (following and the cut-out and cut-in of preceding vehicle) are conducted to verify the feasibility and effectiveness of the proposed algorithms in safe inter-vehicle distance maintenance and multi-performance indicators coordination.
ACC; inter-vehicle distance control; multi-objective coordination; control constraint; quadratic boundedness
*国家自然科学基金(50975120)、973计划前期研究专项(2012CB723802)和长江学者和创新团队发展计划(IRT1017)资助。
原稿收到日期为2013年7月18日,修改稿收到日期为2013年10月4日。
