纯电动汽车动力锂电池Nernst模型参数辨识*
2015-04-12康燕琼
毕 军,康燕琼,邵 赛
(北京交通大学,城市交通复杂系统理论与技术教育部重点实验室,北京 100044)
2015127
纯电动汽车动力锂电池Nernst模型参数辨识*
毕 军,康燕琼,邵 赛
(北京交通大学,城市交通复杂系统理论与技术教育部重点实验室,北京 100044)
建立了电动汽车动力锂电池的Nernst经验模型,并利用遗忘因子递推最小二乘法对模型参数进行辨识。以北京市运营的纯电动环卫车的锂电池数据对所建立的模型和参数辨识算法进行验证,结果表明,所给出的方案是有效的,具有算法运算量少、模型结构简单和辨识精度较高等优点,适于电动汽车运行时对电池模型参数的在线辨识。
电动汽车;电池模型;参数辨识;最小二乘法
前言
电池作为一种储能设备,其可靠性、稳定性和安全性已经逐渐成为电动汽车潜在消费者最关注的问题。电池中的电解液本身具有挥发性和易燃性,且易与所处外界环境发生热交换。为此,除了提高电池技术,还有必要建立一套完整的电池管理系统(BMS),用以实时监测电池组的性能参数,如总电流、总电压等。精确估计电池SOC值是BMS最重要的任务[1-2]。电池的SOC值无法直接测得,只能根据电池的电压、电流、温度和内阻等参数估计得到,即建立合理的电池模型。目前所研究的电池模型主要有等效电路模型、神经网络模型和经验公式模型等[3]。等效电路模型是应用比较直观的电阻、电容、电感等电路元件来描述电池的非线性特性,如Thevenin模型、四阶动态模型、PNGV模型等[4-6],但这类电池模型的相关参数不能通过采集的实时数据得到,只能通过实验室的仿真平台求得,这导致模型的实时性和精确性下降。神经网络模型具有非线性、多输入多输出和泛化能力强等优点,其学习能力和并行机构,对于外部激励能给出相应的输出,故能较好地模拟电池的动态特性[7]。目前广泛使用的神经网络方法有BP神经网络与RBF神经网络。RBF神经网络因具有泛化能力强、收敛性好和学习速度快等优点,在电池模型建模中更具优势[8]。神经网络电池模型建模时,一般用电池的电流、电压、温度和上一时刻的SOC值作为输入变量,当前的SOC值作为输出变量,但是该种电池模型对动力电池没有一个具体的数学表达式,不利于分析电池各个性能参数对电池总体性能的影响。经验公式模型是研究人员根据实践经验将电池的特性用一个带有参数的数学表达式来描述,目前广泛应用的经验公式模型有Shepherd模型、Unnewehr Universal模型和Nernst模型[9]等。经验模型具有阶数低,结构简单,利于工程实现等优点,且模型中的参数可利用实时采集到的电池数据辨识得到,既克服了等效电路模型的缺点,相对神经网络模型而言又有比较具体的数学表达式,因此,本文中选用经验公式模型作为锂离子电池模型,应用实时运营的北京市纯电动汽车数据对电池模型的参数进行在线辨识,最后对模型和参数辨识的准确性进行验证。
1 电动汽车运营数据的获取、分析与处理
1.1 数据来源
北京市实时运营的纯电动汽车有环卫车(2t、8t和16t)、出租车和公交车等类型,为确保电动汽车安全、可靠地运行,有必要对电动汽车运营时的电池状态进行远程监控。安装在电动汽车内的车载终端设备利用GPRS无线通信技术,将采集的各种电池数据,周期性地无线发送到电动汽车运营监控中心。电动汽车运行时大量的电池数据都存储在监控中心的数据库服务器中,为论文的实证研究提供了数据支持。由于在所有运行的电动车辆类型中,2t环卫车的数量多,运行时间长,并且数据稳定,因此本文数据来自2t环卫车。2t环卫车电池箱的组成为两箱串联,每箱由60个磷酸铁锂单体电池组成,车辆运行过程中采集到的数据信息类型主要有时间、终端号(车号)、总电压、总电流、SOC值、温度、单体电压、电池箱温度、最高及最低温度、最高及最低单体电压值、报警信息和车辆GPS数据(经度、纬度、速率和方向)等。本文中用到的数据类型有时间间隔、总电流和总电压等。
1.2 数据分析
2t环卫车的原始数据量庞大,提取2号电动环卫车在2012年9月4日-18日的数据进行进一步的分析。图1显示的是这个时间段内2号车SOC的变化情况。由图可知,9月4日、5日两天2号车处于运行状态,因为SOC值整体上呈现下降趋势,但在此过程中,有部分数据的SOC值为0,属于异常数据,这些异常数据使得电动车的放电过程不连续;9月6日电动车处于充电状态,SOC值呈上升趋势,而且整个充电过程连续性很好,数据量大,9月7日采集到的数据均为异常数据(其部分数据如图2所示);9月9日-18日电动车整体处于放电状态,但从图中线1可以看出该放电过程连续性也较差。2号电动车在9月8日、10日、11日、13日、15日、16日、17日没有采集到数据,电动车处于静止状态。综上所述,较放电过程,电池在充电过程中得到的数据连续性好、数据异常情况少,且数据量大,因此使用充电过程的数据作为本文研究的基础数据。提取2号车在9月6日08:01:59-12:24:20的数据并用Matlab对该段充电过程进行绘图,得到该段充电过程中电池总电压、充电电流和电池SOC的变化曲线,如图3和图4所示。
由图可见,在纯电动汽车充电过程中,充电电流相对平稳;电池的SOC值平稳增加,且随着时间的增长呈线性增长趋势;电池的总电压在整个过程中也逐渐上升,但上升的幅度有波动,在整个过程中没有呈现出明显的线性变化趋势。
1.3 数据处理
电动汽车在连续的充电过程中没有出现异常数据,故无须进行异常数据的处理。但根据理论知识,电动汽车在连续充电过程中,电池组的SOC值随着充电时间的增长而增长,但测量仪器的精度为0.4,在实际采集数据的过程中,当数据变化小于0.4时,这种微小变化不会被检测出来,因此使SOC值在一段时间内没有变化(图5),因此仍须对充电数据进行插值处理,使数据更接近电动汽车的实际情况,本文中采用样条插值法[10],具体步骤如下所述。
(1) 从生成的电池数据表中按时间顺序提取电动汽车某一天的连续充电数据,相邻两组数据的时间间隔均为10s,记为X0=[x1,x2,x3,x4,…,xn](n=1 000),n为样本数,xi=[v-total,i-total,soc]。
(2) 遍历X0中的所有数据,在SOC值相同的每组xi中,提取i最小的xi。
(3) 将提取出来的xi按i从小到大的顺序依次排列,方便利用Matlab进行插值处理。
(4) 利用Matlab编程对步骤3中的xi序列进行样条插值,时间间隔仍为10s,插值之后的数据样本数仍为1 000。
2 电池模型的建立和参数辨识
2.1 电池模型的建立
3种经验模型分别为
Shepherd模型:
yk=E0-Rik-k1/xk
(1)
Unnewehr Universal模型:
yk=E0-Rik-k1xk
(2)
Nernst模型:
yk=E0-Rik+k1ln(xk)+k2ln(1-xk)
(3)
式中:yk为k时刻的电池端电压;E0为电池SOC为100%时的电动势;xk为k时刻的SOC值;ik为k时刻的电流;R为电池内阻;k1、k2为模型匹配系数。
上述3个公式中,式(1)和式(2)的非线性程度低,需要辨识的参数少;而式(3)非线性程度相对较高,需识别的参数也较多,更能体现电池系统的复杂性。因此,本文中采用Nernst模型进行辨识,只要得到N组电池数据{yk,ik,xk},即可用下面的遗忘因子递推最小二乘法辨识得到模型的参数。
2.2 模型参数辨识
系统辨识就是在对辨识系统进行输入、输出观测而获得其输入、输出数据的基础上,从一组设定的模型类中,确定一个与被辨识系统等价的数学模型。系统辨识的基本原理如图6所示。
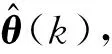
(4)
同时计算出预报误差
(5)
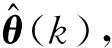
2.2.1 遗忘因子递推最小二乘法参数辨识
最小二乘法通过求解误差平方的最小值寻找数据的最佳匹配函数。该方法不仅可用于在线估计,也可用于离线估计。在随机环境下使用最小二乘法时,无须获得关于观测数据概率统计方面的信息,但得出的结果却具有很好的统计特性,因此被广泛应用于辨识领域,特别是其改进算法,如递推增广最小二乘法、遗忘因子递推最小二乘法等。
电动汽车在充电过程中,SOC值会随时间的累积缓慢增长,因此它是一个慢时变参数。针对慢时变参数,随着数据的增长,如果不考虑历史数据的权重,那么新的观测值对参数估计的修正能力将逐渐减弱。为了克服这个问题,本文中的参数辨识采用遗忘因子递推最小二乘法。
遗忘因子递推最小二乘法解决了在迭代过程中出现的“数据饱和”现象,提高了参数估计的准确性。遗忘因子递推最小二乘法的参数估计的公式为
(6)
(7)
(8)
式中:K(k)为增益矩阵;遗忘因子λ须选择接近1的正数,通常不小于0.9。P(k)为协方差矩阵。
2.2.2 模型参数的辨识步骤

采集7号电动环卫车在2012年9月21日8:10-11:35的充电数据进行参数辨识,此次充电过程大约持续3h,充电数据经过筛选和样条插值之后间隔为10s,样本数为1 000。
具体步骤如下所述。

(2) 采样当前输入输出值yk、ik、xk,确定φ(k)。

3 参数辨识实验与结果分析
初始输入数据7号电动环卫车在2012年9月21日8:10-11:35的充电数据。遗忘因子递推最小二乘法初始参数设置参见2.2.2节,参数辨识的结果如图7所示。
从图7的参数辨识结果图可以得到,参数k0、k1、k2辨识曲线有相似之处,都是在迭代500次之后趋于稳定,最后直到基本收敛。参数R在迭代500次之后仍有较大波动,但最后也基本收敛。表1是辨识得到的各个参数的最终值。
由辨识结果可以得到Nernst经验模型的数学表达式为yk=412.6743-0.2118ik+21.4158ln(xk)+1.9183ln(1-xk)
(9)
根据参数辨识得到的Nernst经验模型的数学表达式,可以进一步验证模型和辨识结果的准确性。取7号电动环卫车在2012年10月1日07:49:24-10:28:25的850条充电数据代入式(9)进行模型验证,评价指标为式(10)所示的相对误差(RE)、式(11)所示的均方根相对误差(RMSRE)。验证结果如图8、图9和表2所示。
(10)

(11)
由图8可见,总电压预测值增长的趋势和真实值基本保持一致,总电压的绝对误差值范围是[0.88,2.87],在误差允许范围内;由图9可见,总电压的相对误差最大值为0.007;表2中RMSRE值为0.005 2。数据表明,Nernst模型参数辨识结果准确。

表2 模型验证结果
4 结论
本文中采用遗忘因子递推最小二乘法对Nernst模型中的参数进行辨识。结果表明,每个参数最后均收敛到一个稳定值,说明辨识方法合理。在进一步的模型验证实验中,Nernst经验模型得到的电压值和真实电压值非常接近,说明该模型简洁有效,相对误差和均方根相对误差的值均小于0.01,进一步表明参数辨识的准确性。此外,本文中在对SOC值的数据处理过程中,只选用了样条插值,没有对比其他数据处理方法,在今后的研究中,宜用多种数据处理方法处理SOC值,寻找最符合SOC值增长规律的方法,进一步提高模型参数辨识结果的准确程度。
[1] He Hongwen, Zhang Xiaowei, et al. Online Model-based Estimate of State-of-charge and Open-circuit Voltage of Lithium-ion Batteries in Electric Vehicles[J]. Energy,2012,39:310-318.
[2] Tsang K M, Sun L, Chan W L. Identification and Modelling of Lithium Ion Battery[J]. Energy Conversion and Management 2010,51:2857-2862.
[3] Hu Xiaosong, Li Shengbo, et al. A Comparative Study of Equivalent Circuit Models for Li-ion Batteries[J]. Power Sources,2012,198:359-367.
[4] Hu Xiaosong, Li Shengbo, et al. Robustness Analysis of State-of-charge Estimation Methods for Two Types of Li-ion Batteries[J]. Power Sources,2012,217:209-219.
[5] Krishnan S Hariharan, Kumar V Senthil. A Nonlinear Equivalent Circuit Model for Lithium Ioncells[J]. Power Sources,2013,222:210-217.
[6] Xiong Rui, He Hongwen, et al. Modeling for Lithium-Ion Batery Used in Electric Vehicles[J]. Procedia Engineering,2011,15:2869-2874.
[7] Yuan Shifei, Wu Hongjie, Yin Chengliang. State of Charge Estimation Using the Extended Kalman Filter for Battery Management Systems Based on the ARX Battery Model[J]. Energies,2013,6:444-470.
[8] Rolando J Praga-Alejo, David S Gonzalez, et al. Statistical Inference in a Redesigned Radial Basis Function Neural Network[J]. Engineering Applications of Artificial Intelligence,2013,26:1881-1891.
[9] Gregory L Plett. Extended Kalman Filtering for Battery Management Systems of LiPB-based HEV Battery Packs[J].Power Sources,2004,134:252-292.
[10] Sarfraz M, Hussain, et al. Modeling Rational Spline for Visualization of Shaped Data[J]. Journal of Numerical Mathematics,2013,12:63-67.
[11] Wang Dongqing, Ding Feng, et al. Data Filtering Based Least Squares Algorithms for Multivariable CARAR-like Systems[J]. International Journal of Control, Automation and Systems,2013,11:711-717.
[12] Chen Ting, Braga Neto U M. Maximum-Likelihood Estimation of the Discrete Coicient of Determination in Stochastic Boolean Systems[J]. IEEE Transactions on Signal Processing,2013,61:3880-3894.
[13] Garrida J, Vazquez F, et al. Centralized Multivariable Control by Simplified Decoupling[J]. Journal of Process Control,2012,22:1044-1062.
[14] 庞中华,崔红.系统辨识与自适应控制MATLAB仿真[M].北京:北京航空航天大学出版社,2009.
Parameters Identification of Nernst Model for PowerLithium-ion Battery of Pure Electric Vehicles
Bi Jun, Kang Yanqiong & Shao Sai
BeijingJiaotongUniversity,MOEKeyLaboratoryforUrbanTransportationComplexSystemsTheoryandTechnology,Beijing100044
A Nernst empirical model for the traction lithium-ion battery of electric vehicle is established, and the recursive least square algorithm with forgetting factors is adopted to identify model parameters. The model established and the parameter identification algorithm adopted are verified by using the lithium-ion battery data of refuse collecting electric vehicles operating in Beijing city. The results indicate that the scheme has advantages of less computation efforts, simple model and high identification accuracy, and is effective and suitable for online parameter identification of battery model in electric vehicle operation.
electric vehicle; battery model; parameter identification; least square method
*中央高校基本科研业务费专项资金(2013JBM)和北京市科技计划项目(Z111109073511001)资助。
原稿收到日期为2013年10月14日,修改稿收到日期为2013年12月30日。
