矿井井架起吊受力有限元分析
2015-04-10邢启风
邢启风
(唐山开滦建设(集团)有限责任公司,河北 唐山 063000)
矿井井架起吊受力有限元分析
邢启风
(唐山开滦建设(集团)有限责任公司,河北 唐山 063000)
针对大型矿井井架钢结构起吊过程中关键点的受力变化问题,利用有限元分析获取了井架起吊受力的大量运算数据,得出细致准确的井架吊装工程中的力学变化结论,同时也为同类吊装工艺提供更为科学的参考依据。
矿井井架;起吊;有限元分析;数据
1 井架结构的有限元分析
在井架的施工过程中,会出现诸如应力场和位移场等工程实际问题。而对于这些问题的分析计算,以前往往是通过给定约束简单限制前提下,利用偏微分方程解决这些问题。这种求解的方法适应范围很窄,对较简单且几何边界规则的问题还可以,对较复杂的问题却很难完成。为了能利用力学公式计算,需要去简化问题:如过度简化问题,得到的结论有时是不正确的解;对于复杂井架结构来说,利用偏微分方程解决现实复杂的受力问题,很难完成求解。
在实际的工程运用当中,如井架的形状、外观、起吊施工方法等各方面的约束,使得井架的力学特征呈非线性关系,相对比较复杂,简化起来利用力学公式计算也更为困难;为解决这方面的问题,运用力学理论与现代数学相结合的方法,充分发挥计算机工具的优势,来获得井架受力的数值解。
井架的有限元方法分析步骤:
1)确定井架计算模型。对井架采取离散结构,进行网格划分。将井架进行总体剖分,将其划分为有限个结构单元,组成的每个结构单元上设有8个节点;相邻的各单元间,通过节点连为一体,让这些人为划分的结构单元的结合体,去替代原来较复杂的井架结构。
2)对井架单元分析。先假定井架单元位移函数,使之形成节点间力和位移的函数关系;通过单元刚度矩阵使它把外载荷转化成单元节点上的载荷,从而实现力的变换。
3)为了能用节点位移表示井架任意单元内的任何一点处的应力应变值,引入位移函数,使之建立起位移与坐标的某种关系。
4)运用弹性力学的几何方程,形成井架弹性单元节点位移与单元应变的关系,从而分析井架弹性单元的力学特性。
5)划分的井架单元的等效节点的连续弹性体在离散化后,可实现从一个单元到相邻单元的力的传递。这样就把单元上的集中力、体积力和表面力等效到单元的各节点上,形成等效的节点载荷。
6)井架单元的整体分析。对井架单元的刚度矩阵进行总体集中,形成井架总刚度矩阵,这样井架单元节点平衡方程就汇总成了井架结构的整体方程组。
7)进行边界条件处理。通过井架位移的边界条件,去除井架总体刚度矩阵的特异部分,把井架的整体的平衡方程完善。
8)求井架结构平衡方程。井架结构的平衡方程是以总刚度矩阵为稀疏的线性代数方程组,解此方程组可得到井架单元节点的位移分量。
9)计算井架单元应力。解出的单元各节点位移的分量,汇总可得到单元的应力值。
根据以上步骤不断对优化的网格参数进行运算,可得到井架对外载荷作用下各部位的应力、应变和位移的数值。
2 建立井架三维实体模型
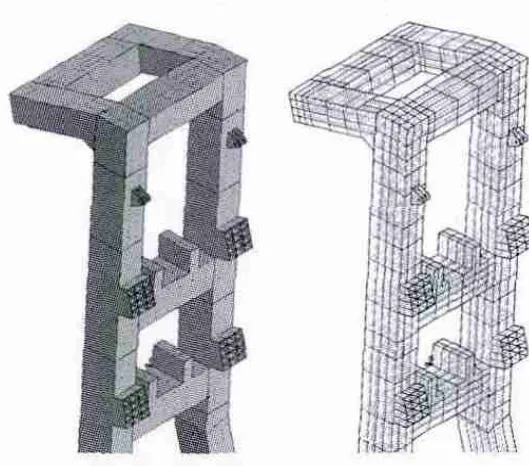
图1 斜撑上局部结构
为保证分析计算的正确性和精确性,工程应用了美国著名的UGS公司的三维设计软件,严格按照井架的工程图纸中的几何及尺寸参数完成了井架三维实体建模,如图1~图4所示。该模型是以淮南矿业集团丁集煤矿主井井架为参数建立的模型;该井架为对面双提升亭式井架、井架的起重架上平面标高为+69.000 m;A、B两个斜撑设计完全相同,两斜撑的底部中心线距离为32840.4 mm,每个斜撑的根部距离为36988.6 mm。井架斜撑沿提升线方向,为变截面,每个斜撑两柱上端中心线宽为8600 mm,斜撑变截面点处的标高+48.000 m,安装完毕后两斜撑合拢呈“A”字形状。井架设计净重800.88t;井架与基础的连接为T型螺栓铰接;结构钢材料为Q235-C,密度是7.85 g/cm3,起吊单件斜撑最大质量331908.2 kg,质心距井架底部距离为40725.3 mm。
3 井架有限元分析
3.1 井架三维模型的导入

图2 斜撑中局部结构

图3 斜撑下局部结构

图4 斜撑铰链支座结构
用三维设计软件的优异建模功能建立的井架三维实体模型,通过.sat文件格式转换后导入ANSYS软件前处理模块环境。
3.2 井架三维模型有限元单元选择与材料参数
1)单元划分。首先是选定具有二次方位移的solid 45单元,划分的单元由8个节点来进行定义,每个节点有x、y、z三个方向位移的自由度。使划分的单元具有大变形、大张力、蠕动、膨胀、可塑性和应力刚化的能力。采用手动划分网格,以每条线300的尺寸划分,共得到350509个单元。
2)材料参数。材料选用弹性模量为2.1×105MPa,泊松比为0.3,其密度是7.85 g/cm3。
3.3 井架载荷及边界条件
起吊井架斜撑的载荷及受力分析,需考虑的是约束和加载两方面问题。
约束与加载:在整个井架起吊过程中铰链底座是固定不动的,所以将铰链底座的底面约束其全部自由度。根据起吊到不同角度时,起吊力与斜撑的夹角变化进行力F的加载,同时再对斜撑施加竖直向下的重力加速度g,如图5所示,在图中显示了力分析中的加载,约束以及重力之间的相互位置。图6为底部支撑铰链约束位置放大图。
3.4 井架有限元运算结果与分析

图5 加载示意图
为使井架起吊安全,需通过有限元分析来充分了解井架起吊的几个关键受力点,它包括井架在起吊时,最大构件(斜撑)起吊时的最大应力,通过铰链反转实现井架起吊的底座铰链销轴的最大应力,底座铰链上部承受的最大应力和井架整体变形位移等问题。
1)起吊过程的斜撑最大应力。
图7~图9显示了井架在不同起吊角度下井架以及铰链的等效应力云图,在图中不同的颜色代表了不同应力值,其值与下面的颜色条中的值相对应;以下图片为截取的0°~80°等不同角度中斜撑最大受力值图。
从表1应力云图汇总表中可以看出,起吊到10°时,最大应力为215.681 MPa,其他角度的应力都小于这个值,且最大应力值仍小于所选材料Q235-C钢的屈服极限,井架及铰链在起吊过程中是安全的,不会发生屈服变形。

图6 底部支撑铰链约束

图7 起吊斜撑10°时左视应力云图

图9 起吊斜撑10°时最大应力处局部

表1 起吊过程的斜撑(在铰链处)最大应力
2)底座铰链销轴的应力有限元分析。
图10~图12为截取的0°~80°等不同角度中最大受力值图。

图10 井架斜撑50°时销轴的剪切应力云图
表2是铰链的销轴在不同的起吊角度下,利用有限元软件得出的销轴的剪切应力。

表2 销轴在不同角度下的剪切应力
从上面的图和表中,可以看出销轴的最大剪切应力一直在90 MPa以内,对于最大剪切应力117.6 MPa的Q235-C能满足强度要求。但从表2中可以得出,随起吊角度的增大,剪切应力在50°达到最大,而后逐渐减小。
3)底座铰链上部的应力有限元分析。
铰链上部与井架箱体焊接部位的焊缝的受力变化,其应力如表3所示,铰链上支座的应力云图如图11所示。

图11 井架斜撑40°时上支座应力云图
图中图片为截取的0°~80°等不同角度中最大受力值图。表3为焊接部位的应力随起吊角度的变化。

表3 铰链上部与井架箱体焊接部位的应力变化MPa
小结:从此表中可以得出,在0°~80°随起吊角度的增大,焊缝的应力值在40°时最大,也未超过选用材料Q235-B所允许的强度要求。
4)井架整体的变形位移分析。
通过有限元分析计算,得出井架整体的变形位移随起吊角度的变化情况,起吊斜撑70°时井架变形位移量最大。图12为截取的显示井架在不同起吊角度下井架以及铰链的变形位移值最大395.6 mm的图。
4 井架起吊的有限元分析结论
通过对井架起吊过程的有限元分析得出以下结论:
1)井架斜撑在起吊过程中,10°的位置应力值达到最大;此时对于销轴,其最大应力点在销轴下部偏向销轴受挤压部位,位置和力学的理论计算相符。
2)井架斜撑10°时销轴的最大剪切应力为销轴靠中间位置;20°~80°时销轴的最大剪切应力为销轴边缘位置;随着起吊角度的增大,剪切应力在40°~50°达到最大,而后逐渐减小。

图12 起吊斜撑70°时井架变形位移
3)对于铰链上部与井架箱体焊接部位的焊缝的受力变化,有限元分析的结论是:在0°~80°随起吊角度的增大焊缝的应力值在40°~50°范围时最大,峰值出现在40°位置。
4)通过有限元分析计算,得出井架整体的变形位移随起吊角度的变化情况,起吊斜撑70°时井架变形位移量最大。
井架起吊现场图片如图13所示。
5 结语
通过对井架支撑结构吊装过程的有限元分析,得到大量的数据和可视化图形。全面、清晰的应力场、变形位移场,为评价大型井架支撑结构的设计和吊装过程中的安全合理性提供了可靠的依据,减小了过去采用材料力学和理论力学验算强度及安全系数的误差,发现了可能出现的薄弱环节和问题,并及时采取有效的措施。

图13 两斜撑合拢图片
[1]中华人民共和国建设部,中华人民共和国国家质量监督检验检疫总局.钢结构设计规范:GB50017-2003[S].
[2]杨文渊.起重吊装常用数据手册[M].北京:人民交通出版社,2001.
(编辑 明 涛)
TD541
A
1002-2333(2015)08-0096-04
邢启风(1966—),男,工程硕士,高级工程师,从事机电设备的安装与运用研究工作。
2015-02-25
