电力系统扩展黑启动方案的后效性研究

顾雪平 王大江 李少岩 李文云 朱 涛 赵 川

电力系统扩展黑启动方案的后效性研究

顾雪平1王大江1李少岩1李文云2朱 涛2赵 川2

（1. 华北电力大学新能源电力系统国家重点实验室 保定 071003 2. 云南电力调度控制中心 昆明 650011）

大停电后恢复初期阶段的扩展黑启动策略为恢复控制提供了新的思路，针对扩展黑启动方案的后效性研究，将后续网架重构过程离散为次序进行的多个时步，建立了计及后续重构过程中机组启动与负荷恢复交替与协调的多目标网架重构优化模型。结合采用分层序列法、改进细菌觅食算法和最短路径法，从网架重构整体最优的角度求解每一时步的待恢复机组、负荷及相应的恢复路径，进而得到网架重构最优方案；在此基础上，建立了反映重构过程多输入多输出要素的指标集，以超效率数据包络分析模型评估后续网架重构的相对效率，以此效率表征扩展黑启动方案的后效性。基于新英格兰10机 39节点系统的扩展黑启动方案算例分析验证了本文方法的有效性与正确性。

扩展黑启动 后效性 数据包络分析 网架重构 多目标优化

1 引言

电力系统恢复控制研究对优化大停电后的系统恢复措施、减小停电带来的经济和社会损失具有重要意义。近年来，智能电网的建设对提高电网供电可靠性发挥了重要作用[1]，但是随着大规模新能源发电系统的接入，电网的动态特性更加复杂，在各种外部因素的影响下，大停电事故仍然是当前电网运行面临的严重威胁[2]，近期发生的多起大停电事故及恢复过程再次表明研究大停电事故及其恢复控制措施的重要性[3-4]。

大停电后的系统恢复是一个复杂的连续动态过程，通常可分为黑启动、网架重构和负荷恢复三个阶段。黑启动阶段是恢复的初始阶段，是后续恢复的基础。文献[5-7]给出了黑启动方案制定的系统框架；文献[8-10]对黑启动阶段的相关技术问题进行了仿真分析；文献[11-14]研究了黑启动方案评估优选问题；文献[15]提出了以黑启动电源同时启动多个被启动机组的扩展黑启动策略。网架重构是在黑启动阶段建立的局部网络基础上尽快恢复失电厂站并建立稳定的目标网架，在恢复中起着承上启下的作用，是系统恢复研究的关键问题，文献[16-17]从复杂网络理论角度优化目标网架；文献[18-20]侧重从送电路径寻优的角度优化网络重构；文献[21]研究系统从树状网络恢复到环状网络时的优化算法；文献[22]建立了分布式恢复的主从递阶决策模型；文献[23-25]分别提出了不同的多目标网架重构模型方法。上述研究成果从不同角度为网架重构做出重要贡献，但是现有的多数研究工作都将黑启动阶段和网架重构阶段分开进行相对独立的研究，而恢复过程是一个连续的动态过程，各个阶段紧密联系，作为后续网架重构基础和前提的黑启动阶段，其恢复效果直接影响后续的重构过程。

扩展黑启动策略同时启动多台机组形成局部小网络，完成了部分网架重构过程，不仅拓展了黑启动阶段的恢复范围，更有利于加快后续网架重构进程。不同的扩展黑启动方案恢复形成的小网络包含的机组数目及特性不同，已恢复节点和线路的拓扑位置不完全相同，对系统后续恢复的效果产生不同的影响。因此有必要研究扩展黑启动方案的后效性，综合效果优的方案不仅黑启动阶段恢复效果好，还应有利于后续的网架重构，可为黑启动阶段恢复方案的综合决策提供重要依据。

本文研究扩展黑启动方案的后效性评价，首先将重构过程离散为多个顺序执行的时步，建立了兼顾机组恢复和负荷恢复的多目标网架重构模型，采用总体协调的分时步重构策略与分层序列法得到每一时步的最优恢复机组、负荷及相应的恢复路径。在此基础上构建了能够全面系统反映网架重构多输入多输出要素的指标集，以超效率数据包络分析模型评估得到的网架重构相对效率来代表扩展黑启动方案的后效性。

2 后续网架重构多目标优化模型

2.1 分时步决策与总体协调的网架重构思路

文献[24]提出了一种分时步决策和总体协调的网架重构思路，本文基于该思路建立扩展黑启动后续网架重构的优化模型。在扩展黑启动策略后续网架重构阶段，已启动的多台机组能够提供较大的功率，具备同时恢复机组及部分重要负荷的能力，机组的启动可以加快重构过程和负荷恢复，适量的负荷投入也有助于保持已恢复系统的稳定，因此网架重构过程是机组恢复和负荷恢复相互影响的交替协调恢复过程，重构目标是构建由机组、枢纽节点和重要负荷组成的骨架网络。重构过程的决策是一个复杂的组合优化问题，若将连续时间过程转化为多个次序执行的离散时步，可大大降低建模复杂度。离散后的重构过程可用图1来说明，其中S0为网架重构的初始状态，对应于黑启动阶段形成的局部网络，{D1,D2,…,DN}为各时步的恢复决策，{S1,S2,…,SN}表示各个时步的目标网架，SN为重构完毕最终目标网架，依据动态规划的基本原理，对离散后每一时步恢复决策从重构全过程最优角度优化，每一时步以一个短期目标网络为恢复目标，以本时步恢复决策中机组、负荷得到启动功率为结束标志及下一时步的开始时刻，根据前一时步的状态及本时步恢复决策递推得到下一时步网络状态从而完成网架重构，求出整个过程的最优决策序列集合，使整个重构过程最优。

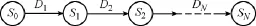
图1 分时步网架重构过程Fig.1 Process of multiple discrete time-step network reconstruction

对后续网架重构采用总体协调的分时步重构策略优化，设时步步长为Δt，Δt取值应适宜，太短则系统增发功率较少，不足以恢复更多机组、负荷，太长则机组、负荷不能尽早恢复，本文取Δt=0.25h。由于不同机组、负荷恢复路径中线路倒闸操作需要耗费时间，本文假设路径中不同线路采用并行恢复方式，待恢复机组和负荷均可在时步末期获得启动功率。

2.2 目标函数

为通用性起见，研究(n-1)Δt～nΔt时间段内的网架重构，由于机组和重要负荷交替协调恢复，将网架重构问题建模为多目标优化模型，针对机组恢复和重要负荷恢复及路径恢复的不同特点分别建立其优化目标函数，进而构建该时段内网架重构整体的多目标优化模型。在得到重构过程各时段通用模型后，逐步优化每一时步的恢复决策而最终完成网架重构。

（1）机组恢复目标。对于在本时步恢复的机组，综合考虑机组特性及所处网络拓扑位置等因素，以其启动后在整个网架重构过程的加权发电量最大为目标，目标函数为

式中，NG为系统中待启动机组的个数；nΔt为第 n个时步结束时刻；T1为优化总时间；Gi(i=1,…,NG)为待启动的第 i台机组；ci为二元决策变量，机组Gi在本时步投入取1，否为0；αGi为Gi所在节点的重要度，以节点收缩后的网络凝聚度表示[17]；PGi(t)为Gi在t时刻的功率，由其特征参数决定，可通过简化的出力曲线获取[24]。

（2）负荷恢复目标。设每个负荷节点的负荷均包含Ⅰ、Ⅱ、Ⅲ三类负荷，Ⅰ类负荷比例为 10%～20%，Ⅱ类负荷比例为 25%～45%，其余为Ⅲ类负荷，负荷恢复优化以恢复的加权负荷量最大为目标，即

式中，NL为系统中负荷节点的个数；μⅠ、μⅡ、μⅢ为Ⅰ、Ⅱ、Ⅲ类负荷之间的重要性比例系数，取可使负荷恢复时，优先恢复Ⅰ类负荷，再恢复Ⅱ、Ⅲ类负荷；γj为负荷节点 j(j=1,2,…,NL)中负荷的综合权重，考虑其可靠性、重要性及所在节点重要度等因素，由层次分析法确定；决策变量 cⅠ,j、cⅡ,j、cⅢ,j表示负荷节点 j中I、Ⅱ、Ⅲ类负荷是否在本时步投入，是为1，否为0；PLⅠ,j、PLⅡ,j、PLⅢ,j为节点 j中I、Ⅱ、Ⅲ类负荷的有功功率。

（3）路径恢复目标。机组、负荷恢复时的恢复路径优化综合考虑线路电压等级变化的影响、充电无功和线路的拓扑重要性等因素，以寻找代价最小的包含关键线路的路径为目标，目标函数为

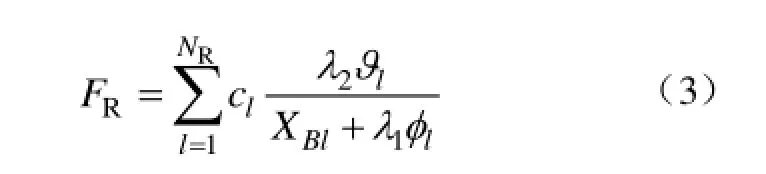
式中，NR为系统中线路数；决策变量 cl表示线路 l是否在本时步投入，是为 1，否为 0；XBl为线路 l的电纳；φl为线路l是否经过电压等级变换，是为1，否为0；转换系数λ1、λ2取 0.5；为线路l归一化后的介数[17]。

在分别定义了机组恢复、负荷恢复及路径恢复的目标函数后，扩展黑启动后续的网架重构可建模为如下的多目标优化模型

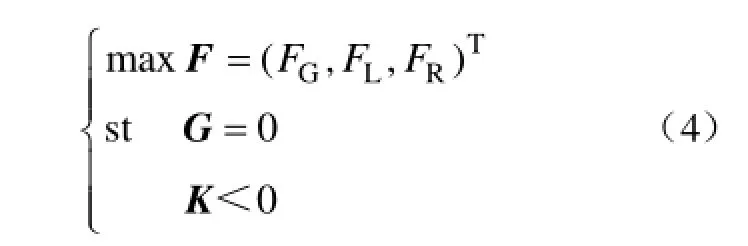
式中，F为目标函数向量；G为等式约束条件；K为不等式约束条件。

2.3 约束条件集

（1）机组启动时间约束。热启动机组 Gi的最大临界热启动时间约束为

式中，Ts,i为Gi的启动时刻；TCH,i为Gi的最大临界热启动时间。

冷启动机组 Gi的最小临界启动时间约束为

式中，TCC,i为冷启动机组 Gi的最小临界启动时间。

（2）单个负荷最大功率约束。每一时步投入的最大单个负荷功率应小于本时步系统可承受的最大单个负荷功率以保持已恢复系统的稳定性，使恢复过程能够顺利进行，其约束为

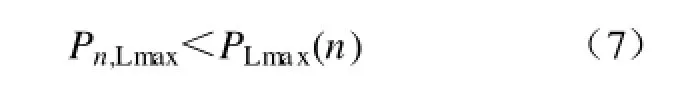
式中，Pn,Lmax为第 n时步投入的最大单个负荷，取机组最大单个厂用电负荷、PLⅠ,j、PLⅡ,j、PLⅢ,j中的最大值；PLmax(n)是第 n时步可恢复的单个最大负荷，本文采用文献[24]中的分段线性化方法计算各已并网机组的频率响应值，由机组的额定容量、频率响应值、最大允许频率下降值（取 0.5Hz）可计算出PLmax(n)。

（3）系统启动功率约束。每一时步被启动的机组所需启动功率与恢复负荷的功率之和应小于系统在此时步提供的启动功率，其约束为

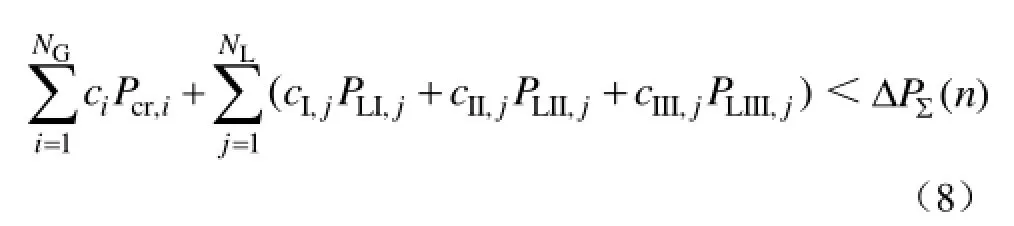
式中，Pcr,i为机组 Gi所需启动功率；为系统在第n时步可提供的启动功率，其值为该时步之前所有并网的机组在当前时步可增发的功率，即

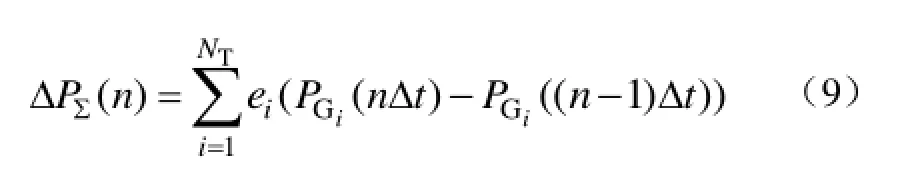
式中，ei为机组 Gi在当前时步是否已经并网发电，是取 1，否取 0；NT为系统中机组总数目，包含所有待启动机组和黑启动电源。

（4）系统运行约束。系统运行约束主要包括已恢复系统的有功平衡和无功平衡，机组有功、无功出力范围，节点电压上下限制和线路功率不越限等潮流约束。

3 多目标优化模型的求解

3.1 优化求解思路

在后续网架重构过程中，机组的恢复是基础，处在不同拓扑位置的机组快速启动可迅速扩展电源点分布，为更大范围的机组、更多重要负荷恢复优化创造条件，路径恢复为机组和负荷恢复提供功率，故机组、负荷和路径三者恢复的重要程度不同，具有层次关系，各优化目标之间优先级为FG＞FL＞FR，可采用分层序列法求解该多目标优化模型，机组恢复作为第一层优化目标，负荷恢复为第二层优化目标，路径恢复为第三层优化目标，分层后各层为单目标优化，也降低了求解复杂度。

模型的约束域是相互关联的，其中单个负荷的最大功率约束及机组的启动时间约束可通过负荷预选和机组预选来实现，通过对本时步优化得到的目标网络潮流校核可检验是否满足运行约束，故可将此模型松弛为由目标函数和机组启动功率约束构成的一维约束背包问题。以下由分层序列法结合改进细菌觅食算法和 Dijkstra算法对多目标网架重构模型具体求解。

3.2 机组层优化求解

细菌觅食算法是模拟人类大肠杆菌觅食行为的新型仿生算法[26]，主要通过趋化操作、复制操作和迁徙操作三种操作进行寻优。将细菌觅食算法应用于机组启动优化，由于机组有启动或不启动两种状态，细菌个体采用 0-1二进制编码，1表示相应机组启动，0表示不启动，并采用改进的趋化操作[27]，细菌个体随机选取两个位置，其中间的编码在操作中保持不变，其余位置编码随机发生变化，如果趋化后的新个体更优，则替换原个体。机组层优化采用预选与优选相结合方法，将当前时步满足启动条件的机组预选为备选待启动机组，再以改进细菌觅食算法对备选机组优化确定最优机组，主要步骤为：

（1）根据上一时步已恢复系统的状况，计算本时步系统可提供的启动功率及 PLmax(n)。

（2）将满足启动时间限制的厂用电最大单个功率小于PLmax(n)的还未启动机组 Gi放入集合P。

（3）细菌群体初始化，设置细菌个体数S，趋化操作次数 Nc、复制操作次数 Nre、迁徙次数 Ned及迁徙概率Ped，细菌编码长度为集合P中机组个数，适应度值取目标函数FG。

（4）对每一细菌个体趋化操作，比较趋化后个体与原个体适应度，若优于原个体，则替换原个体。

（5）全部个体趋化后，进入下一次趋化操作，直至达到指定趋化次数。

（6）对细菌个体按适应度排序，适应度较差的S/2个个体淘汰，剩下 S/2个个体复制。

（7）判断是否达到最大复制次数，是则转向步骤（8），否则转向步骤（4）。

（8）对每一细菌个体生成随机数，随机数小于迁徙概率的个体淘汰，并生成新的个体。

（9）判断是否达到最大迁徙次数，是则输出最优个体，否则转向步骤（4）。

3.3 负荷层优化求解

将上述改进细菌觅食算法应用于负荷优化，具体步骤如下：

（2）将单个负荷功率小于本时步 PLmax(n)、还未恢复的负荷作为本时步的备选待恢复负荷。

（3）初始化细菌种群，设置算法参数，个体长度取备选待恢复负荷数，目标函数取为FL。

（4）全部细菌个体完成指定次数的趋化操作。

（5）细菌个体复制操作，并判断是否达到最大复制次数，否则转向步骤（4），是则转向步骤（6）。

（6）细菌个体迁徙操作，并判断是否达到最大迁徙次数，否则转向步骤（4），是则输出最优个体。

3.4 路径恢复层的优化

路径恢复层的优化一方面为机组、负荷恢复提供合理的路径，另一方面也使系统中关键线路尽快恢复，为最终骨架网络目标打下基础。路径优化是由已恢复网络到待恢复的机组、负荷目标节点的最小支撑树问题，线路权值取为，路径优化按以下步骤进行：

（2）依欲恢复目标节点编号顺序调用 Dijkstra算法，为每一目标节点搜索恢复路径。

（3）将搜索到的目标节点恢复路径中权值最小的路径中所包含线路权值置为。

（4）判断本时步欲恢复目标节点是否恢复完毕，是则输出各目标节点权值最小的最优恢复路径；否则转向步骤（2）。

在分别求得本时步最优机组、负荷及恢复路径后，对本时步形成的目标网络潮流校验，以校核是否满足各种运行约束条件，若满足，则重构进入下一时步；若不满足，则适当修改已恢复路径上的负荷，重新进行校核，直到满足约束条件为止再进入下一时步。

由于采取总体协调的分时步策略优化后续网架重构，重构开始时总时间 T1未知，根据经验设T1=4h，进入重构第一时步，依次优化每一时步直至完成网架重构（设所有满足热启动时间条件的机组全部启动为网架重构结束标志）得到重构时间 T，若T1=T，网架重构结束；否则，置T1=T，再重新进行网架重构优化，直至两者值相等，完成重构。

4 扩展黑启动方案后效性评估

4.1 网架重构输入输出指标

以生产函数的角度分析，后续网架重构是多输入多输出的过程，输入为构建目标网架耗费的资源量，输出为目标网架，重构效率以直观量化形式综合测度不同重构方案输入输出不同引起的差异，可合理地表征扩展黑启动方案的后效性。

数据包络分析法（Data Envelop Analysis, DEA）是一种以数学规划模型评价多输入多输出决策单元相对有效性的非参数方法[28]，由于不需要预先对任何参数作假设及指标标准化处理，完全依据实际数据对决策单元评估，避免了主观因素的影响，评估结果更客观，为扩展黑启动方案的后续网架重构相对效率评估提供了有效工具。充分发挥DEA评估相对效率客观性的关键在于选择合理的输入输出指标集，结合指标选取应遵循的科学性、适用性和系统性等基本原则与网架重构的具体特点，选取以下的输入输出指标。

4.1.1 输入指标

（1）机组和负荷恢复所需功率Pcr∑。后续网架重构各时步恢复的机组所需启动功率与负荷功率加权和。即

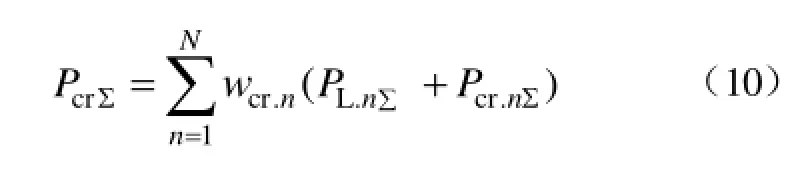
式中，N为网架重构时步数；PL.n∑为 n时步恢复的负荷总量；Pcr.n∑为n时步启动的机组启动功率和；wcr.n为 n时步启动功率的权值，取值随时步增加而减小。

（2）恢复路径指标 Lc。为机组、负荷恢复提供启动功率的路径指标定义为

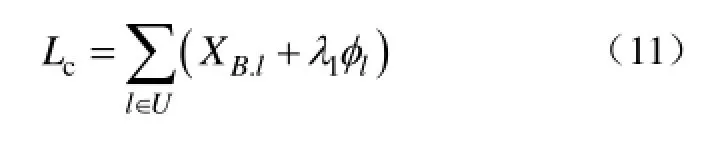
式中，U为最终目标网架恢复的所有线路集合。

（3）网架重构总时间Ts。网架重构耗费总时间，为各时步时长之和。

4.1.2 输出指标

（1）启动机组总容量 PG∑。以各时步启动机组容量的加权和表示为

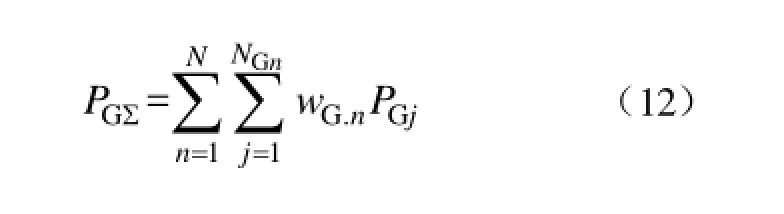
式中，NGn为时步n恢复的机组数；wG.n为n时步启动的机组容量权值，随着时步的增加而减小；PGj为n时步恢复的第j台机组额定容量。

（2）恢复负荷总量 PL∑。负荷总量以各时步恢复的负荷节点中各类负荷的加权和表示为

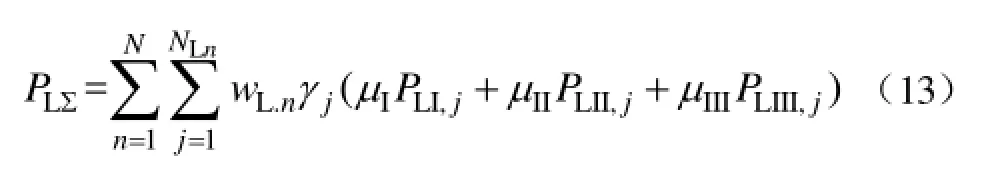
式中，NLn为时步n恢复的负荷数；wL.n为时步n恢复负荷的权值，取值随时步增加而减小。

（3）骨干网络度 Mnet。以骨干网络度来综合衡量最终目标网架结构特征属性，将Mnet定义为

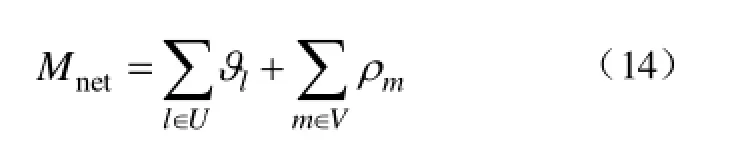
4.2 网架重构相对效率评估

DEA中基本 CCR模型的局限性是无法对效率值都为1的有效决策单元进一步区分效率高低，随后 Andersen等提出的将被评单元从参考集内移去的超效率数据包络分析模型（Super Efficiency DEA）克服了该缺陷，可实现对所有决策单元的全部排序。

假设有Q个扩展黑启动后续网架重构方案，对于某一方案Dk，评价其相对效率具有非阿基米德无穷小的输入型SE-DEA模型为

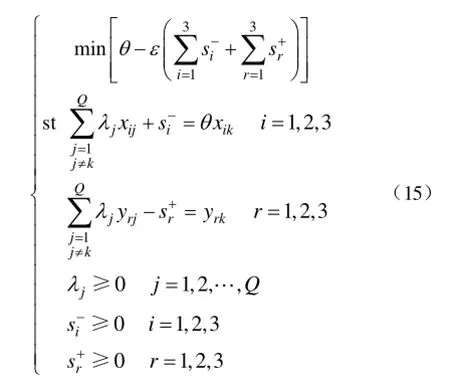
式中，θ为被评价方案 Dk的相对效率值；λj为输入输出指标的权重系数；si-、sr+为松弛变量；ε为非阿基米德无穷小量，一般取10-6；xij和yrj分别为方案 Dj中第i个输入指标值和第 r个输出指标值；xik和 yrk分别为方案 Dk中第 i个输入指标值和第r个输出指标值。采用 SE-DEA模型评估网架重构方案时，以客观的输入输出指标数据为依据，以数学规划方法求取方案的相对效率值作为决策依据信息。

4.3 扩展黑启动方案后效性评估流程

综合上述多目标网架重构模型和 SE-DEA 模型，扩展黑启动方案后效性评估流程如图 2所示。

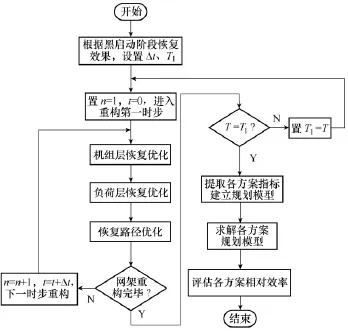
图2 扩展黑启动方案后效性评估流程Fig.2 Aftereffect evaluation process of extended black-start schemes

5 算例分析

5.1 算例描述

为了验证本文方法的有效性，以新英格兰 10机 39节点系统为例对扩展黑启动方案后效性进行研究。设33节点为大型抽水蓄能电站，将其作为黑启动电源，各被启动机组参数如表1所示，假设31节点机组具有冷启动时限，最小临界时限为4h，其余机组最大临界热启动时间为1.5h，通过技术校验合格的三套扩展黑启动方案如表2所示。算法参数设置为：S=50，Nc=10，Nre=5，Ned=5，Ped=0.5。

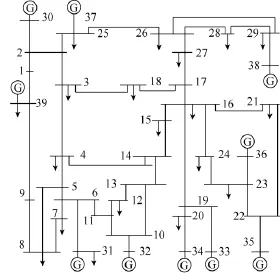
图3 新英格兰10机39节点系统Fig.3 New England 10-unit 39-bus power system

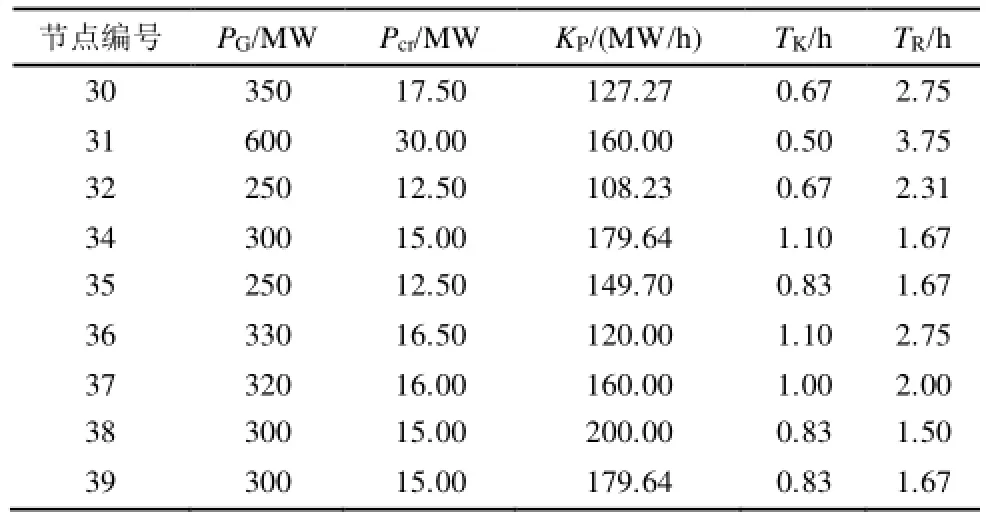
表1 被启动机组的启动参数Tab.1 Parameters of the units to be restored

表2 技术可行的扩展黑启动方案Tab.2 Technically feasible extended black-start schemes

5.2 计算结果

利用本文构建的多目标网架重构模型在表2中各不同扩展黑启动方案黑启动阶段形成的局部网络基础上进行网架重构，得到各自后续网架重构方案如表3所示。

表3 各扩展黑启动方案后续的网架重构方案Tab.3 The subsequent network reconstruction schemes based on different extended black-start schemes

权重系数wcr.n、wG.n和wL.n第一时步取1，第二时步取 0.6，计算出不同的扩展黑启动方案下网架重构的输入输出指标值如表 4所示。

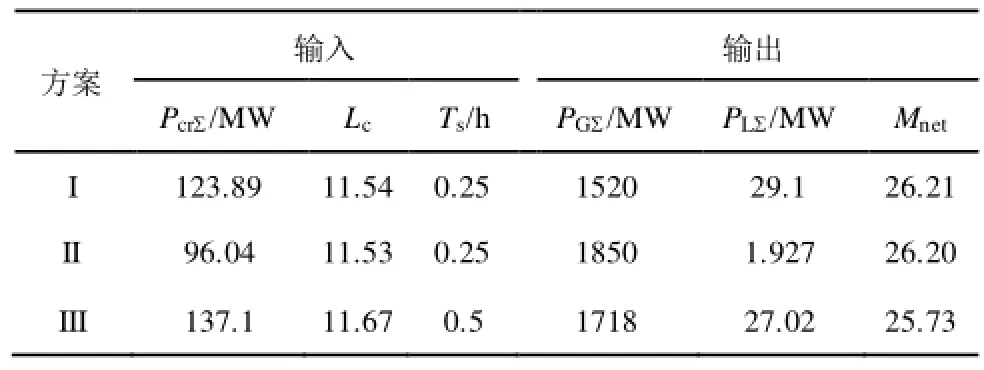
表4 各恢复方案的输入输出指标值Tab. 4 The inputs and outputs of all restoration plans

按照输入型SE-DEA模型式（15）分别对各个重构方案建立评估模型，利用规划软件 lingo进行求解，得到各个方案的相对效率评估结果如表5所示。

表5 各恢复方案的相对效率评估结果Tab.5 The assessment results of relative efficiency for all restoration plans

5.3 结果分析

从表2～表4中可以看出，方案I形成的小系统包含4台机组，其一个时步即可启动所有待恢复机组及部分重要负荷完成网架重构；方案II与方案 III都是由黑启动电源启动2台机组，但方案III中 32号机组升负荷率较方案 II中 35号机组慢，在其启动后为后续恢复提供的功率较小，方案II一步即可完成网架重构，而方案 III需要两步才能完成。故综合考虑了网架重构多输入多输出要素后的相对效率评估结果中，方案I效率最高，方案II次之，方案III效率第三。对每一方案的各个时步恢复过程进行潮流校验，方案 I最高电压为 U22=1.071(pu)；方案II最高电压为 U29=1.09(pu)；方案 III最高电压为U19=1.06(pu)，均满足系统运行条件的约束。

通过对三个不同扩展黑启动方案后效性评估可知后续网架重构的效率与黑启动阶段形成的小网络机组容量、机组特性、网络节点的拓扑位置等因素密切相关，包含的机组越多，机组升负荷率越快，容量越大，节点越重要，为后续恢复提供的功率越大，恢复的时间越短，效率越高。在综合选择扩展黑启动方案时，不仅要考虑黑启动恢复初期阶段效果，还要计及对后续恢复的影响，选择综合效果好的方案，本文提出的扩展黑启动后效性评估方法能够有效评估后续网架重构效率，进一步完善了扩展黑启动方案的评估体系。

5 结论

本文提出了基于多目标网架重构模型与超效率数据包络分析模型相结合的扩展黑启动方案后效性评估方法。采用总体协调的分时步重构策略可从全局整体最优角度优化得到每一时步的恢复措施进而完成重构过程得到目标网架，所构建的多目标网架重构模型可有效兼顾机组、负荷及路径的协调恢复；建立的指标体系能够全面系统反映网架重构的多输入输出特征，超效率数据包络分析模型对表征扩展黑启动方案后效性的后续网架重构相对效率客观评估。算例分析结果验证了所提方法的正确性与有效性，对恢复方案的综合决策提供重要参考。

[1] 张东霞, 姚良忠, 马文媛. 中外智能电网发展战略[J]. 中国电机工程学报, 2013, 33(31): 1-14.

Zhang Dongxia, Yao Liangzhong, Ma Wenyuan. Development strategies of smart grid in China and abroad [J]. Proceedings of the CSEE, 2013, 33(31): 1-14.

[2] 薛禹胜, 肖世杰. 综合防御高风险的小概率事件[J].电力系统自动化, 2011, 35(8): 1-11.

Xue Yusheng, Xiao Shijie. Comprehensively defending high risk events with low probability[J]. Automation of Electric Power Systems, 2011, 35(8): 1-11.

[3] 汤涌, 卜广全, 易俊. 印度“7. 30”、“7. 31”大停电事故分析及启示[J]. 中国电机工程学报, 2012, 32(25): 167-174.

Tang Yong, Bu Guangquan, Yi Jun. Analysis and lessons of the blackout in indian power grid on july 30 and 31, 2012[J]. Proceedings of the CSEE, 2012, 32(25): 167-174.

[4] 毛安家, 张戈力, 吕跃春, 等. 2011年9月8日美墨大停电事故的分析及其对我国电力调度运行管理的启示[J]. 电网技术, 2012, 36(4): 74-78.

Mao Anjia, Zhang Geli, Lv Yuechun, et al. Analysis on large-scale blackout occurred in south america and north mexico interconnected power grid on sept. 8, 2011 and lessons for electric power dispatching in China[J]. Power System Technology, 2012, 36(4): 74-78.

[5] Adibi M M, Fink L H. Power system restoration planning[J]. IEEE Transactions on Power Systems, 1994, 9(1): 22-28.

[6] Lester H F, Lion K L, Liu C C. From generic restoration to specific restoration strategies[J]. IEEE Trans. on Power Systems, 1995, 10(2): 745-752.

[7] Jerry J A. A framework for power system restoration following a major power failure[J]. IEEE Transactions on Power Systems, 1995, 10(3): 1480-1485.

[8] Gomes R, Carlos A, Guarini A. Guidelines for power system restoration in the brazilian system[J]. IEEE Transactions on Power Systems, 2004, 9(2): 1159-1164.

[9] Delfino B, Denegri G B, Invernizzi M, et al. Blackstart and restoration of a part of the Italian HV network: modeling and simulation of a field test[J]. IEEE Trans. on Power Systems, 1996, 11(3): 1371-1379.

[10] 张玉琼, 顾雪平. 基于随机统计分析的黑启动操作过电压的计算校验[J]. 电工技术学报, 2005, 20(5): 92-97.

Zhang Yuqiong, Gu Xueping. Computation and statistical evaluation of operating over voltages in blackstart process of power systems[J]. Transactions of China Electrotechnical Society, 2005, 20(5): 92-97.

[11] 吴烨, 房鑫炎. 基于模糊 DEA 模型的电网黑启动方案评估优化算法[J]. 电工技术学报, 2008, 23(8): 101-106.

Wu Ye, Fang Xinyan. Data envelopment analysis based optimal fuzzy algorithm for assessing power grid black-start plans[J]. Transactions of China Electrotechnical Society, 2008, 23(8): 101-106.

[12] 林振智, 文福拴, 薛禹胜, 等. 基于多属性群决策特征根法的智能电网黑启动决策[J]. 电力系统自动化, 2010, 34(5): 18-23.

Lin Zhenzhi, Wen Fushuan, Xue Yusheng, et al. Blackstart decision-making in smart grids using muti-attribute group eigenvalue method[J]. Automation of Electric Power Systems, 2010, 34(5): 18-23.

[13] 吴烨, 房鑫炎, 张焰, 等. 电网黑启动的广义模式评估算法[J]. 电工技术学报, 2011, 26(3): 155-161.

Wu Ye, Fang Xinyan, Zhang Yan, et al. Generalized assessment algorithm for power grid black-start modes [J]. Transactions of China Electrotechnical Society, 2011, 26(3): 155-161.

[14] 林济铿, 李童飞, 赵子明, 等. 基于熵权模糊综合评价模型的电力系统黑启动方案评估[J]. 电网技术, 2012, 36(2): 115-120.

Lin Jikeng, Li Tongfei, Zhao Ziming, et al. Assessment on power system black-start schemes based onentropy weighted fuzzy comprehensive evaluation model[J]. Power System Technology, 2012, 36(2): 115-120.

[15] 顾雪平, 钟慧荣, 贾京华, 等. 电力系统扩展黑启动方案的研究[J]. 中国电机工程学报, 2011, 31(28): 25-32.

Gu Xueping, Zhong Huirong, Jia Jinghua, et al. Extended black-start schemes of power systems[J]. Proceedings of the CSEE, 2011, 31(28): 25-32.

[16] Liu Yan, Gu Xueping. Skeleton network reconfiguration based on topological characteristics of scalefree networks and discrete particle swarm optimization [J]. IEEE Transactions on Power Systems, 2007, 22(3): 1267-1274.

[17] 王亮, 刘艳, 顾雪平, 等. 综合考虑节点重要度和线路介数的网络重构[J]. 电力系统自动化, 2010, 34(12): 29-33.

Wang Liang, Liu Yan, Gu Xueping, et al. Skeleton network reconfiguration based on node importance and line betweenness[J]. Automation of Electric Power Systems, 2010, 34(12): 29-33.

[18] 周云海, 闵勇. 恢复控制中的系统重构优化算法研究[J]. 中国电机工程学报, 2003, 23(4): 67-71.

Zhou Yunhai, Min Yong. Optimal algorithm for system reconstruction[J]. Proceedings of the CSEE, 2003, 23(4): 67-71.

[19] 刘强, 石立宝, 倪以信, 等. 电力系统恢复控制的网络重构智能优化策略[J]. 中国电机工程学报, 2009, 29(13): 8-15.

Liu Qiang, Shi Libao, Ni Yixin, et al. Intelligent optimization strategy of the power grid reconfiguration during power system restoration[J]. Proceedings of the CSEE, 2009, 29(13): 8-15.

[20] 林振智, 文福拴. 基于加权复杂网络模型的恢复路径优化方法[J]. 电力系统自动化, 2009, 33(6): 11-15, 103.

Lin Zhenzhi, Wen Fushuan. A new optimization method for determining restoration paths based on weighted complex network model[J]. Automation of Electric Power Systems, 2009, 33(6): 11-15, 103.

[21] 周云海, 刘映尚, 胡翔勇. 大停电事故后的系统网架恢复[J]. 中国电机工程学报, 2008, 28(10): 32-36.

Zhou Yunhai, Liu Yingshang, Hu Xiangyong. Power system network reconstruction after blackout[J]. Proceedings of the CSEE, 2008, 28(10): 32-36.

[22] 王洪涛, 刘玉田. 电力系统恢复的主从递阶决策模型及其优化算法[J]. 中国电机工程学报, 2007, 27(1): 8-13.

Wang Hongtao, Liu Yutian. Leader-follower hierarchical decision model and optimal method for power system restoration[J]. Proceedings of the CSEE, 2007, 27(1): 8-13.

[23] 王洪涛, 刘玉田. 基于 NSGA-Ⅱ的多目标输电网架最优重构[J]. 电力系统自动化, 2009, 33(23): 14-18.

Wang Hongtao, Liu Yutian. Multi-objective optimization of power system reconstruction based on NSGAII[J]. Automation of Electric Power Systems, 2009, 33(23): 14-18.

[24] Gu X, Zhong H. Optimisation of network reconfiguration based on a two-layer unit-restarting framework for power system restoration[J]. IET Generation, Transmission & Distribution, 2011, 6(7): 693-700.

[25] Zhang Can, Lin Zhenzhi, Wen Fushuan, et al. Two stage power network reconfiguration strategy considering node importance and restored generation capacity [J]. IET Generation, Transmission & Distribution, 2014, 8(1): 91-103.

[26] Passino K M. Biomimicry of bacterial foraging for distributed optimization and control[J]. IEEE Control Systems Magazine, 2002, 22(6): 52-67.

[27] 戴秋萍, 马良, 郗莹. 求解0-1背包问题的细菌觅食算法[J]. 数学的实践与认识, 2013, 43(3): 178-183.

Dai Qiuping, Ma Liang, Xi Ying. Bacterial foraging algorithm for 0-1 knapsack problem[J]. Mathematics in Practice and Theory, 2013, 43(3): 178-183.

[28] 马占新. 数据包络分析模型与方法[M]. 北京: 科学出版社, 2010.

Investigation on Aftereffect of Power System Extended Black-Start Schemes

Gu Xueping1 Wang Dajiang1 Li Shaoyan1 Li Wenyun2 Zhu Tao2 Zhao Chuan2

（1. State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources North China Electric Power University Baoding 071003 China 2. Yunnan Electric Power Dispatching and Control Center Kunming 650011 China）

The extended black-start strategy during the early recovery stage after blackout provides a new way for power system restoration. In order to evaluate the aft ereffect of an extended black-start scheme, through discretizing the network reconstruction process into a series of successive time steps, a multi-objective network reconstruction optimization model considering the alternation and coordination that unit restarting with load restoration during subsequent reconstruction process is established, and then a solving method combining the lexicographic optimization method with improved bacterial foraging algorithm and Dijkstra algorithm is proposed to solve the model. The units, loads and restoration paths in each time step are optimized from the perspective of the global optimum to obtain the optimal reconstruction scheme. After that, by defining a group of input and output indexes reflecting the multiple elements of reconstruction process, the relative efficiency of the subsequent reconstruction, which represents the aftereffect of the extended black-start scheme, are evaluated by using the super efficiency data envelopment analysis model. The test results on the New England 10-unit 39-bus system verified the validity and correctness of the proposed method.

Extended black-start, aftereffect, data envelop analysis, network reconstruction, multi-objective optimization

TM76

顾雪平 男，1964年生，教授，博士生导师，主要研究方向为电力系统安全防御与恢复控制、智能技术在电力系统中的应用。

国家自然科学基金（51277076），高等学校博士学科点专项科研基金（20110036110007）和中央高校基本科研业务费专项资金（13XS23）资助项目。

2014-06-19 改稿日期 2014-12-24

王大江 男，1984年生，博士研究生，研究方向为电力系统安全防御与恢复控制。