直流偏磁对变压器振动噪声的影响

王佳音 白保东 刘宏亮 马 闯

直流偏磁对变压器振动噪声的影响

王佳音 白保东 刘宏亮 马 闯

（沈阳工业大学现代电工装备理论与共性技术重点实验室 沈阳 110870）

取向硅钢片的磁致伸缩特性是引起变压器振动噪声的主要原因，并且直流偏磁在很大程度上加剧了变压器的振动噪声。本文首先测量了取向硅钢在不同磁密下的磁致伸缩蝴蝶曲线族，研究了轧制方向（RD）和垂直轧制方向（TD）磁致伸缩的特性，同时研究了直流偏磁对磁致伸缩特性的影响，然后用平均磁致伸缩曲线来模拟取向硅钢片的磁致伸缩特性，并将其应用到直流偏磁条件下一台 160kV·A干式变压器空载振动的有限元计算。最后实验测量了直流偏磁条件下变压器铁心不同位置的空载振动，以及随着直流偏磁的增大，噪声声压级的值。综合有限元计算和实验测得的空载振动噪声值，分析了直流偏磁对变压器振动噪声的影响。

磁致伸缩 直流偏磁 振动 噪声

1 引言

磁致伸缩是铁磁材料的重要特性之一，在磁化的过程中会引起铁磁材料本身尺寸的变化，在交变的电磁场下，磁致伸缩会引起铁磁材料的周期性振动，所以磁致伸缩是电力变压器和电机等设备振动噪声的主要来源。我国地域宽广，电网现采用的直流输电方式以及地磁变化等原因都会引起电力变压器中性点电位升高，从而引起电力变压器发生直流偏磁现象，使电力变压器励磁电流畸变，铁心饱和，同时也影响铁心硅钢片的磁致伸缩特性，导致直流偏磁条件下电力变压器振动噪声加剧，这是直流偏磁现象最主要的不良后果。

国内外的很多学者关于软磁材料的磁致伸缩做了大量的研究工作，2006年 R.Grossinger等学者提出了一种精确测量磁致伸缩的方法[1]。Sakda Somkun等学者在2012年对旋转磁通作用下的无取向硅钢片的二维磁致伸缩特性进了模拟和测量[2]，主要应用于电机振动噪声的研究中。也有一些国外学者在应用磁致伸缩计算铁磁材料的振动噪声方面做了很多的研究工作，Tom Hilgert等人在2008年提出了模拟磁致伸缩的数学模型，并应用到磁芯振动噪声的计算中[3]。2011年 Pan Seok Shin and Hee Jun Cheng通过磁场和机械力场的耦合方程计算了变压器和电机的磁致伸缩力，位移，以及变压器的模态振型[4]。一些国外学者详细研究了磁致伸缩特性以及电力变压器振动噪声的来源和产生机理，认为磁致伸缩是产生变压器振动噪声的主要原因[5,6]。直流偏磁现象是直流输电引起的不利影响，我国很多学者关于直流偏磁现象做了大量的研究工作，分析了直流偏磁产生的原因，以及其给电力变压器带来的诸多不利影响，主要包括励磁电流畸变，甚至引起绝缘损坏等，最重要的是直流偏磁引起变压器振动噪声的增大[7-9]。我国关于变压器用取向硅钢片的磁致伸缩特性的研究起步较晚，值得进一步深入研究，而且基于磁致伸缩特性计算变压器振动噪声的方法可借鉴的较少，大部分的研究忽略磁致伸缩的影响，只考虑电磁力引起的振动噪声。本文在准确测量取向硅钢片磁致伸缩的特性的基础上，采用有限元的方法计算了变压器的振动噪声。

本文首先精确测量了用于变压器生产制造的取向硅钢片 RD和 TD方向的磁致伸缩特性，为了用于有限元的计算，根据测量得到的磁致伸缩回环，通过拟合插值的方法得到了 RD和 TD方向的单值磁致伸缩特性曲线，然后通过商用软件计算了直流偏磁条件下一台160kV·A变压器的振动噪声，详细分析了直流偏磁对变压器振动噪声的影响，最后进行了不同直流偏磁条件下该变压器的空载振动噪声实验，详细分析了直流偏磁对变压器振动噪声的影响，验证了仿真分析方法的有效性。

2 磁致伸缩特性测量

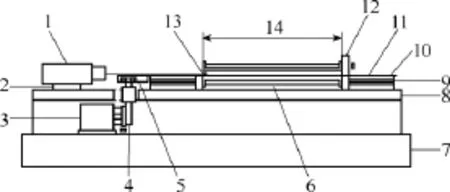
图1 测量磁致伸缩设备结构示意图Fig.1 Configuration of measurement device

磁致伸缩测量装置由德国 Brockhaus制造，符合国际标准 IEC/TR62581[10]，设备的具体结构如图 1所示。本文的测试样片为用于变压器制造的30ZH120取向硅钢片，样片的有效大小为 500mm×100mm，其一端由设备的夹件固定，在自由伸长的另一端固定反光镜，配和激光发射装置测量样片的磁致伸缩，灵敏度为10nm/m。一次侧激励线圈施加工频50Hz正弦电压。

磁致伸缩是一种尺寸变化现象，当通过变压器铁心电工钢片内部的磁通发生变化时会引起电工钢片本身尺寸的变化。当磁通达到某个典型值时，在变压器正常工作条件下，其每米的形变量为 10-2～10-5m。磁致伸缩随外部磁场的变化而变化。图 2a给出了引起硅钢片磁致伸缩的磁通密度 B的曲线，磁通密度B和磁通的变化率成正比，所以磁通密度B按正弦规律变化，磁通密度的最大值Bmax分别为0.2T到1.8T，步长为0.1T，图2a给出了Bmax分别为0.6T、0.9T、1.2T、1.5T时，一个时间周期的磁密变化规律，根据安培定律，由励磁电流可以计算出相应磁场强度 H的变化规律，如图 2b所示，可以发现，当Bmax为1.5T磁场H开始出现饱和现象，磁场开始出现饱和现象。

图2 磁通密度和磁场强度的时间特性曲线Fig.2 Waveforms of B and H

图3 在施加50Hz完整周期时不同峰值磁密Bmax=0.2～1.8T时的磁致伸缩长度相对变化曲线Fig.3 Magnetostriction loop under 50Hz alternating magnetization for Bmaxof 0.2 to1.8T

图 3中每个蝴蝶曲线表示为磁致伸缩与工频50Hz时磁通密度 Bmax的对应关系。蝴蝶曲线的磁通密度 Bmax从 0.2T开始，以 0.1T为步长依次增加到1.8T，其方向和样片RD一致。此时的测量值为样片RD的磁致伸缩特性。改变样片的剪裁角度，也测量了TD的磁致伸缩特性。随着 Bmax的增大，蝴蝶曲线的“翅膀”也在不断的变宽，变大。

当磁通密度 Bmax分别为 0.7T和 1.7T，分别绘制了RD和TD的磁致伸缩极坐标曲线，如图4所示。磁致伸缩的最大伸长量λ+和最大收缩量λ-随着 B的增大而增大，从图中可以看出取向硅钢30ZH120的磁致伸缩各向异性特性明显，相同磁通密度条件下，TD的λ+以及λ-的远远高于RD的数十倍。这些数据用来研究变压器叠片接缝处的噪声增大原因。

图4 磁通密度Bmax= 0.7T和1.6T时磁致伸缩在极坐标下的图形Fig.4 Magnetostriction for Bmaxof 0.7T and 1.6T at the polar coordinate

用于有限元计算的磁致伸缩曲线应该是单值的，因此需要根据蝴蝶曲线族拟合一条单值磁致伸缩特性曲线。选取 RD和 TD磁致伸缩特性曲线族中的每个蝴蝶曲线最大伸长量 λ+和引起该形变量的磁通密度B，分别得到一组（λ+，B）数据，用来描述样片两个方向的磁致伸缩特性，通过B样条插值的方法，然后得到两条光滑的并适用于有限元计算的磁致伸缩单值曲线，如图 5所示。

图5 磁致伸缩单值曲线Fig.5 Single-valued magnetostrictive curves

图6 表示磁通密度分别为 Bmax=0.6T、0.9T、1.2 T、1.5T、频率为50Hz时磁致伸缩的震荡变化曲线。在励磁磁场按正弦规律变化的一个时间周期内，磁致伸缩相应的变化了两周期，磁致伸缩引起的长度变化率与磁通密度的极性无关，只与其幅值和钢材结晶轴之间的相对方向有关，因此，在正弦波磁通励磁下，长度变化的基波频率为励磁电压频率的两倍。磁致伸缩随着磁通密度的变化呈非线性变化，尤其在磁密值接近饱和的情况下，这种效应很明显是非线性的。非线性将在铁心振动频谱中产生一个明显的谐波分量。其周期为励磁频率（连同其谐波）的两倍。

图6 磁致伸缩波形Fig.6 Waveforms of magnetostriction

在一个磁场时间周期内磁致伸缩的最大伸长量λ+和最大收缩量 λ—保持不变，所以磁致伸缩的蝴蝶曲线是左右对称的，磁致伸缩受直流偏磁的影响较大，当样片中存在直流偏磁时，磁致伸缩蝴蝶曲线失去了左右对称性，并且加深了磁致伸缩的饱和特性，这也将进一步影响变压器的振动噪声。

3 变压器振动噪声的有限元计算

铁心是变压器最主要的部件之一，既为磁通提供磁路，也是安装线圈的骨架，对变压器的电磁性能、机械强度等起着至关重要的作用，同时铁心也是变压器最主要的振动噪声源。因此，对电力变压器的铁心进行仿真计算研究是降低铁心振动噪声很重要的一部分，铁心振动的有限元计算是一个电路，磁场，结构力场以及声场多物理场耦合问题。当考虑直流偏磁对其的影响时，问题变得更为复杂。

本文通过商用软件计算了一台 160kV·A,干式单相四柱式变压器在直流偏磁情况下的铁心的振动位移，变压器一次侧施加 400V，50Hz交流额定电压，并设置直流偏置电压0.7V，将交流电压源置零时，得到回路中的直流电流 Idc=1.9A，变压器二次侧开路，模拟变压器空载运行工况。图5中的磁致伸缩单值曲线用来模拟磁致伸缩引起的形变，从而考虑了磁致伸缩引起的振动。图7给出此时铁心的振动位移，红色区域的位移最大值为0.324 8μm，蓝色区域的最小位移为0μm，这与仿真计算时设置的底部固定约束条件一致。当铁心中存在直流磁通时的最大位移比没有直流磁通时的 0.296 2μm增大了 9.66%。这也验证了直流偏磁确实引起了变压器铁心振动噪声的增大。

图7 直流偏磁为1.9A时铁心振动位移图Fig.7 Vibration displacements for DC current at 1.9A

其中变压器器身上某点的振动位移时域波形如图8所示，时间从 1.76s到 1.80s，历史 0.04s，为该点在两个时间周期内的振动位移规律。其规律符合物理的实际的振动特性。将该点的振动时域波形，进行傅里叶变化得到振动的频谱图，如图9所示，振动频率主要集中在50Hz、100Hz、150Hz、200Hz、250Hz、300Hz、400Hz、450Hz处，这与直流偏磁引起变压器奇次谐波含量增加的事实相符。在其他频率处也有谐波的少量存在，可能是模型在计算时，剖分不够精细引起的。

图8 振动位移时域波形Fig.8 Vibration versus time

图9 振动位移频域波形Fig.9 Vibration spectrum

4 实验研究不同直流偏磁条件下的变压器空载振动噪声

4.1 实验设计

为了验证上述有限元计算振动噪声方法的正确性，分别进行了不同直流偏磁条件下的变压器的空载振动和噪声实验。振动实验采用的设备是由德国PRUFTECHNIK公司生产的VIBXPERT®Ⅱ型FFT数据采集&信号分析仪，该仪器可以双通道同时对时域振动信号采集，并且进行FFT频谱分析，可同时采集位移，速度和加速度的时域和频域信号等，噪声测量实验采用的是丹麦B&K公司生产的2250手持式噪声分析仪，测试范围为 20～140dB。

本文实验对象为两台参数一致，容量为160kV·A变压器，一次侧额定电压为400V，二次侧额定电压为2 000V，单项四柱式。实验变压器的结构如图10所示，为了在变压器内产生直流偏磁磁通，设计实验电路图如图 11所示，首先两台变压器的低压侧并联，通过调压器施加额定 400V，50Hz交流电压，然后将高压侧反向串联，用来抵消二次侧感应电压，最后串联（15V，5A）的直流电压源，同时串联（11Ω，10A）的滑动变阻器，使直流的调节范围为1～5A，从而在变压器铁心中引入不同大小的直流偏磁磁通。

图10 实验变压器的振动选点原则Fig.10 Transformer model and testing points

图11 振动噪声实验电路图Fig.11 Circuit of experiment of vibration and noise

由于在进行直流偏磁条件下的变压器空载振动实验时，两台变压器同时运行，所以测量的噪声为两台变压器的噪声和，并不符合实验要求，因此定制了专门的噪声隔音罩，减小其中一台变压器的噪声10dB以上，此时测量的噪声值则为另一台变压器的噪声。如图 12所示。

图12 噪声隔音罩Fig.12 Soundproofing device

4.2 实验结果

实验变压器的结构对称，磁通密度云图分布对称，实验变压器底部固定，所以在进行直流偏磁条件下的振动实验时，选取变压器的 1/2器身作为实验对象，首先选取 16个振动数据采集点，如图 10所示，其中1～6号测试点位于铁心的上轭，由中间向端部依次分布，7～10号测试点位于上夹件处，由中间向两侧依次分布，11～13号点位于变压器铁心的旁轭正面，由上至下依次分布，14～16号测试点位于旁轭侧面，由上至下依次分布，测试点的选取充分考虑了铁心的整体结构。

调节实验变压器二次侧的反向串联电路中的滑动变阻器，使回路的直流电流Idc=0A、1A、2A、3A。分别采集四种直流偏磁状态下1～16号测试点的振动数据，包括振动速度的均方根值，振动位移的均方根值，以及速度和位移的时域和频域信号。其中图 13出了当 Idc分别为 0A、1A、2A、3A时，16个不同测试点的振动速度的均方根值以及振动位移的均方根值。

图13 1～16号测试点的振动速度和位移均方根值Fig.13 RMS of vibration velocity and displacement on 16 testing points

从图中可以看出，直流偏磁确实引起变压器空载振动的增大，直流偏磁加剧了 5、6、7、8、9、10、13、14、15、16号测试点的振动，并且其振动强度随着直流偏磁的增大而增大。3、4、11号测试点受直流偏磁的影响而增大，但随直流的变化规律不明显。但是并不是所有测点的振动都增大，其中1和 2号测试点在直流偏磁条件下振动减小，并随着直流偏磁的增大振动也增大。12号测点在直流偏磁为 2A时增大明显，可能是受变压器本身结构和模态固有频率的影响。并且11和12号测试点的振动明显大于其他各点，主要是因为其位于旁轭。没有夹件等结构件制约其振动。

以7号测试点为例分析了直流偏磁对振动速度频谱的影响，图14给出了直流偏磁电流Idc=0A、1A、3A时基频100H倍频频谱，以及其各次谐波的频谱含量图。如图中可以看出随着直流偏磁的增大基频100H倍频频谱所占的比例不断下降，如下表第 2行所示，由无直流偏磁时的 82.46%，下降到 47.07%和45.68%，奇次谐波的含量不断加大。同时给出了50Hz、150Hz、250Hz、350Hz谐波含量的增大的情况。

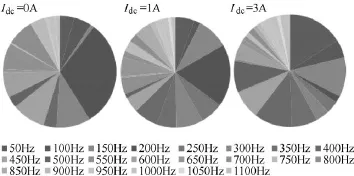
图14 7号测试点的各次频谱成分图Fig.14 Vibration spectrum of test No.7

表 直流偏磁对频谱含量的影响Tab. The spectrum contents under different DC bias

为了研究1号和2号测试点，直流偏磁条件下振动变小的原因，分析研究直流Idc分别为0A和1A时的频谱含量对比情况，如图15所示。不存在直流偏磁时 50Hz占优，但存在直流偏磁时，频谱在各个频谱点处都存在，尤其是出现了1 500Hz的频谱。这可能时振动烈度减小的原因。

图15 1号测试点不同直流偏磁条件下的频谱Fig.15 Vibration spectrum of test No.1 under DC current at 0Aand 1A

实验变压器的空载噪声随着直流偏磁的增大而增大，测量了直流电流 Idc从 0A以步长 0.5A增大到5A时的声压级，如图16所示，噪声声压级近似线性上升，当直流电流增大到5A时，噪声由57.3dB增大到 67.1dB，增大了 9.8dB。并且噪声的奇次谐波含量也增大了。

图16 空载噪声和直流偏磁大小的关系Fig.16 Sound pressure level of noise under DC currents

5 结论

本文在精确测量取向硅钢片磁致伸缩特性的基础上，开发了利用磁致伸缩单值曲线计算变压器振动的数值仿真方法，计算结果符合实际情况。通过实验研究，直流偏磁引起了变压器空载振动噪声的增大，但并不是引起所有测量点振动的增大，变压器铁心的振动受夹件等结构件的影响明显，直流偏磁引起了奇次谐波含量的增大，倍频频谱含量降低。并且随着直流偏磁的增大，变压器的空载噪声也不断地增大。

[1] Grö ssinger R, Sassik H, Holzer D, et al. Accurate measurement of the magnetostriction of soft magnetic materials[J]. Materials Science and Engineering, 2006, 131: 22-26.

[2] Sakda Somkun, Anthony J Moses, Philip I. Anderson, measurement and modeling of 2-D magneto-striction of nonoriented electrical steel[J]. IEEE Transactions of Magnetic, 2012, 48: 711-714.

[3] Tom Hilgert, Lieven Vandevelde, Jan Melkebeek. Comparison of magnetostriction models for use in calculations of vibrations in magnetic cores[J]. IEEE Transactions of Magnetic, 2008, 44(6): 874-877.

[4] Pan Seok Shin†, Hee Jun Cheung. A magnetostrictive force and vibration mode analysis of 3 kW BLDC motor by a magneto-mechanical coupling formulation [J]. Journal of Electrical Engineering & Technology, 2011, 6(1): 76-80.

[5] Moses J, Anderson P I, Phophongviwat T, et al. Contribution of magnetostriction to transformer noise [C]. UPEC2010, 2010.

[6] Weiser B, Pfü tzner H. Relevance of magnetostriction and forces for the generation of audible noise of transformer cores[J]. IEEE Transactions of Magnetics, 2000, 36: 3759-3777.

[7] 赵志刚, 刘福贵, 张俊杰, 等. 直流偏磁条件下变压器励磁电流的实验与分析[J]. 电工技术学报, 2010, 25(4): 71-76.

Zhao Zhigang, Liu Fugui, Zhang Junjie. Experiments and analyses of exciting current of transformer under DC bias[J]. Transactions of China Electrotechnical Society, 2010, 25(4): 71-76.

[8] 李泓志, 崔翔, 刘东升, 等. 直流偏磁对三相电力变压器的影响[J]. 电工技术学报, 2010, 25(5): 88-96.

Li Hongzhi, Cui Xiang, Liu Dongsheng, et al. Effect of DC bias on the three-phase power transformer[J]. Transactions of China Electrotechnical Society, 2010, 25(5): 88-96.

[9] 祝丽花, 杨庆新, 闫荣格, 等. 考虑磁致伸缩效应电力变压器振动噪声的研究[J]. 电工技术学报, 2013, 28(4), 1-6, 19.

Zhu Lihua, Yang Qingxin, Yan Rongge, et al. Research on vibration and noise of power transformers considering magnetostrictive effect[J]. Transactions of China Electrotechnical Society, 2013, 28(4), 1-6, 19.

[10] IEC/TR—62581: Electrical steel-methods of measurement of the magnetostriction characteristics by means of single sheet and epstein test specimens, 2010.

Research on Vibration and Noise of Transformers under DC Bias

Wang Jiayin Bai Baodong Liu Hongliang Ma Chuang

（Theory and Common Technologies of Modern Electrical Equipments Key Lab Shenyang University of Technology Shenyang 110870 China）

Magnetostriction in grain-oriented electrical silicon steel arises vibration and noise of the transformer core, especially when operating under direct current(DC) bias. In this paper, the anisotropy of magnetostriction of grain-oriented(GO) silicon steel sheets along the rolling direction (RD) and transversal direction(TD) deviating from RD 90° is measured based on a standard single sheet measurement system, and the single-valued curves of magnetostriction are obtained when incorporated with magnetic finite element(FE) analysis, then the vibrations are calculated through software. The vibration and noise are measured by experiments, the effect of DC bias on vibration and noise of transformer core is studied in detail.

Magnetostriction, DC bias, vibration, noise

TM412

王佳音 女，1987年生，博士研究生，主要研究方向为电气装备电磁场分析与优化设计。

国家自然科学基金（51277122），教育部创新团队项目（IRT1072）和教育部博士点基金（20122102130 001）资助项目。

2013-04-14 改稿日期 2014-06-14

白保东 男，1955年生，教授，博士生导师，主要研究方向为工程电磁场、电磁兼容、医学永磁机构。