基于矩阵填充技术重构低秩密度矩阵

韦仙

太原工业学院理学系，山西 太原 030008

基于矩阵填充技术重构低秩密度矩阵

韦仙

太原工业学院理学系，山西 太原 030008

从有限的信息中重构低秩或者近似低秩矩阵的问题日益受到人们的关注，解决这个问题的技术称为矩阵填充.对于一个希尔伯特空间下纯态或者近似纯态的量子体系（也就是低熵状态），其密度矩阵是低秩的，且迹为1.将矩阵填充理论应用于重构泡利测量下未知密度矩阵中，用Matlab软件程序进行数值模拟，采用奇异值阈值算法，将软阈值法则用在未知态密度矩阵的奇异值上，通过计算机编程，进行阈值迭代，直至达到截止标准，能够大大提高运行速率.由于以泡利矩阵为基的张量积结构便于在实验中获得，以重构泡利测量下的未知密度矩阵为例，采集了部分数据，分析了矩阵的重构结果.通过对重构误差、运行时间、采样率方面的研究，得出密度矩阵能够通过矩阵填充技术完整重构的结论.

矩阵填充；密度矩阵；低秩；量子态层析

0 引言

随着信息技术的飞速发展，重构量子态以及某些物理过程，在物理学、尤其量子信息科学领域的重要性日益增加［1］.而描述一个量子系统，最为普遍的方法是求解密度矩阵，它提供了一个量子态最完整的描述和解决方案［2］.因此，如何从可测量量中准确地重构密度矩阵，在科学研究上具有非常重要的意义.

重构泡利测量下密度矩阵的问题被普遍应用于量子态层析中，这是由于大多数物理过程关注的量子态都可用低秩密度矩阵准确描述，而且泡利基下的张量积结构容易在实验中测得.本文利用矩阵填充技术在泡利测量基础上能够有效地降低密度矩阵测量过程的复杂性，在一个矩阵可压缩或可稀疏表示时，通过观测矩阵的某种线性或非线性运算后的元素，来有效地重构出该矩阵.

1 相关技术

1.1 矩阵填充原理

矩阵填充原理是在压缩感知理论的基础上衍生发展的，于2006年兴起的压缩感知［3］理论，其核心思想是通过采集部分信息恢复傅里叶基下完整的稀疏信号.而现实研究中的信号通常可以用矩阵形式表示，若目标矩阵的特征值具有稀疏性（即低秩性）则可通过采集部分矩阵元恢复出完整的目标矩阵［4］，这就是衍生出的矩阵填充原理［5］.

矩阵填充主要研究的问题是：通过凸优化算法，仅采集部分数据和信息，有效地将目标矩阵准确重构出来.其具体的数学形式为：

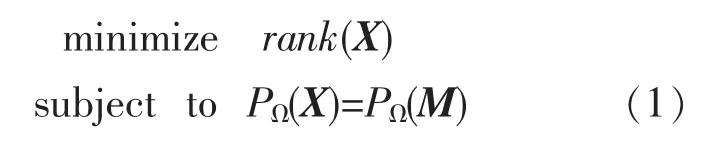
其中X表示重构矩阵，M表示原始目标矩阵，PΩ代表矩阵M的投影集合.

然而，根据（1）式，在秩最小化的条件下实现矩阵填充是一个NP－hard问题，则可把该问题转化为解决核范数最小化来重构未知矩阵：

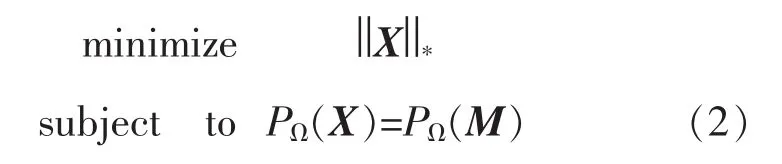
式（2）中||X||*为核范数，即奇异值之和，数学表达式为

任何理论都需要满足一定的条件才能实现，矩阵填充也不例外，从上述可知，要想利用矩阵填充原理重构目标矩阵，除了要满足矩阵的低秩性以外，在采样方式和数目上也有限制.

一般地，矩阵填充原理采取均匀等分方式采样；维数为d×d，秩为r的矩阵M，进行奇异值分解［6］（SVD），得矩阵M独立元的个数为r（2d－r）.如果采样数目m少于r（2d－r），那么无论采取何种采样方式都无法实现矩阵填充，也就是说，采样数目必须满足m≥r（2d－r）.

1.2 奇异值阈值（SVT）算法

在解决矩阵填充问题上，SVT算法是一种简单、易于实现的迭代算法，其核心是解决目标矩阵的凸优化问题，即核范数最小化问题.通过对矩阵的奇异值进行软阈值分解，选取合适的步长和阈值极限，SVT就能无限收敛接近于目标矩阵，该算法占用存储空间小、计算成本低，是重构低秩矩阵行之有效的方法［7］.

1.2.1 奇异值阈值（shrink）算子根据式（2）中，定义优化变量X∈Rd×d，取τ＞0，步长集合为｛δk｝k≥1，以Y0＝0∈Rd×d为起始，算法定义为：

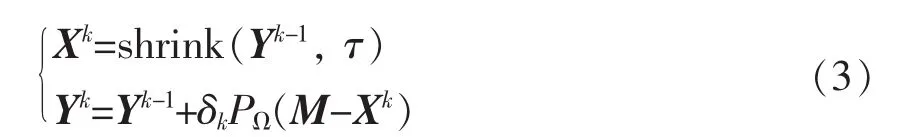
shrink（Yk－1，τ）是一种非线性函数，称为奇异值阈值算子，它是与核范数相关的近似操作，主要思想是将软阈值法则用到输入矩阵的奇异值上.

考虑秩为r的矩阵X∈Rd×d，奇异值分解式为

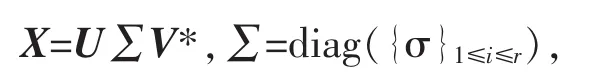
对于τ≥0，设软阈值算子Dτ作如下定义

其中t＋表示t的正数部分，即t＋＝max（0，t）.也就是说，这个操作是将软阈值法则用到矩阵X的奇异值上，从而有效地向零向量收缩.

1.2.2 阈值迭代下面介绍SVT算法，对于τ＞0数列｛δk｝为正的迭代步长，以Y0开始，k取值为k＝1，2，3…,式（3）变为

这个阈值迭代是比较容易实现.在每一步骤中，仅需计算奇异值（SVD）和执行初等矩阵运算即可.在标准的数值线性代数包的基础上，此算法用计算机编码就可实现.

定义非负整数l≤d，对于每组奇异向量有，

1.3 泡利测量下的密度矩阵

若一未知量子态是纯态或者近似纯态，则密度矩阵ρ∈Rd×d，秩为r，迹为1，其中希尔伯特空间维数d＝2n.设w1，w2，…，wd2为Rd×d中的标准正交基，对应于希尔伯特－施密特［8］（Hilbert－Schmidt）内积（A，B）＝tr（A*B），从｛w1，w2，…，wd2｝中随机均分采样出m个元素P1，P2，…，Pm，得观测系数（Pi，ρ），则可利用算法从这些数据中重构ρ.

表1 SVT算法具体步骤Table 1 The specific steps of SVT algorithm

由直积法则可知，w共有d2个矩阵元，记为w（a），a∈［1，d2］.从w（a）中随机采集m个元素S1，S2，…，Sm∈［1，d2］，从期望值trρw（Si）中重构密度矩阵.

为实现重构密度矩阵，要在矩阵空间上解决如下凸优化问题：

其中||λ||*是核范数，即奇异值之和.λ为通过凸优化重构的矩阵，与目标矩阵ρ相对应.

显然地，如果ρ在｛w（Si）｝基下几乎没有非零系数，那么SVT算法很难实现重构密度矩阵.为避免这种情况，必须保证运算过程中采集到ρ足够的重要信息，这就是很多文献中所提出的“不相关”概念.一般地，在某些特定的基（泡利基）下，任何低秩矩阵都是不相关的.

2 基于矩阵填充重构密度矩阵

本文利用矩阵填充优化算法，能够有效、快速地重构泡利测量下的密度矩阵.在核范数最小化的矩阵填充问题上，SVT算法主要是通过选择恰当的迭代步长使收敛集合无限接近于目标矩阵来实现重构.SVT算法的主要参数为步长、截止标准、最大迭代次数、采样率.

2.1 迭代步长

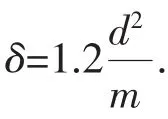
2.2 截止标准

SVT算法的截止标准为

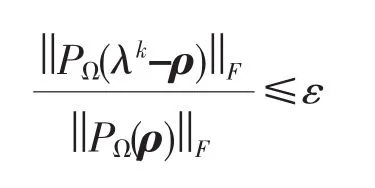
实验中，选取截止标准ε为1×10－4.

2.3 最大迭代次数

最大迭代次数表示为ρaxiter=500.

2.4 采样率

维数为d×d，采样数目为m，采样率定义为：

3 数值结果

泡利测量下的密度矩阵可通过cvx程序包编程进行数值模拟.cvx是用于解决非约束和带约束条件的凸优化问题，它是一种基于Matlab语言的建模系统.由于所研究的密度矩阵可用张量积直乘的形式表示，则用计算机代码容易实现.

本文的实验数据是在CPU：2 GHz；内存：2 GB的普通计算机上，使用Matlab软件程序模拟得到.利用SVT算法，通过在矩阵空间Ω上随机等分采样，得到如图1到图3的数值结果.

图1 不同采样率下的相对误差曲线图Fig.1 The relative error with sampling density in 6 qubits and 7qubits

通过对某一量子态下的密度矩阵相对误差的数值模拟和分析，得出重构效果良好的结论，在此基础上建模，能够很好地应用于量子态层析实验上，根据所建模型，在已知少量（不到一半）数据的情况下即可得到完整密度矩阵信息，且准确度较高.

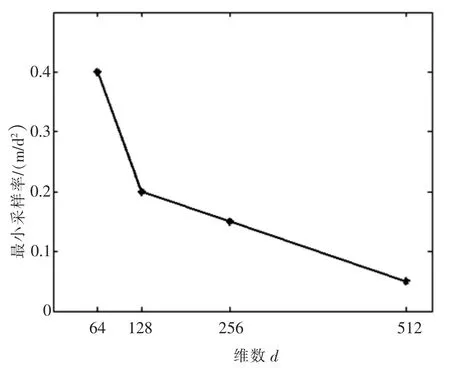
图2 不同维数下最小采样率变化图Fig.2 The relation of minimum sampling density with the size d

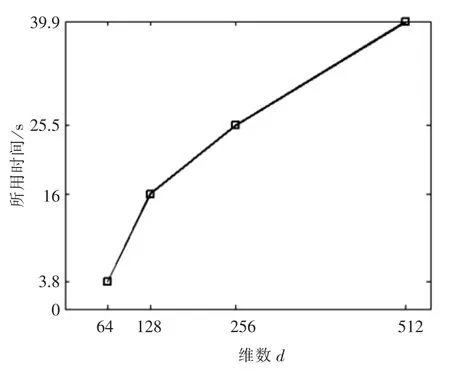
图3 不同维数下所用时间图Fig.3 The time required for SVT with the size d

为保证所建模型的可行性，本文除了评估重构矩阵的准确度外，还从最小采样率、所用时间方面进行讨论.最小采样率代表密度矩阵恰好实现重构时对应的采样数目与维数之比.一般认为，对于维数越大的矩阵，越需要从原始矩阵中采集较多的数据才能进行重构，但是由于密度矩阵的低秩性（即特征值的稀疏性），目标矩阵可通过特别少量的数据成功重构，且维数越大，需要的数据反而越少，这说明基于矩阵填充技术能够解决低秩大矩阵问题.

另外，原则上，维数越大的矩阵，模拟实验过程越耗时，但是随着采样率的降低，大大缩短了运行时间，这为研究更大量子比特下的密度矩阵问题提供参考基础.

4 结语

将近年来新兴的矩阵填充理论应用于重构泡利测量下未知密度矩阵中，用Matlab软件程序进行数值模拟，并且获得显著的重构效果，这为量子态层析提供了研究基础，对研究纯态或者近似纯态的量子体系具有一定意义.

致谢

本论文的研究是在硕士生课题方向的基础上开展的，感谢赵清教授、冯中营老师、康睿丹老师、王卫星老师对我的论文撰写和研究过程给予的帮助和指导.论文引用了数位学者的研究文献，在此一并表示感谢！

［1］MATTEO Paris，JAROSLAV Rehacek．Quantum state estimation［M］．Berlin:Springer Science＆Business Media，2004：1－8．

［2］戴宏毅．约化密度矩阵及其在量子信息处理中的应用［J］．大学物理，2010，29（2）：31－33．

DAI Hong－yi．Reduced density matrix and its application in quantum information processing［J］．College Physics，2010，29（2）：31－33．（in Chinese）

［3］DONOHO D L．Compressed sensing［J］．IEEE Transactions on Information Theory，2006，52（4）：1289－1306．

［4］胡端平，唐超．一致矩阵的特征性质［J］．武汉工程大学学报，2009，31（5）：93－94．

HU Duan－ping，TANG Chao．The character of consistent matrix［J］．Journal of Wuhan Institute of Technology，2009，31（5）：93－94．（in Chinese）

［5］杨建华，孙霞林．协方差矩阵在非负二次型估计中的可容许性［J］．武汉工程大学学报，2007，29（1）：75－77．

YANG Jian－hua，SUN Xia－lin．Compatibility of nonnegative quadractic estimation［J］．Journal of Wuhan Institute of Technology，2007，29（1）：75－77．（in Chinese）

［6］EMMANUEL J Candès，TERENCE Tao．The power of convex relaxation：Near－optimal matrix completion［J］．IEEE Transactions on Information Theory，2010，56（5）：2053－2080．

［7］CAI Jian－feng，EMMANUEL J Candes，SHEN Zuowei．A sngular value thresholding algorithm for matrix completion［J］．Siam Journal of Optimization，2010，20（4）：1956－1982．

［8］DAVE Gross．Recovering low－rank matrices from few coefficients in any basis［J］．IEEE Transactions on Information Theory，2011，57（3）：1548－1566．

Reconstructing low－rank density matrix via matrix completion

WEI Xian
Faculty of Science，Taiyuan Institute of Technology，Shanxi 030008，China

The problem of reconstructing low－rank or approximately low－rank matrix from the limited information is getting people＇s attention and solving this problem is well known as matrix completion．For the pure or nearly pure quantum state（ie．low entropy state）in a Hilbert space，the density matrix is low－rank and has trace 1．This paper is concerned with applying matrix completion theory to the unknown density matrix recovery which is from Pauli measurements．The singular value thresholding（SVT）algorithm was utilized to numerical simulation by Matlab software programs．And its soft－thresholding rule was used to singular values of the unknown state density matrix．The threshold iteration was conducted by SVT algorithm through computer programming until a stopping criteria was reached，which could greatly improve the run rate．We took the density matrix from Pauli measurements for example because of the convenience on getting the tensor product structure based on Pauli matrices in experiment．The effect of matrix reconstruction was studied in the case of sampling a small number of entries from the matrix．We conclude that the density matrix can be reconstructed successfully by studying the aspects of reconstruction error，run－time and sampling rate．

matrix completion；density matrix；low－rank；quantum state tomography

O413.1

A

10.3969/j.issn.1674-2869.2015.02.016

1674-2869（2015）02-0072-05

本文编辑：龚晓宁

2014－11－24

太原工业学院院级青年科学基金（2014LQ05）

韦仙（1988－），女，山西晋城人，助理实验师，硕士.研究方向：理论物理.