有效试验数据对钢材机械性能分布规律的影响

李清，袁小会，刘岑，吴元祥，刘兵，刘小宁，*

1.武汉软件工程职业学院机械工程学院，湖北 武汉 430205；2.武汉工程大学机电工程学院，湖北 武汉 430205

有效试验数据对钢材机械性能分布规律的影响

李清1，袁小会1，刘岑2，吴元祥1，刘兵1，刘小宁1，2*

1.武汉软件工程职业学院机械工程学院，湖北 武汉 430205；2.武汉工程大学机电工程学院，湖北 武汉 430205

为了建立机械强度可靠性设计方法，必须分析钢材抗拉强度与屈服强度的分布规律；判别抗拉强度与屈服强度试验数据的有效性是研究其分布规律的基础.应用数理统计理论，建立了试验数据有效性的判别方法.基于9%预应变奥氏体不锈钢S30408在液氮温度下的抗拉强度与屈服强度试验数据，在单侧置信度为99%时，判别了试验数据的有效性；根据有效试验数据与可靠性理论，对钢材抗拉强度与屈服强度的分布规律进行了假设检验.研究表明：试验数据的有效性对分布规律的影响不可忽视；在显著度为0．05时，抗拉强度基本符合正态分布，屈服强度似不符合正态分布.

抗拉强度；屈服强度；试验数据；有效性；分布规律；S30408钢；9%预应变

0 引言

抗拉强度与屈服强度是钢材机械性能的重要指标，基于试验数据，分析与探索抗拉强度与屈服强度的分布规律，是建立机械强度可靠性设计方法的内容之一［1－7］.

获得比较多的试验数据是分析与探索抗拉强度与屈服强度分布规律的前提，由于试验的影响因素比较多，试验数据比较分散［8－9］，必须对试验数据的有效性进行判别，剔除因意外因素影响而形成的无效数据；因此，如何判别试验数据的有效性，是分析与探索分布规律的基础.文献［1］认为，当试验数据比较少时，可将钢材的抗拉与屈服强度视作正态分布；随着科学技术的进步，钢材试验数据的增加，对抗拉强度与屈服强度分布规律进行分析成为可能.

文中应用数理统计理论［1，10－11］，建立了试验数据有效性的判别方法，基于9%预应变奥氏体不锈钢S30408在液氮温度下的有效试验数据，研究了其抗拉强度与屈服强度的分布规律.

1 理论分析

工程上采用有限的试验数据分析钢材抗拉强度与屈服强度的分布规律，如果通过试验测量得到抗拉与屈服强度的n组试验数据Ri（i＝1，2，…，n），不难得到试验数据的准确度与精密度［10－11］：

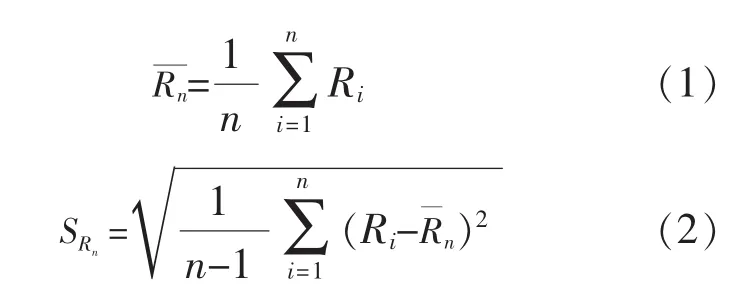
1.1 试验数据有效性的判别方法

单侧置信度为（1～0．5α）时，由试验数据组数n和t分布性质，可确定t分布系数tn－1，1－0．5α，作为试验数据有效性的判别依据，文中所用的t分布系数如表1所示［11］.

表1 t与χ2系数Table 1 Coefficient t andχ2

试验数据Ri有效性的判别指标为［9］：

如果

则表明Ri不是有效试验数据，需要剔除；剔除无效数据应从试验数据的最大或者最小值开始，每剔除1个无效数据，都要计算其余数据的准确度与精密度，再进行有效性判别；若存在r个无效数据，则最后对（n－r）个有效数据需要重新计算其准确度与精密度.

工程上认为小概率事件在一次试验中是不可能发生的，因此可取α＝0．10，0．05，0．02，本文取α＝0．02，即在单侧置信度为99%时，分析试验数据的有效性，表明有99%把握认为剔除的数据是意外因素影响而形成的无效数据.

1.2 分布规律的假设检验

在试验数据比较少时，可将钢材抗拉强度与屈服强度视为基本符合正态分布的随机变量［1］；随着试验数据的增加，对抗拉强度与屈服强度分布规律进行假设检验成为可能，其具体方法是［1，11］：

（1）假设.即假设钢材抗拉强度与屈服强度基本符合正态分布.

（2）分组.根据有效试验数据个数（n－r），把有效试验数据R1、R2、…、Rn－r分为M个区间，M＝1＋3．3lg（n－r），并取整数.

（3）计算理论频数.对于符合正态分布的随机变量R，其统计量Ri落在分组区间［a1，a2］，［a2，a3］，…，［aM，aM＋1］内的理论概率为

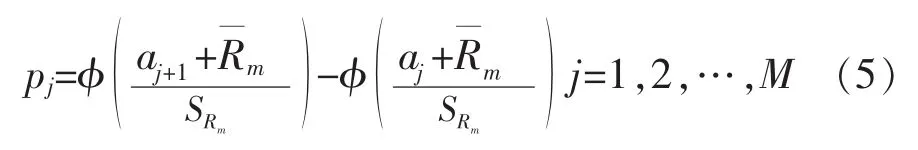
式（5）中，Φ（·）为标准正态积分；a1＝（Ri）min，aM＋1＝（Ri）max，（Ri）min、（Ri）max分别为Ri中的最小值与最大值.

其中

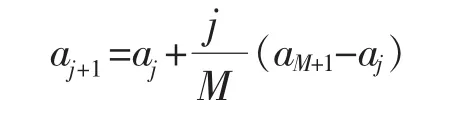
对于（n－r）个有效试验数据，其统计量Ri落在分组区间［aj，aj＋1］内的理论频数为（n－r）×pj.

（4）计算皮尔逊统计量之和.即计算每个分组区间实际频数（Nj）与理论频数（m－n）×pj差异的皮尔逊统计量之和，即计算：

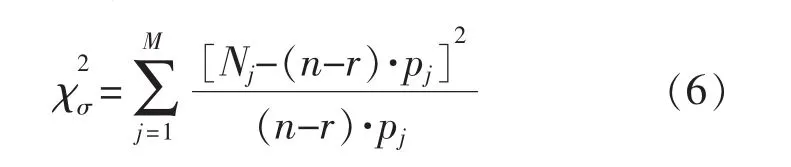
工程上一般取显著度δ＝0．05，文中所用的系数见表1［1，11］.

2 分布规律的假设检验

2.1 试验数据的有效性判别

奥氏体不锈钢S30408是制造深冷容器的常用钢材之一，在液氮温度下，文献［8］获得了9%预应变S30408钢抗拉强度与屈服强度的43组试验数据，由小至大的排序如表2所示.

表2 9%预应变S30408钢抗拉与屈服强度的43组试验数据Table 2 43 Sets test data of tensile and yield strength of 9%-prestrained steel S30408 MPa

将表2的试验数据代入式（1）与式（2），可分别得到43组抗拉与屈服强度的准确度与精密度，如表3所示.

由式（3）与式（4）可知第43组抗拉强度试验数据Rm43＝1 785 MPa的|t43|＝2．436＞t42，0．99＝2．420，因此，该数据是无效的.余下的42组试验数据重新统计，得到的统计数据列入表3；再一次用式（3）与式（4）可知，第42组Rm42＝1 784 MPa抗拉强度试验数据的|t42|＝2．640＞t41，0．99＝2．421，因此，该数据也是无效的；其他41组试验数据的统计参数列入表3，经用式（3）与式（4）判别，41组试验数据的| ti|＜t40，0．99＝2．423，表明都是有效的.

用类似的方法，可知表2中屈服强度试验数据第1组ReL1＝409 MPa的|t1|＝2．787＞t42，0．99＝2．420，因此，该数据是无效的，需要剔除；其余42组试验数据的统计参数列入表3，经用式（3）与式（4）判别，其余42组试验数据的|ti|＜t41，0．99＝2．421，表明其余试验数据均有效.

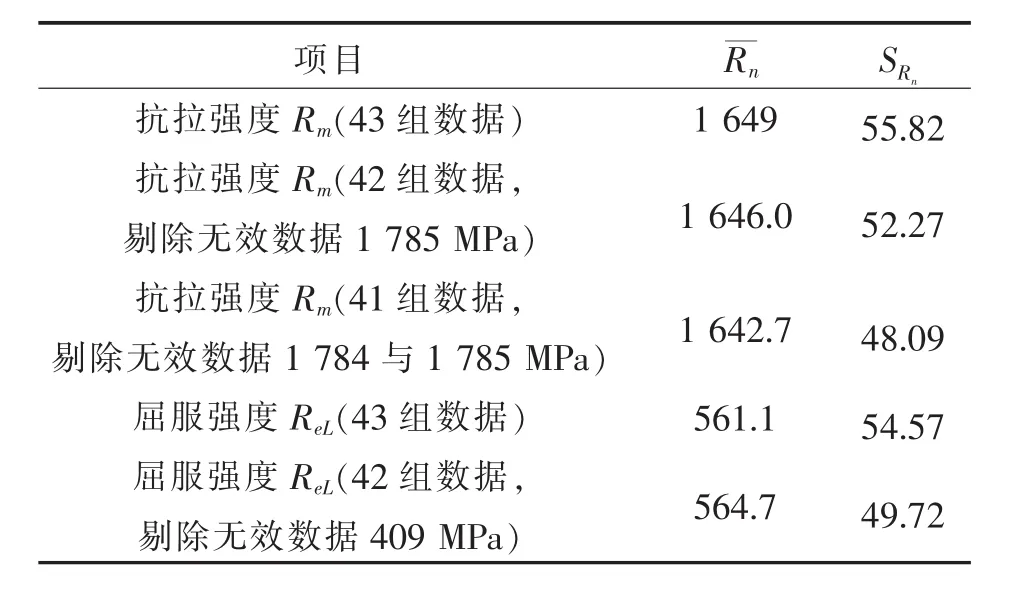
表3 试验数据的统计Table 3 Test data statistics MPa

2.2 抗拉强度分布规律的假设检验

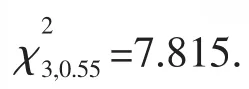
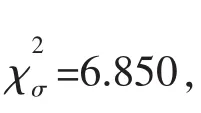
表4 抗拉强度的皮尔逊统计量χ2（41组有效试验数据）Table 4 Statisticχ2of tensile strength（41 sets validity test data）

3 讨论

3.1 试验数据有效性对分布规律分析的影响

如果不考虑试验数据的有效性，按上述方法计算43组抗拉强度试验数据的皮尔逊统计量之和，如表5所示.

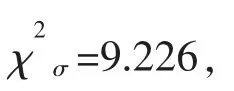
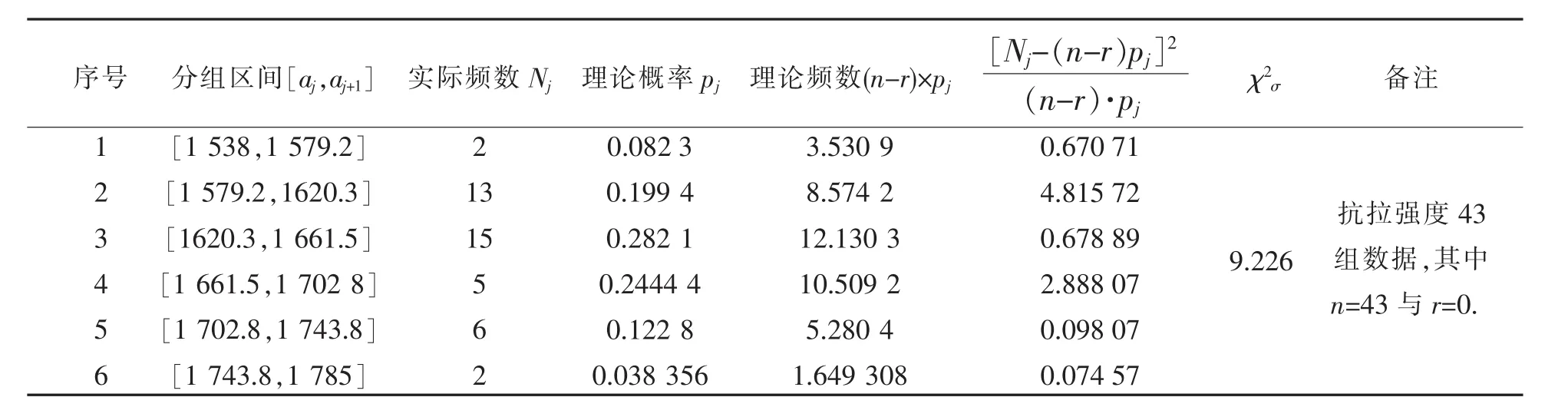
表5 抗拉强度的皮尔逊统计量χ2（43组试验数据）Table 5 Statisticχ2of tensile strength（43 sets test data）

根据以上讨论可知，应用数理统计理论，分析试验数据的有效性，是分析抗拉强度分布规律的基础，如果不剔除无效数据，可能得到不正确的结论.

3.2 屈服强度分布规律的讨论

在液氮温度下，9%预应变奥氏体不锈钢S30408屈服强度的分布规律，也可采用假设检验方法进行分析.

假设屈服强度基本符合正态分布，基于42组有效试验数据，可得到屈服强度的皮尔逊统计量，如表6所示.

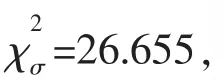
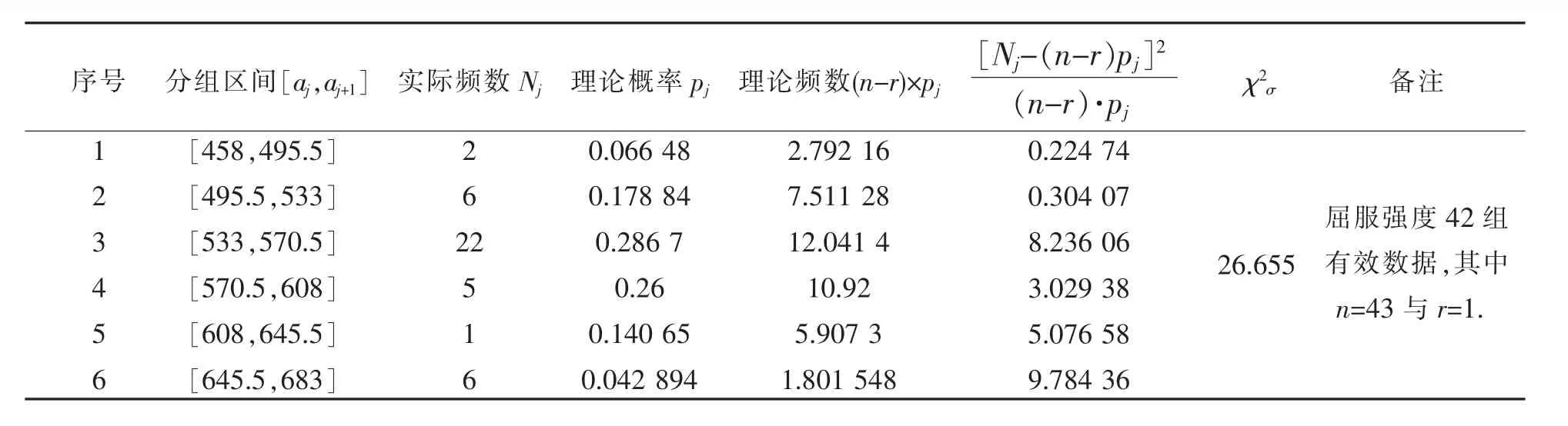
表6 屈服强度的皮尔逊统计量（42组有效试验数据）Table 6 Statisticof yield strength(42 sets validity test data)

以上分析表明，奥氏体不锈钢S30408抗拉强度与屈服强度的分布规律可能存在不一致.

另外，文献［8-9］利用所有试验数据，分析奥氏体不锈钢S30408抗拉强度与屈服强度的分布规律与分布参数，没有剔除无效数据似不妥.

4 结语

a.试验数据的有效性对钢材机械性能分布规律的研究影响比较大，如果不剔除无效数据，可能得到不正确的结论；文中建立了试验数据有效性的分析方法，在单侧置信度为99%时，分析了有关试验数据的有效性.

b.在显著度为0．05时，9%预应变奥氏体不锈钢S30408在液氮温度下的抗拉强度，是基本符合正态分布的随机变量，但其屈服强度似不符合正态分布.

c.建立机械强度的可靠性设计方法，必须重视钢材抗拉强度与屈服强度分布规律可能存在的不一致.

致谢

感谢湖北省教育厅科研项目（B2014209）对本研究的资助！

［1］徐灏．机械强度的可靠性设计［M］．北京：机械工业出版社，1984．

XU Hao．Mechanical strength reliability design［M］．Beijing：Mechanical Industry Publishing House，1984．（in Chinese）

［2］袁小会，刘岑，吴元祥，等．单层厚壁圆筒容器爆破压力的分布规律与参数［J］．武汉工程大学学报，2014，36（2）：49－55．

YUAN Xiao－hui，LIU Cen，WU Yuan－xiang，et al． Distribution law and parameters of monolayer thickwall cylindrical vessel burst pressure［J］．Journal of Wuhan Institute of Technology，2014，36（2）：49－55．（in Chinese）

［3］刘小宁，刘岑，张红卫，等．球形容器静强度的分布规律与参数［J］．压力容器，2012，29（8）：26－30．

LIU Xiao－ning，LIU Cen，ZHANG Hong－wei，et al．New methods of calculation distribution law and parameters of the spherical vessel static strength［J］．Pressure Vessel Technology，2012，29（8）：26－30．（in Chinese）

［4］刘小宁．基于许用可靠度的超高压圆筒爆破安全系数［J］．制造业自动化，2015，37（2）：73－75．

LIU Xiao－ning．Burst safety factor of super－high pressure cylinder based on allowable reliability［J］．Manufacturing Automation，2015，37（2）：73－75．（in Chinese）

［5］刘小宁，张红卫，刘岑，等．钢制薄壁内压容器静强度的可靠性设计［J］．工业安全与环保，2011，37（3）：48－50．

LIU Xiao－ning，ZHANG Hong－wei，LIU Cen，et al．Reliability design of static strength for steel thin wall ento－pressure vessel［J］．Industrial Safety and Environmental Protection，2011，37（3）：48－50．（in Chinese）

［6］刘小宁，刘岑，刘兵，等．密封螺栓的模糊许用可靠度与安全系数［J］．现代制造工程，2014（10）：134－137．

LIU Xiao－ning，LIU Cen，LIU Bing，et al．Safety factor of seal bolt based on fuzzy allowable reliability［J］．Modern Manufacturing Engineering，2014（10）：134－137．（in Chinese）

［7］刘小宁，张红卫，韩春鸣．基于模糊可靠度的薄壁外压容器稳定性设计［J］．机械强度，2011，33（2）：217－224．

LIU Xiao－ning，ZHANG Hong－wei，HAN Chun－ming．Stability design of steel thin wall external pressure vessels based on fuzzy reliability［J］．Journal of Mechanical Strength，2011，33（2）：217－224．（in Chinese）

［8］郑津洋，王珂，黄泽，等．液氮温度下奥氏体不锈钢强度试验研究［J］．压力容器，2014，31（8）：1－6．

ZHENG Jin－yang，WANG Ke,HUANG Ze，et al．Study on strength of austenite stainless steel under liquid－nitrogen temperature［J］．Pressure Vessel Technology，2014，31（8）：1－6．（in Chinese）

［9］黄泽，缪存坚，李涛，等．预拉伸奥氏体不锈钢常温拉伸力学性能试验研究［J］．压力容器，2013，30（6）：7－11．

HUANG Ze，MIAO Cun－jian，LI Tao，et al．Experimental study on tensile mechanical properties of prestrained austenitic stainless steel at normal atmospheric temperature［J］．Pressure Vessel Technology，2013，30（6）：7－11．（in Chinese）

［10］刘智敏．误差与数据处理［M］．北京：原子能出版社，1981．

LIU Zhi－min．Errors and data processing［M］．Beijing：Atomic Energy Press，1981．（in Chinese）

［11］化学工程手册编辑委员会．化工应用数学［M］．北京：化学工业出版社，1983：23－28，369－375．

Editorial Board of Chemical Engineering Handbook．Chemical application mathematics［M］．Beijing：Chemical Industry Press，1983：23－28，369－375．（in Chinese）

Validity test data effect on steel mechanical properties distribution law

LI Qing1，YUAN Xiao－hui1，LIU Cen2，WU Yuan－xiang1，LIU Bing1，LIU Xiao－ning1，2*
1.School of Mechanical Engineering，Wuhan Polytechnic College of Software and Engineering，Wuhan 430205，China；2.School of Mechanical and Electrical Engineering，Wuhan Institute of Technology，Wuhan 430205，China

To establish mechanical strength reliability design method，the tensile strength and yield strength of the steel distribution law must be analyzed；distinguishing the test data validity of steel tensile strength and yield strength is the basis of studying distribution law．Applying mathematical statistics theory，the method for judging the validity of test data was established．Based on tensile strength and yield strength test data of 9%－prestrained austenite stainless steel S30408 at liquid nitrogen temperature，the test data validity was judged at one－sided confidence of 99%；the distribution law of the steel tensile strength and yield strength was studied by hypothetical test based on the validity test data and reliability theory．Results show that the influence of the validity of test data on the distribution law cannot be ignored；at the saliency of 0．05，the tensile strength is random variable which conforms to normal distribution while the yield strength seems not consistent with the normal distribution．

tensile strength；yield strength；test data；validity；distribution law；steel S30408；9%－prestrained

TH 49 O213.2

A

10.3969/j.issn.1674-2869.2015.04.015

1674-2869（2015）04-0069-05

本文编辑：陈小平

2015－03－02

湖北省教育厅科研项目（B2014209）

李清（1965－），女，湖北武汉人，副教授.研究方向：机械设计与制造等.*通信联系人.