蒙特卡罗方法在金融衍生品定价上的应用

洪铁松

(上海财经大学浙江学院，浙江 金华 321000)

20世纪70年代初，布莱克(Fisher Black)、斯科尔斯(Myron Scholes)和默顿(Robert Merton)取得股票期权定价问题上的一个突破。他们的成果就是在金融工程上具有里程碑意义的 Black－Schloles(或 Black－Schloles－Merton)模型。随后在这基础上有更多更复杂的模型，被开发出来用于金融衍生品价格的计算。譬如局部波动率模型(local volatility model)、概率波动率模型(stochastic volatility model)、跳跃模型(jump model)等。但当资产价格变动的概率过程为复杂模型时，其求衍生品价格的解析解的难度就大幅上升。不仅如此，对于一些有着复杂的损益计算函数或者收益依附于标的证券的历史数据(路径依赖型)的奇异期权等金融衍生品来说，至今人们还没得出定价的解析解。于是，随之产生的就是使用各种数值方法来对衍生品进行定价。随着计算机技术的快速发展，数值计算方法之一的蒙特卡罗方法逐渐成为使用最方便最广泛的衍生品定价方法。

一、布莱克－斯科尔斯期权定价模型

(一)模型的基本假设

在对股票期权等金融衍生品进行定价的时候，使用最多最有名的股票价格波动模型是布莱克－斯科尔斯模型(Black－Scholes Model)，在其模型当中股票价格假定为服从以下的几何布朗运动:

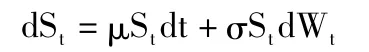
(二)风险中性定价

虽然假定股票价格在市场测度P下的概率微分方程式为dSt=μStdt+σStdWt，但是在求期权价格的时候，根据无套利原则，B－S微分方程独立于风险偏好，也就是不管原资产的漂移率为多少，最终都变为无风险利率。这就是我们所说的风险中性概率测度Q(鞅测度)，在该测度下，资产的价格变动概率微分方程式为dSt=rStdt+σStdWt。如果期权到期时的价值为XT=f(ST)，那么它在今天的价值就是在风险中性概率测度下的期望值的现值X0=e－rTEQ［f(ST)］。譬如欧式看涨期权到期时的价值为max{ST－K，0}，其在目前的价值就是 e－rTEQ［max{ST－K，0}］。

二、蒙特卡罗模拟方法

蒙特卡罗方法是使用随机数进行数值计算的总称。在金融领域的实际应用上，蒙特卡罗方法的主要思想就是:反复使用随机数进行数值实验，从大量的实验结果当中求解目标因素。该方法的基本思想就是:首先，使用随机数表现概率事件(标的资产的价格变化等)。其次，把生成的随机数带入概率变量(金融衍生品的价值等)计算实现值。最后，对概率变量的实现值进行集合处理。

在使用蒙特卡洛法计算期权的价格时，其基本方法是:生成随机数模拟产生标的资产的随机价格样本，计算出到期时期权的价值，反复上述步骤，最后以期权价值的平均现值作为该期权的价格。下面给出在Excel VBA上用蒙特卡洛模拟方法实现期权价值计算的过程:

1.生成服从均匀分布的随机数。使用Excel工作表函数rand()或VBA函数rnd()就能生成服从均匀分布U(0，1)的随机数。

2.把服从均匀分布的随机数转换为服从标准正态分布的随机数。在使用Excel生成标准正态随机数时，可以把第一步生成的U(0，1)随机数代入标准正态分布的逆函数NormSInv()来生成，但这样的方法需要耗费大量的计算时间。通常我们可以使用Box－Muller法或Moro法更加快速的生成服从标准正态分布的随机数。

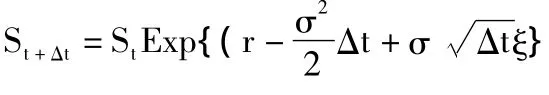
对上述过程进行必要次数的重复，生成大量的风险中性测度下期权价值的样本值;

4.计算出所有样本的期权价值的平均值;用无风险利率折算出期权价值平均值的现在价值就为该期权价格的推测值。

三、应用案例分析

欧式或美式看涨期权和看跌期权这样的衍生品被称为标准型产品，通常人们可以在交易所里集中进行交易。除此之外，在场外市场上还存在许多的非标准化产品，人们把它们称之为奇异期权(Exotic Option)，这类期权的定价过程相对比较复杂，即使存在解析解，也往往与现实存在一定的偏差。回望期权(Lookback Option)就是其中一类奇异期权，它最终的损益依赖于标的资产的价格路径。回望看涨期权定义为持有者能够以期权有效期内所能达到的最低价格购买标的资产。同样的，回望看跌期权的持有者能够以期权有效期内所能达到的最高价格出售标的资产。

例:考虑一个新发行的基于不支付红利股票的回望看涨期权，股票当前的价格S_0为50，股票价格的波动率σ为40%，无风险利率r为10%，到期期限T为3个月。

欧式回望期权在连续模型下存在解析解，该看涨期权的价值为8.04。使用蒙特卡罗方法模拟计算该期权价格的过程中，我们需要在风险中性测度下模拟出股票路径，设置价格观测点，并对同一路径不同观测点上的股票价格进行对比，得出最低股价作为行使价格，从而计算出期权的到期损益Max{ST－Smin，0}。下面为使用蒙特卡罗方法在 Excel VBA上编辑用户定义函数对回望看涨期权进行数值求解的程序代码:

主函数当中用到了使用Box－Muller法生成服从标准正态分布随机数的Excel VBA用户定义函数，其具体的代码如下:

在这里，我们对到期时间进行了分割(价格观测点分为100次和1000次)，以观测各个时点上的股票价格。具体的模拟计算结果如下:

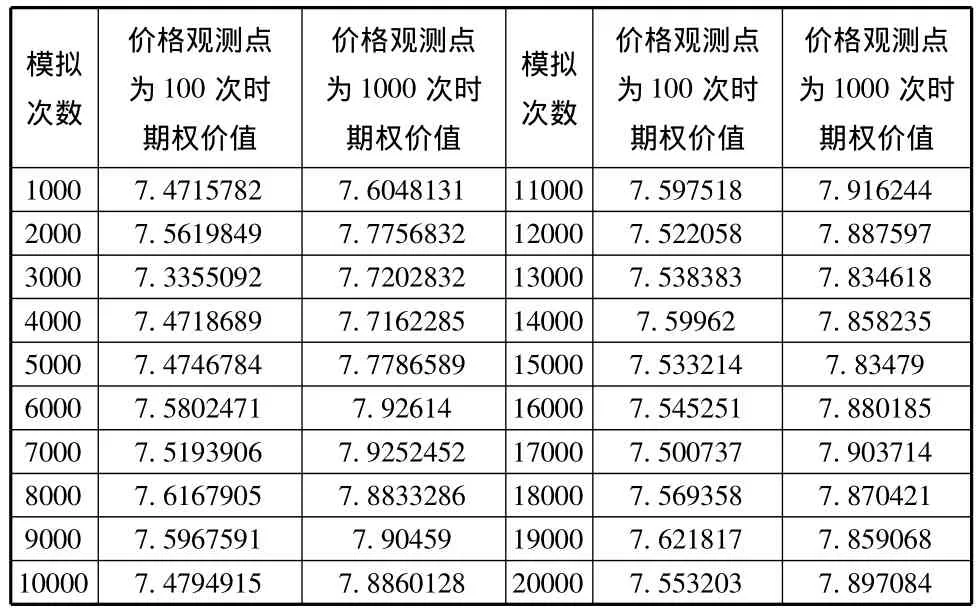
表1 蒙特卡罗模拟计算结果

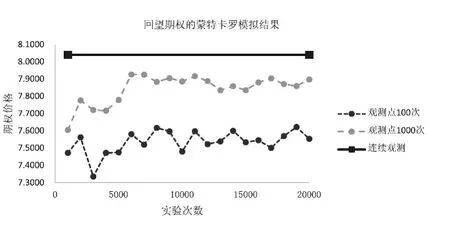
图1 期权价值的收敛过程

回望期权的价值取决于期权有效期内能够观测到的标的资产的最低价格或最高价格。连续模型下回望期权的定价存在解析解，这意味着在期权的有效期内，标的资产的价格能够连续的进行观测并从中得出最低价格和最高价格。但在现实中，对于标的资产的价格观测是离散的(譬如每日收盘价格)。由此，连续模型下的定价解析解无非只能看作是现实价格的近似解。一般，随着观测频率的增加，也就是观测时间的缩短，观测到更高的最高价和更低的最低价的可能性也随之上升。因此，回望期权的价格会随观测频率的上升而上升。

四、总结

对金融衍生品的定价除了使用蒙特卡洛模拟运算之外，还有解析解的导出、有限差分法以及使用二叉树数值计算等各种方法。但是，很多时候从股价模型往往无法导出解析解。在对奇异期权等一些路径依存型的衍生产品进行定价的时候，原则上只得使用蒙特卡洛数值计算方法。随着计算机技术的不断发展，今天我们可以使用最常用的办公软件来对金融衍生品的定价进行数值计算。正是因为蒙特卡罗方法在实施上简易可行，在大学里可用于金融工程的辅助教学，在金融实务应用上也有很大的发展空间。事实上，使用蒙特卡洛法对期权进行定价计算越来越得到重视，同时提高计算效率的各种技术的开发与应用也在不断地得到深化和推广。

［1］Black，F.，Scholes，M.1973.“The pricing of options and corporate liabilities”，Journal of Political Economic 81，637－654.

［2］ Boyle，P.P.，1977，“Options:A Monte Carlo Approach，”Journal of Finacial Economics，4:323－38.

［3］徐永春，2013，《蒙特卡罗方法下的期权类衍生产品定价》，《统计与决策》第15期，第161－163页.

［4］约翰·赫尔，2010，《期权、期货及其他衍生产品》，北京:人们邮电出版社.

［5］西蒙·本尼卡，2010，《财务金融建模——用Excel工具(第三版)》，上海:上海人民出版社.