基于Matlab的共轭凸轮机构设计

魏 奔， 孙志宏， 李子军

(1. 东华大学 a. 机械工程学院；b. 纺织装备教育部工程研究中心，上海201620；2. 山东日发纺织机械有限公司，山东 聊城252000)

基于Matlab的共轭凸轮机构设计

魏 奔1a, 1b， 孙志宏1a, 1b， 李子军2

(1. 东华大学 a. 机械工程学院；b. 纺织装备教育部工程研究中心，上海201620；2. 山东日发纺织机械有限公司，山东 聊城252000)

以满足机构许用压力角为约束条件，利用Matlab开发了一款共轭凸轮辅助设计软件，可视化求解共轭凸轮转动中心的可行域，通过人机交互在可行域内选定凸轮转动中心位置，自动生成主、副凸轮的廓线及其特征点数据，极大提高了共轭凸轮的设计效率. Matlab软件生成的数据文件可直接用于数控加工，具有重要的实际应用价值.

共轭凸轮； 压力角； 凸轮转动中心可行域； Matlab

共轭凸轮机构中，只要设计出适当的主、副凸轮的廓线，就能够精确地控制从动件作各种预期的往复运动，因此，共轭凸轮机构被广泛应用于轻工、纺织、食品等领域[1].

目前，已有的共轭凸轮机构计算机辅助设计软件的基本原理为：给定共轭凸轮结构参数，通过理论分析获得共轭凸轮的理论廓线方程及实际廓线方程，借助计算机的计算与绘图功能，生成共轭凸轮廓线以及凸轮廓线上特征点，指导生产加工.但在设计之初，通常并不能事先知道凸轮机构基本结构参数(现多为测绘国外设备获得)，现有凸轮辅助设计软件也无法进行结构参数设计.本文在已知共轭凸轮机构从动件运动规律和许用压力角α的条件下，计算出凸轮转动中心的可行域，并通过计算机可视化显示，人机交互选定其位置后，计算机自动生成凸轮的理论廓线和工作廓线，该软件将有助于设计人员进行共轭凸轮机构的原创设计.

1 从动件运动规律

在设计凸轮机构基本尺寸和凸轮轮廓之前，必须根据凸轮机构的工作性能要求建立从动件运动规律方程式.从动件的运动规律将直接影响凸轮机构的基本尺寸设计、轮廓设计和凸轮机构的运动性能.从动件运动规律可分为基本运动规律和组合运动规律，组合运动规律是由数种基本运动规律拼接而成[2].运动规律的拼接原则是各段基本运动规律在衔接点上的运动参数(如位移、类速度、类加速度，有时还包括类跃度)保持连续，在运动的起始点和终止点上的运动参数满足边界条件[3-8]，限于篇幅，本文不作详细介绍.

2 设计思路与方法

2.1 基于许用压力角的凸轮转动中心设置区求解

2.1.1 压力角与凸轮转动中心位置的关系

压力角与凸轮轴位置关系如图1所示.

(a) P12在O1O2连线上 (b) P12在O1O2延长线上

图1中，O1为凸轮转动中心，O2为从动件的摆动中心.设凸轮、从动摆杆和机架分别为构件1、 2、 3，易知构件1、 3瞬心P13和构件2、 3瞬心P23.A点为摆杆O2A上滚子转动中心，α为O2A杆运动到此时刻机构压力角，力F2、F1分别为凸轮和滚子中心的作用力与反作用力，方向沿滚子中心与凸轮理论廓线接触点的法线方向，沿此方向作AP12与O1O2(或其延长线)交于点P12，由三心定理可知，点P12即为构件1、 2的瞬心.v2为滚子中心A点的线速度，方向垂直摆杆O2A.自O1作O1B∥AP12，与O2A(或其延长线)交于B点，已知凸轮与从动杆角速度分别为ω1、ω2，假设不考虑摩擦力，由机械原理可知，当ω1、ω2反向时，瞬心P12落在O1O2连线上(图1(a))，而当ω1、ω2同向时，瞬心P12落在O1O2延长线上(图1(b))，因此，均有：

ω2·P23P12=-ω1·P12P13

(1)

(2)

根据以上所述，可得以下结论.

(1) AB线段长度等于从动杆上滚子转动中心线速度与凸轮角速度的比值(以下简称速比).

(2) 若给定凸轮机构许用压力角为α，在机构运动某一时刻，自A点在O2A或O2A的延长线上截取线段AB，使其大小等于上述瞬时速比，得B点.再自B点作两直线，使其与O2A杆分别成90°-α和90°+α(称为界线直线)，如图2所示.则在此两直线所夹区域内(包括两界线直线)，凸轮压力角将小于等于许用压力角α，此区域即为该时刻对应的凸轮转动中心设置区.将凸轮机构运动一个周期内各时刻所对应的两根界线直线绘出，这一系列界线直线所包围的共有区域，即为在凸轮运动全周期内满足许用压力角要求的凸轮转动中心设置区(以下简称可行域).

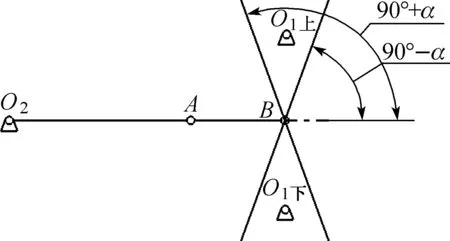
图2 凸轮转动中心设置区边界线示意图Fig.2 The boundary lines of cam shaft’s feasible region

(3) 如图2所示，若凸轮转动中心O1设置在摆杆O2A的下方，则界线直线取下半部分(O1 下所在区域)，反之，若凸轮转动中心O1设置在摆杆O2A的上方，则界线直线取上半部分(O1上所在区域).

(4) 由于共轭凸轮机构中主从动杆与副从动杆固结在一起，其运动规律完全相同，因此，通过上述方法所绘出的主、副凸轮转动中心可行域图形上完全一致.如图3(a)所示，左一与右一区域内线条族所夹区域为主凸轮可行域，左二与右二区域内线条族所夹区域为副凸轮可行域.图3(a)中右二与左二区域内线条族分别为左一与右一区域内线条族绕中心O2顺时针旋转γ角所得.只画出4个曲线族的包络线如图3(b)所示，结合图3(a)和3(b)可知，求解共轭凸轮转动中心可行域时，只需绘制主凸轮可行域边界直线族所围区域，即图3(b)中曲线1、 4和曲线2、 3所围区域，再将曲线2、 3绕O2点顺时针旋转γ角(主、副从动杆夹角)得曲线2′、3′，2′、3′两曲线所围区域即为副凸轮转动中心的可行域.两边界直线族所围共有区域(图3(c)中阴影区域)即为满足许用压力角要求的共轭凸轮转动中心可行域.下面将介绍图3(c)中4条曲线求解方法.

(a) 凸轮可行域求解原理图

(b) 凸轮可行域简化示意图

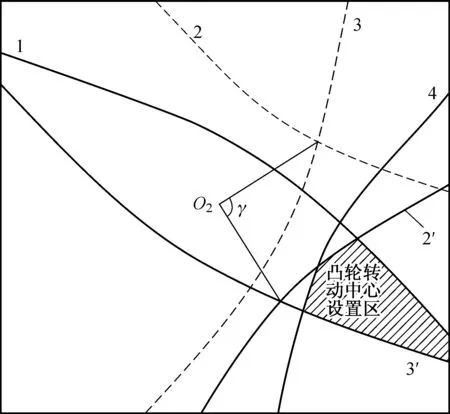
(c) 解析法求解凸轮可行域示意图

2.1.2 基于许用压力角的凸轮转动中心可行域求解

图3(b)中4条曲线实为图3(a)中左一与右一区域内边界直线族所构成的包络线，下面引入直线族包络线的数学表达式.

(a) B点落在O2A延长线上

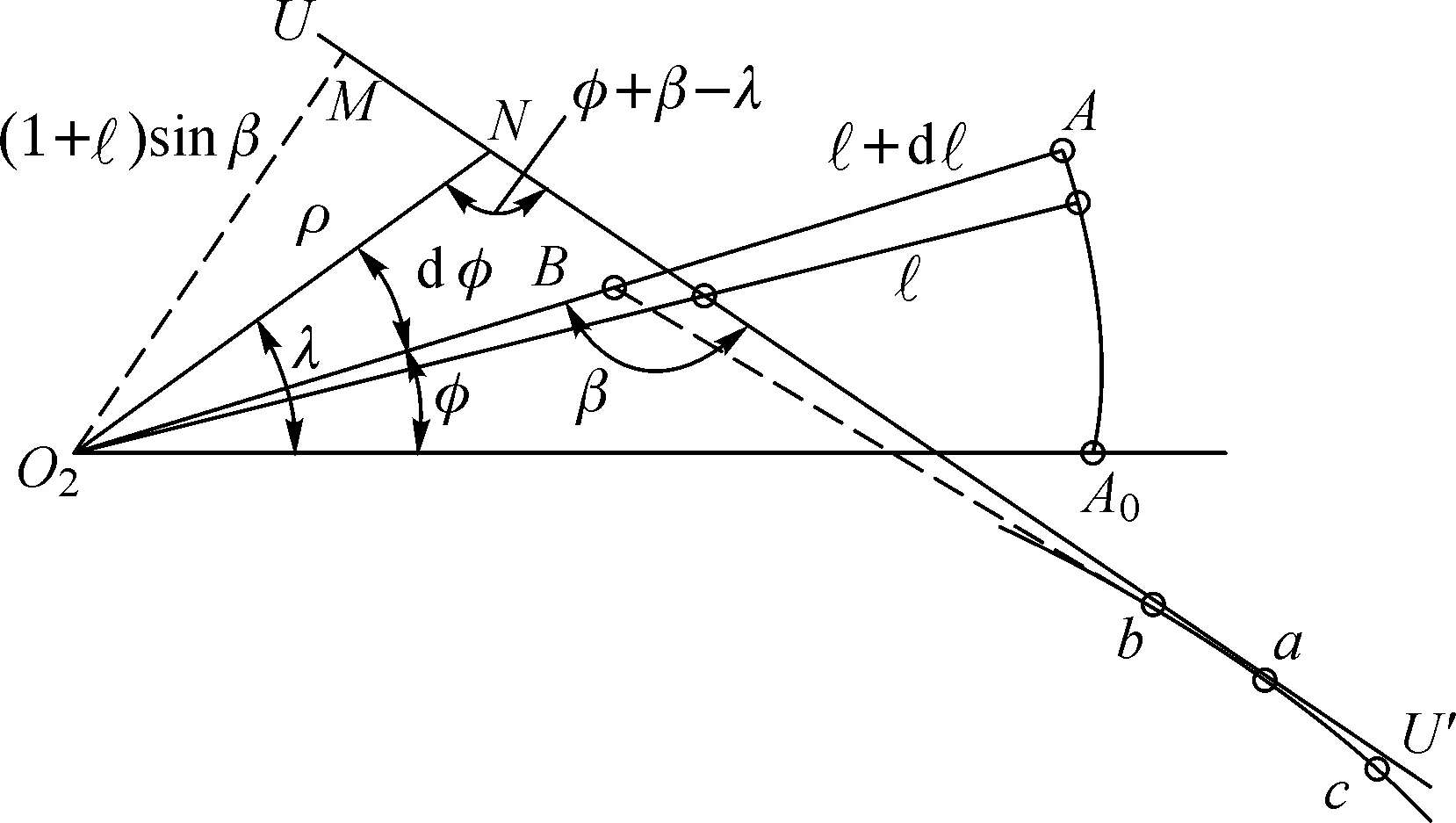
(b) B点落在O2A上

如图4所示，O2点为极坐标的极点，从动杆起始位置O2A0为极轴.设从动杆任意位置O2A摆角为φ，此时界线为UU′，N为此直线上任意一点，该点的向径为ρ，极角为λ.取O2A=1，AB=作O2M⊥UU′，则

O2M=(1+)sinβ

在△O2MN中，UU′方程为

ρsin(φ+β-λ)=(1+)sinβ

(3)

无限接近直线方程为

ρsin(φ′+β-λ)=(1+′)sinβ

(4)

式中：φ′=φ+dφ，′=+d.

由式(3)减式(4)得：

(5)

联立式(3)～(5)求得可行域边界包络线方程式为

(6)

(7)

式中：ε2为从动件角加速度；β取90°-α或90°+α(选取规则在后文进行讨论).将推程和回程从动件运动参数(即角位移φ、角速度ω2和角加速度ε2)代入式(6)和(7)，即可求得极坐标下凸轮转动中心可行域.式(6)和(7)使用时应注意以下几个问题.

(1) 在推程或回程起始(φb)和终止时刻(φe)ω2为零，式(6)中，因sinβ不为零，ρ将取无穷大，考虑到计算机绘图高效性，令计算起始时刻为φb+ξ(ξ>0， 大小可调整)，终止时刻为φe-ξ，避免sinβ为零；

(2) 当从动件运动规律为等速运动时，因从动件角速度ω2保持不变，又凸轮角速度ω1恒定，式(6)中β不变，可求得ρ为常量，所以所求得4条包络线为4段以O2为圆心的圆弧，不能求得凸轮转动中心可行域.调整包络线求解方程组为：式(3)和(7)，计算时先通过式(7)求得λ，再代入式(3)求得ρ，此问题得到解决.

(3) 通过式(6)和(7)或式(3)和(7)计算图3(c)中4条包络线时β的取值见表1所示.

(4) 图3(c)中曲线2、3是由图3(b)中曲线2、3顺时针旋转γ角获得，因此，实际计算时ε应取ε-γ.

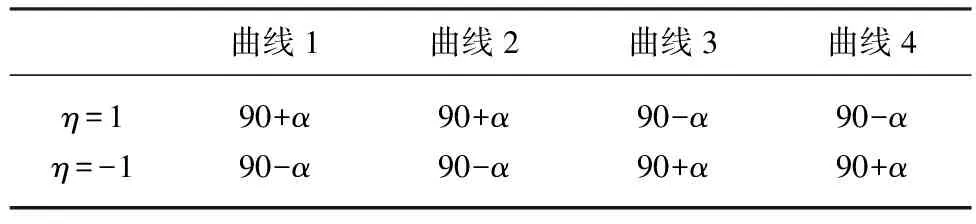
表1 β取值表

注：当凸轮转向与从动件推程运动方向相同时η=1，反之，η=-1.

2.2 共轭凸轮廓线方程推导

如图5所示，取凸轮转动中心O1为原点建立直角坐标系. 图5中, 从动杆O2B起始角为φ0；凸轮转动中心到从动件转动中心的中心距为a；从动件杆长为，主、副从动杆夹角为γ；凸轮以ω逆时针旋转.

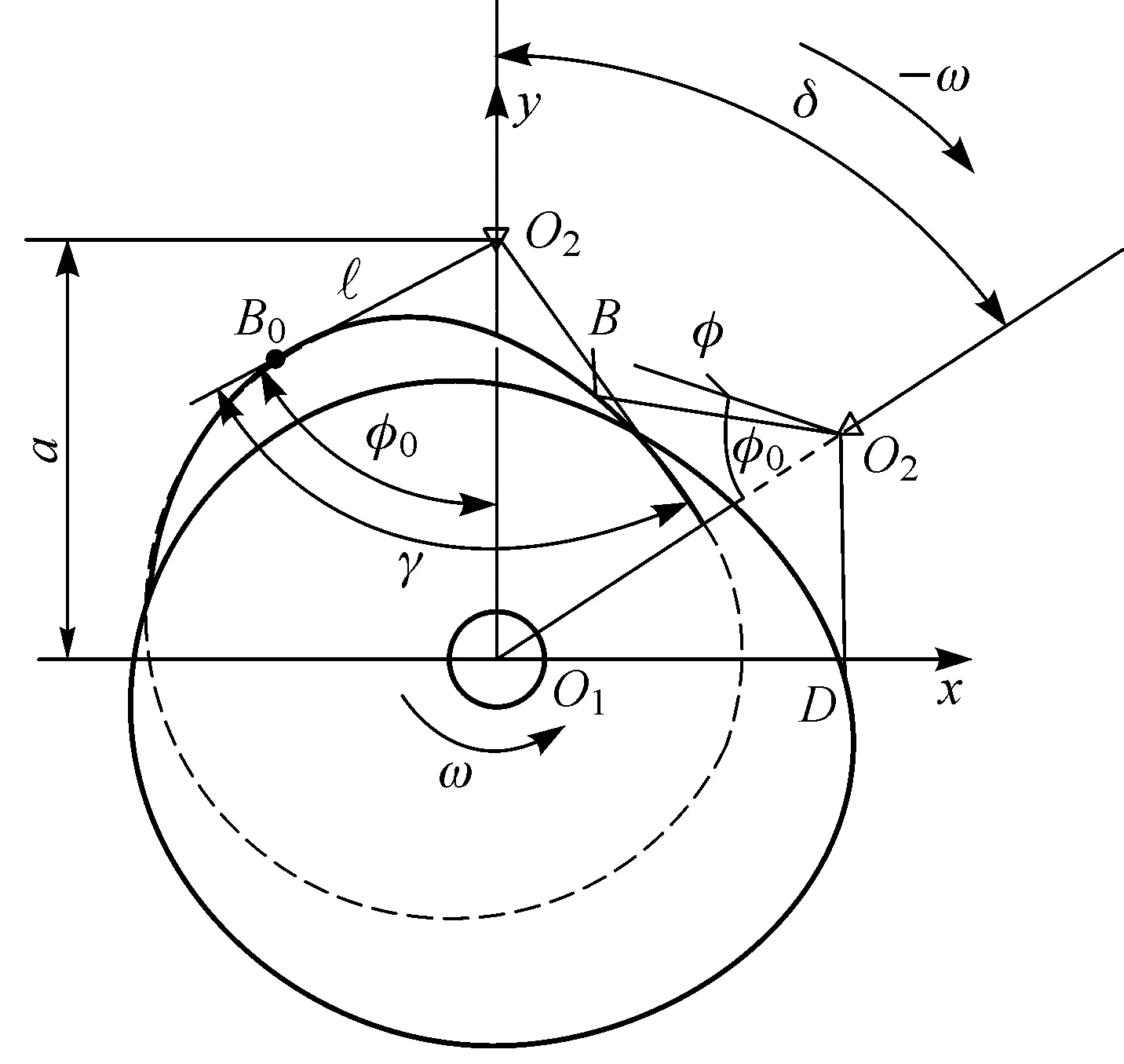
图5 共轭凸轮廓线求解示意图Fig.5 Sketch to solve conjugate cam profiles

本文采用反转法推导凸轮廓线方程.在反转运动过程中，当从动件相对凸轮转过δ角时，从动件处于BO2D位置，此时其角位移为φ，规定构件逆时针转为正，顺时针为负，则B、D点坐标分别为

(8)

(9)

式(8)和(9)即为共轭凸轮理论廓线方程.设滚子半径为R，则共轭凸轮工作廓线方程为

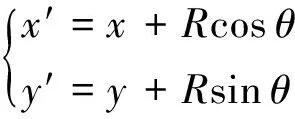
(10)

式中：

(11)

计算主、副凸轮工作廓线时，求得凸轮理论廓线坐标x、y及对应的dx/dδ、dy/dδ，联立式(10)和(11)，即可求得共轭凸轮工作廓线方程式x′、y′.

2.3 基于Matlab的共轭凸轮设计

图6为该共轭凸轮设计软件的流程图.根据该程序流程图可将软件功能划分为3个模块，即，从动件运动规律输入及计算模块，基于许用压力角的凸轮转动中心可行域求解模块，共轭凸轮廓线生成模块.

(1) 从动件运动规律输入及计算模块：输入从动件运动规律以及凸轮转速，计算各时刻从动件的角位移、角速度、角加速度和角跃度.

图6 程序流程图Fig.6 The program flow chart

(2) 基于许用压力角的凸轮转动中心可行域求解模块：输入主、副从动杆夹角γ、许用压力角α、从动杆长以及滚子半径R，求解凸轮转动中心可行域.

(3) 共轭凸轮廓线生成模块：人机交互选定凸轮转动中心，求得共轭凸轮理论及工作廓线，并保存凸轮廓线上的特征点数据.

3 实例验证与仿真

3.1 实例验证

下面是利用本文开发的软件实现某一共轭凸轮机构的设计实例.首先，通过参数输入界面输入从动件分段运动规律及凸轮转速，如图7所示.

点击【预览运动曲线】按钮查看从动件运动规律(如图8所示)，检查运动规律是否有误，必要时进行修改.

运动规律输入完成后点击【参数输入完成】按钮，随之进入凸轮转动中心可行域求解界面，输入相应结构参数后点击【绘制可行域】按钮，程序将求解和绘制满足许用压力角要求的凸轮转动中心可行域(如图9所示).此时，点击【光标拾取】按钮在可行域内选择凸轮转动中心，本例选取点为图9中点O1.

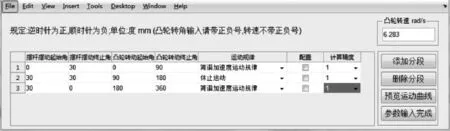
图7 参数输入界面Fig.7 The interface of the parameters input

图8 从动件运动规律预览界面Fig.8 Preview of follower’s motion

图9 可行域求解界面Fig.9 The feasible region of the cam’s rotation center

选取凸轮转动中心后，后台程序计算获得“结构参数变化列表”并予以显示.主、副凸轮最大压力角分别为33.795°和28.417°，均满足许用压力角α=40°的设计要求.点击【查看压力角变化曲线】可以查看凸轮运动过程中压力角变化曲线，如图10所示.确认各设计参数无误后，点击【绘制凸轮廓线】即可获得共轭凸轮工作廓线，如图11所示.

图10 压力角变化曲线Fig.10 The variation curves of the pressure angle

图11 共轭凸轮廓线Fig.11 Profile curves of conjugate cam

至此，已完成满足许用压力角要求的共轭凸轮设计.

3.2 运动仿真

将实例中自动生成的共轭凸轮工作廓线特征数据点导入SolidWorks 2014软件中，生成三维虚拟样机(如图12所示)，并进行运动仿真，其结果如图13所示.

图13(c)中从动杆角加速度的仿真结果存在失真现象，其原因是由于在SolidWorks软件中从动杆与凸轮采用碰撞关系进行运动仿真，仿真软件自身也存在误差.

将以上仿真结果与图8对比可知，本软件所设计的共轭凸轮能较好地满足运动规律设计要求.

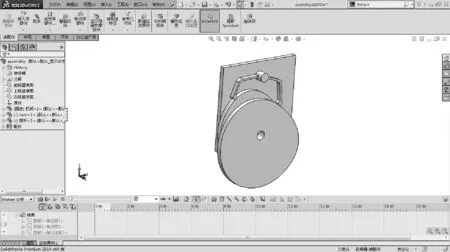
图12 三维模型Fig.12 Three-dimensional model

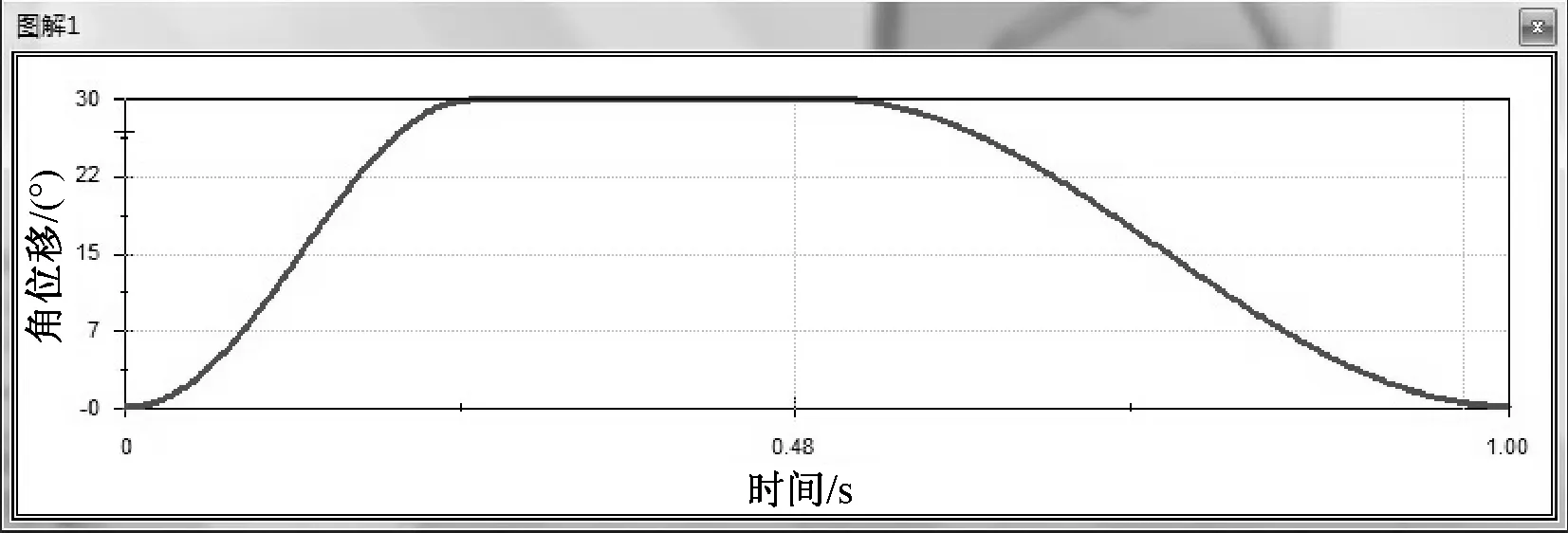
(a) 从动杆角位移

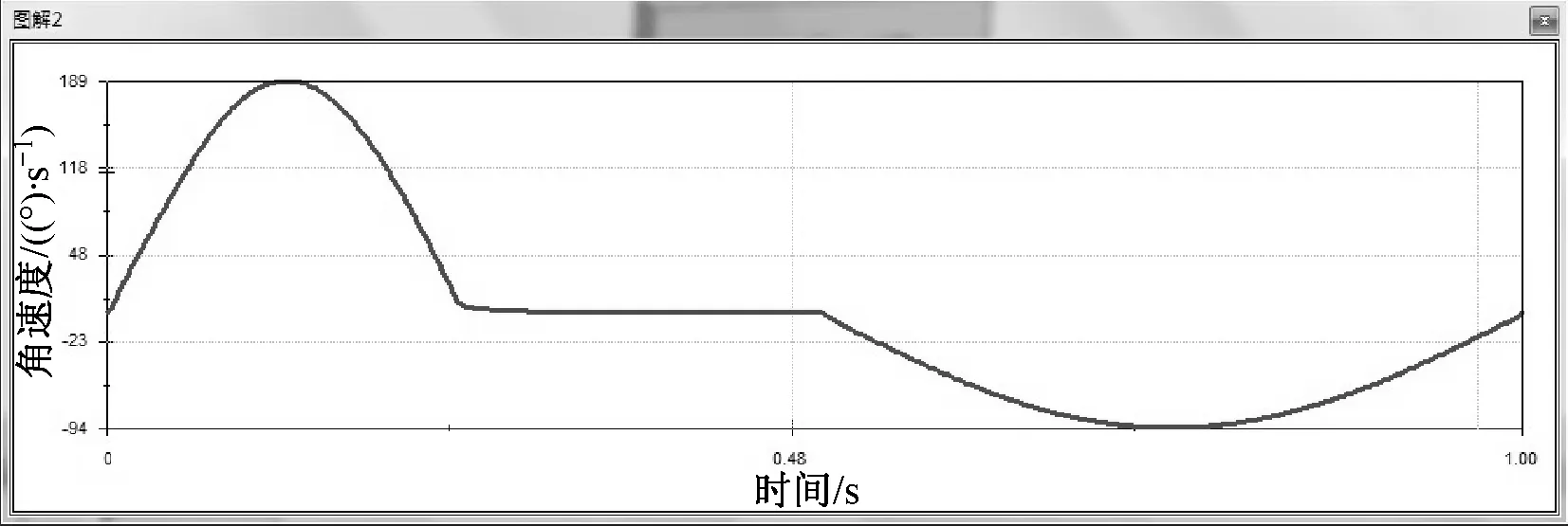
(b) 从动杆角速度

(c) 从动杆角加速度

4 结 语

利用Matlab开发共轭凸轮计算机辅助设计软件，可充分利用Matlab强大的数据处理、图形处理和人机交互能力，借用其GUI对软件进行模块化设计，使编程过程大为简化，同时，友好的人机交互界面便于参数输入、数据查看及结果输出.

压力角是机构传力性能的重要衡量指标，本文研究了基于许用压力角要求的共轭凸轮计算机辅助设计方法，解决了凸轮机构中结构参数设计复杂、使用困难问题.Matlab软件减少了传统设计软件在设计出共轭凸轮廓线后需进行压力角验证的步骤，避免了因压力角大于许用压力角而重复调整结构参数过程，从而大大提高了设计效率.同时，该软件生成的数据文件可直接用于数控加工，实际应用价值高.

[1] 石永刚，徐振华．凸轮机构设计[M]．上海：上海科学出版社，1995．

[2] 方洁.基于LabVIEW的平面盘形凸轮CAD-CAM系统开发[D]．上海：东华大学机械工程学院，2008．

[3] 葛正浩，杨芙莲，彭国勋，等．凸轮机构运动学研究综述[J]．机械设计，2001(3)：45-47．

[4] 陈人哲，陈明．纺织机械设计原理[M]．北京：中国纺织出版社，1996．

[5] 何敏英．织机共轭凸轮的结构参数研究(一)[J]．华东纺织工学院学报，1981，(2)：21-29．

[6] 谢征恒，毛立民，过玉清．基于LabVIEW和Matlab的共轭凸轮打纬机构分析与设计[J]．东华大学学报:自然科学版，2007，33(1)：66-69．

[7] 刘飞，张大伟．基于Pro/E和Adams的共轭凸轮设计与仿真 [J]．机械研究与应用，2011(1)：60-62．

[8] MARIO L, ZABKA P. Design and analysis of conjugate cam mechanisms for a special weaving machine application[J]．Romanian Review Precision Mechanics, Optics and Mechatronics, 2010, 37: 31-38．

The Matlab-Based Development of Conjugate Cam Design

WEIBen1a,1b，SUNZhi-hong1a,1b，LIZi-jun2

( a. College of Mechanical Engineering；b. Engineering Research Center of Advanced Textile Machinery, Ministry of Education, 1. Donghua University， Shanghai 201620, China；2. Shandong Rifa Textile Machinery Limited Company， Liaocheng 252000， China)

To meet the requirement of allowed pressure angle, a conjugate cam computer-aided design software is developed based on Matlab which calculates the feasible region for the location of cam shaft visually. The software can generate the main and vice cam’s profile curves and its characteristic point data automatically after user picks the location of cam shaft from the feasible region through human-computer interaction, which helps to improve the efficiency substantially of conjugate cam’s design. Data files generated from Matlab software can be directly used in computer numerical control machining, so it also has an important practical applications value.

conjugate cam; pressure angle; the feasible region of the location of cam shaft; Matlab

1671-0444(2015)05-0663-07

2015 -03-17

魏 奔(1991—)，男，江西南昌人，硕士研究生，研究方向为机械设计及理论. E-mail: dhubenw@163.com 孙志宏(联系人)，女，教授，E-mail: zhsun@dhu.edu.cn

TH 112.2；TP 391.7

A