微细加工机床立柱结构优化设计

何 剑， 李蓓智， 杨建国， 李 炜

(东华大学 机械工程学院， 上海 201620)

微细加工机床立柱结构优化设计

何 剑， 李蓓智， 杨建国， 李 炜

(东华大学 机械工程学院， 上海 201620)

针对微细加工机床中立柱结构的特殊设计要求，提出一种对立柱结构进行拓扑优化和有限元仿真分析结合的新设计思路.在确定立柱的结构形式后，利用拓扑优化及有限元软件分析立柱受力变化的敏感方向，优化设计结构，并对立柱结构的厚度进行分组建模并进行有限元分析，建立立柱厚度变化与受定载荷变形量之间关系曲线，选择最佳厚度，最终确定立柱结构的最佳结构模型.优化设计后的立柱结构质量减轻，刚性增加，证明该优化设计过程有效可行.

微细加工机床； 立柱设计； 结构优化设计； 拓扑优化； 有限元分析

随着科技的发展，微型化、小型化制造逐渐占据着加工层面的部分重要领域，尤其是航空、航天、医疗等领域，对于纳米级精度的零部件的需求更为迫切，这使得微细加工设备的研究也随之迅速发展.立柱支撑件作为机床的关键基础部件之一，国内外学者根据不同加工机床的需求，对其进行过各种结构优化设计及分析[1-2]. 根据设计变量的不同，结构优化可以分为尺寸优化、形状优化、拓扑布局优化和结构类型优化[3].本文所优化的立柱结构是用于微细加工机床上，支撑z轴方向(重力方向)运动工作台及电主轴等部件，微细加工机床的加工精度需达到1 μm以下，因此，对机床立柱的变形量控制要求很高.为此，本文将结合有限元分析软件对机床立柱结构进行优化设计及分析.

1 微细加工立柱对比分析

目前常见的立柱结构形式有两种，即龙门式立柱和C型立柱，两种立柱各有其优缺点.采用同样的运动结构安装在两种立柱结构上的情况如图1所示.

(a) 龙门式立柱

(b) C型立柱

当微细加工机床的垂直运动精密进给工作台与立柱结构的安装接触面积较大，采用如图1(b)所示的立柱结构时，将会出现立柱的负载重心到平台表面距离急剧增大的问题，直接导致立柱与垂直精密进给工作台行程的悬臂梁结构的悬臂过长. 从图1可以看出，C型立柱的运动机构重心距离立柱与平台安装面距离比龙门式结构的要低很多，即稳定性比龙门结构强.从立柱与平台安装接触面积角度考虑，C型立柱结构相对龙门立柱有更大的安装接触面积，可以设计法兰面，即可以保证3条接触边，而龙门立柱结构有2个支撑脚的截面面积去支撑整个立柱及其负载重量，静力学特性没有C型立柱结构优.图1(b)的结构既保证了C型立柱的高稳定性及大接触面的优点，又具有龙门结构的大运动空间的优点.因此，本文对C型立柱结构经过优化设计可满足质量最小且刚性最强的要求.

2 立柱结构优化设计

2.1 优化设计思路

某微型加工机床结构如图2所示，立柱由两侧的伸出边与下方的工作台进行固定连接.立柱负载主轴、夹具及z轴方向运动工作台的重量，工作情况下还需额外负载加工中产生的切削力.由于加工精度要求高，这对立柱的整体结构刚性提出了很高的要求.结合重心高则稳定性差这个理论，要求整机的重心高度尽量降低，即在不影响加工精度以及立柱系统刚性的前提下，需要整机上方包括立柱在内的质量尽量小.因此，从整机的加工稳定性以及加工精度角度而言，立柱结构优化设计的重点在于增强刚性和减少质量.

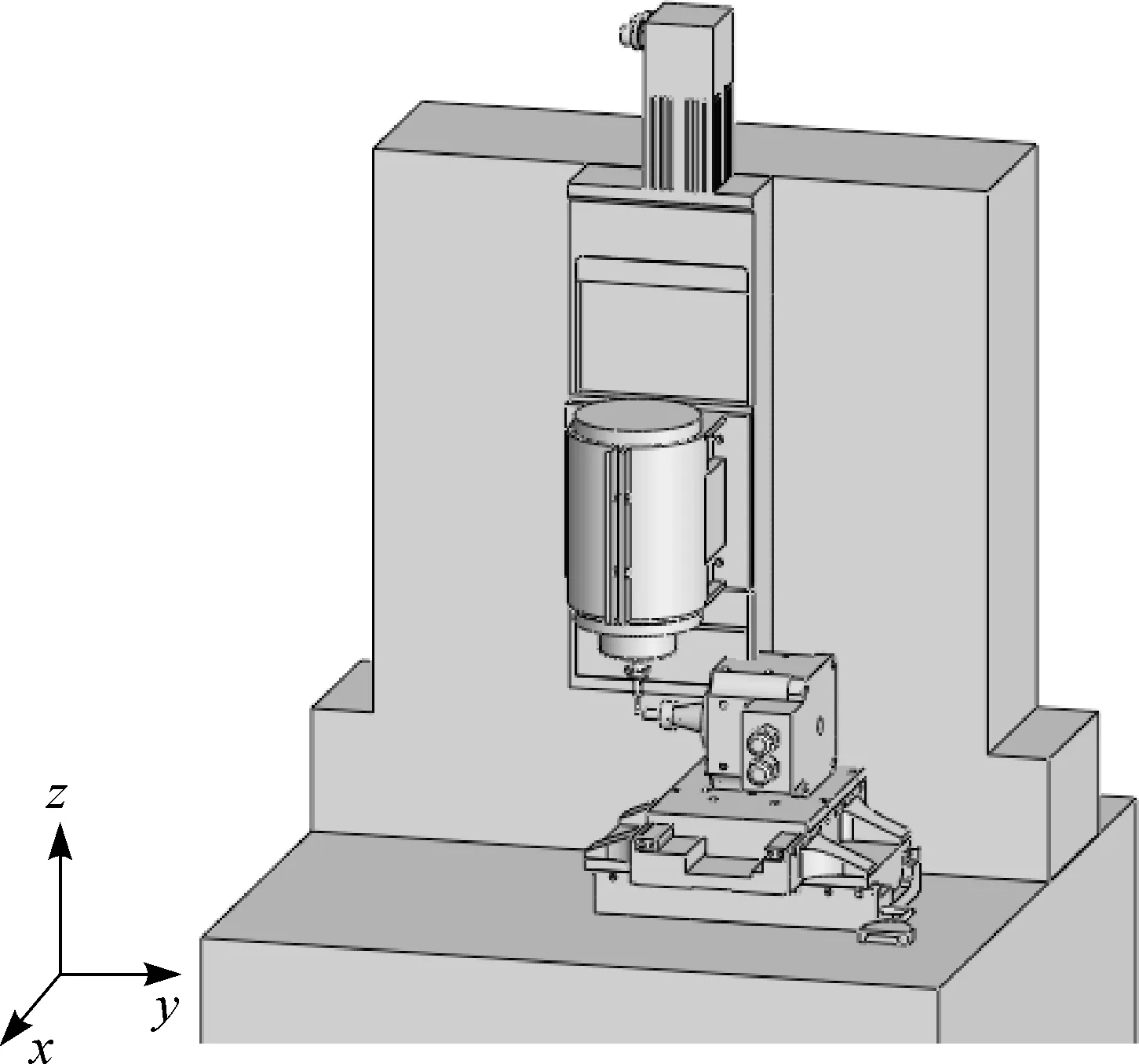
图2 微细加工机床的三维结构简图Fig.2 The 3D structure diagram of micro-machine tool

通过拓扑优化分析技术，初步确定出立柱的基本外形结构，并对优化前后的立柱结构进行有限元分析对比，分析最大位移变形量，最终确定拓扑优化后的外形尺寸结构.在此基础上，分析立柱厚度对其整体刚性的影响，找出厚度与刚度间的变化关系，选择最佳厚度，计算并验证分析结果[4].基于这一设计思路的立柱结构优化设计的流程如图3所示.

图3 立柱结构的优化设计基本思路Fig.3 The basic idea of the optimized design for pillar structure

2.2 优化设计方法

2.2.1 有限元建模

在Solidworks软件中，对立柱结构进行三维建模，建模过程中对其中无关紧要的微小特征结构予以简化，减少不必要的工作量.然后将建立的三维模型导入到ANSYS Workbench软件中.

在ANSYS Workbench的分析环境下，设置立柱的材料属性，立柱为大理石材，故设定弹性模量为70 GPa，抗拉强度为200 MPa，密度为2.8×103kg/m3以及泊松比为0.3.利用Sizing功能对三维结构进行网格设置和划分，如图4所示，然后对模型设置边界条件和优化目标.为了简化计算，在模型的载荷设计中，将主轴系统部分重量对立柱产生的弯矩作用，简化为一个施加在z轴方向运动工作台与立柱的接触面积上的力矩.

图4 立柱三维模型的网格划分Fig.4 Meshing of 3D model of the pillar

2.2.2 拓扑优化方案

将拓扑优化后结果反馈给设计人员，并做出适当的修改，一般为更为细致的形状、尺寸以及自由形状的优化. 拓扑优化后结果为概念设计方案，经过设计人员修改过的设计方案为最优设计方案. 最优设计方案往往比概念设计方案的结构更轻、性能更佳. 拓扑优化的特点是在给定的设计空间中找到最优的材料分布.

拓扑优化的数学模型可表述为

约束条件:

gj(X)≤0j=1, 2, …，m

hk(X)=0k=1, 2, …,mh

式中：f(X)为目标函数；X=x1,x2, …,xn为设计变量；g(X)为不等式约束函数；h(X)为等式约束函数；上角标L代表下限；上角标U代表上限.

在OptiStruct中，目标函数f(X)、约束函数g(X)与h(X)是从有限元分析中获得的结构响应.在拓扑优化中，设计变量X为单元的密度[3]. 拓扑优化的目标是要求结构柔度能量极小化，即要求结构刚度的最大化.为了解拓扑优化的结构变化趋势，设置一系列的梯度目标值，采用质量缩减的方法，设置了3个目标缩减值，并依次对立柱结构进行拓扑优化计算.计算结果如图5所示.

(a) 15%

(b) 10%

(c) 5%

由分析图5中的优化结果可知，受到外加载荷的情况下，结合实际加工中的可操作性，可选取的去除部分是立柱两侧的部分，形成一个梯形的截面，其优化后的体积较原结构减少10.8%，优化后的立柱型式如图6所示.

图6 优化后立柱模型Fig.6 The optimization model of the pillar

3 立柱结构优化方案效果验证

立柱结构的变形主要受到自身重量以及前表面负载部件的重量影响，而前端负载的重量对于立柱形成了一个力矩作用.因此，在做静力学仿真分析时，需要考虑这一问题并加以处理.在有限元分析软件Abaqus中，将前端负载重量进行质量集中，找出其质心坐标，并且将该质点与立柱接触面建立耦合关系.在该质点上施加作用力代替重量作用，如图7所示，其中O即为质心参考点.

图7 静力学分析中质心点设置及网格划分Fig.7 Centroid point setting and meshing of statics analysis

假定立柱厚度为350 mm，在相同的情况下，设计对应的龙门式立柱，根据机床的安装高度设计立柱的架空高度为200 mm，并且需要与C型立柱保持相同的安装面积，则建立如图8所示的三维模型.

图8 龙门式立柱三维模型Fig.8 3D model of gantry column

将优化前后的C型立柱模型以及龙门式立柱模型导入软件，施加等同于运动机构重量的外力作用后，其变形情况如表1所示.

表1 立柱优化前后的变形情况对比

优化后的两个三维模型，在三维软件中可通过体积分析来对比其质量变化.因此，对比表1中优化前后的结果可知，质量减少9.8%，同一参考点最大位移量减少8.9%，满足质量减小刚度增加的要求，相对优化前参考点最大位移变形量减小33.7 nm.龙门式立柱的变形量要比优化后的C型立柱多44.5%.基于此考虑，优化后的C型立柱结构具有更好的刚性和更轻的质量，可作为本机床立柱设计中的最佳方案.

4 结 语

基于初始的边界限定条件，首先定性地对传统的2种立柱结构进行分析对比，然后针对可优化的C型立柱进行结构优化，利用拓扑优化的方法确定立柱结构的基础结构形状.在分析影响立柱刚度的厚度因素时，利用有限元仿真软件进行静力学受力分析，建立厚度与刚度的变化关系曲线，找到合适的拐点，对应最佳立柱厚度.最后将优化前后的立柱结构及对应相同边界条件下的龙门结构进行有限元分析对比，得出优化后的立柱结构比优化前最大变形量减少了8.9%，质量减少了9.8%，比龙门式立柱最大变形量减少了44.5%.证明优化后的立柱结构是适合于当前机床的最佳结构形式.

[1] 王泉森.龙门铣床结构分析及优化设计研究[D].长春：长春工业大学机电工程学院,2012:9-10.

[2] 马超.机床结构设计方法研究及在立柱设计中的应用[D].大连：大连理工大学机械工程学院,2010:10-18.

[3] 李范春.ANSYS Workbench设计建模与虚拟仿真[M].北京：电子工业出版社,2011:256-257.

[4] 朱金波,王宇,阳红，等.基于转移质量方式的龙门加工中心动横梁结构优化设计方法[J].机械设计与制造,2012(9)：19-30.

Structural Optimization Design for Pillar of Micro-machine Tool

HEJian,LIBei-zhi,YANGJian-guo,LIWei

(College of Mechanical Engineering, Donghua University, Shanghai 201620， China)

According to the special requirements of pillar in micro-machine tool structural design, a new structural optimization design method is introduced which is combined topological optimization method and FEM (finite element method) simulation analysis theory. After making sure of the basic structure of the frame, it takes use of topological optimization and FEM simulation analysis theory to do the stress analysis at the sensitive direction of the frame, and then proceeds the structural optimization. Meanwhile, different models are built according to the thickness of pillar for FEM simulation analysis, and then the relationship curve of frame thickness value and mechanical deformation value is established, finally, optimum thickness of pillar and the corresponding frame structure model are obtained. The lighter quality and better stiffness of pillar after optimization design prove that this method works efficiently.

micro-machine tool； pillar design； structural optimization design； topology optimization； finite element analysis

1671-0444(2015)05-0659-04

2014-03-03

国家八六三高技术研究发展计划资助项目(2012AA041309)

何 剑(1988—)，男，湖北黄冈人，硕士研究生，研究方向为微细加工机床设计. E-mail:owendw@163.com 李蓓智(联系人)，女，教授，E-mail: lbzhi@dhu.edu.cn

TH 122

A