基于异常点剔除的高压直流输电线路故障定位算法

丘映丹，李海锋，郭履星，梁远升，王小立，罗美玲

(1．华南理工大学电力学院，广州市510640;2．国网宁夏电力公司，银川市750001)

0 引言

直流输电技术是解决我国能源和负荷中心分布不均带来的电能远距离大容量传输问题的重要技术手段之一［1-2］。在实现能源和电力资源的优化配置、解决区域交流电网互联的稳定运行以及大规模新能源电力的接入问题上，直流输电技术发挥了重要的作用。目前，我国建成的高压直流输电线路已经超过20条，其中包括云南—广东±800 kV等3条特高压直流输电工程，使得我国已经成为世界上直流输电电压等级和输送容量最高的国家［3-4］。可见，保证直流

输电系统的安全稳定运行具有极其重大的意义。

直流输电线路距离长，发生故障的概率大。据统计，直流系统故障中输电线路故障占50%，因此实现直流输电线路快速准确的故障定位是保障大电网安全、稳定和经济运行的重要技术手段［5-6］。行波法依据行波传输理论进行故障定位，其实现定位原理简单，在实际直流工程中被广泛采用［7］。行波法在理论上不受故障类型和过渡电阻的影响，但是在实际工程中受到很多因素的制约，例如行波的获取、波头的准确识别以及波速确定等［8-9］。此外，行波法要求的采样频率很高，其硬件投资成本较大。

近年来，根据系统的线路参数以及电压电流量，通过分析计算得到故障点位置的时域故障分析法受到了广泛的关注。与行波法局限于波头数据不同，故障分析方法不依赖于行波波头的准确标定，在理论上能利用故障后从暂态到稳态的所有暂态数据进行故障定位，无须时域－频域转换，对装置采样率要求低，具有一定的实用价值，能够作为行波法的有效补充［10-12］。

然而该方法的准确性依赖于精确的线路模型。现有时域故障分析方法都是基于恒定参数的贝瑞隆(bergeron)线路模型，这与实际输电线路的参数频变特性(frequency-dependent)具有一定的差异。由于直流输电系统传输直流电气量，而在故障时则具有大量的高频信号，频带范围很广，使直流线路参数频变特性对基于恒定参数模型的故障定位方法的影响较交流系统更加突出。由于该影响程度与直流线路故障暂态过程中的行波传播特性及其频率成分有关，造成故障定位的误差随故障暂态过程不同发展阶段而有所不同，具有一定的随机性。因此，充分利用故障后从暂态到稳态的电气信息量进行故障定位，是提高时域法故障定位结果准确性和稳定性的有效途径。

为此，本文提出一种基于异常点剔除的直流输电线路故障定位算法。该算法在现有基于分布参数的时域故障定位算法的基础上，充分利用故障后的暂态数据，采用冗余数据窗移动，将测量得到多个定位结果作为数据集，采用统计学中基于距离的异常数据处理方法将数据集中的异常数据剔除，从而得到最终的定位结果。最后，基于PSCAD/EMTDC软件搭建云南—广东±800 kV双极直流系统模型对所提算法进行验证分析。

1 双极直流输电线路的相模变换

图1给出了双极直流输电系统的简化模型。

对于图1的双极直流输电线路，假定线路为均匀传输线，可以得到输电线路的均匀传输线方程为

图1 双极直流输电系统模型Fig.1 Bipolar DC transmission system model

式中:［uphase］=［uPuN］T、［iphase］= ［iPiN］T分别为极线电压、电流列向量;［R］、［L］、［G］、［C］分别为直流输电线路单位长度的电阻、电感、电导以及电容。

对于双极直流输电线路可以构造解耦矩阵为

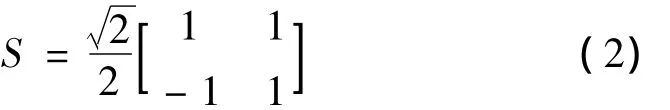
由式(2)的相模变换矩阵，式(1)可以写成以下模量的形式:

式中［um］=［u1u0］T、［im］=［i1i0］T，可以将 u1、i1称为线模电压、电流分量，u0、i0称为地模电压、电流分量。

由于地模分量是以大地形成回路，其稳定性受影响较大，本文采用较为稳定的线模分量进行计算。

2 沿线电压分布计算

在贝瑞隆参数模型下，由输电线路两端的电气量可以得到沿线电压分布计算公式为

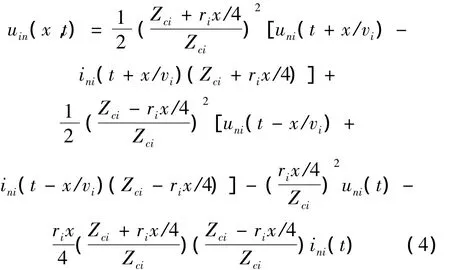
式中:uin(x，t)是利用n端电气量计算出的、距离x处的i模电压，n为J、K分别表示直流线路的两端，i=，1为模量标号，分别表示地模、线模;riici分别是i模的电阻率、波速和特征阻抗;uni(t)、ini(t)分别是在t时刻n端的i模电压、电流。

3 故障定位判据构造

3.1 固定数据窗的定位判据构造

故障发生时，由于受到对端注入电流的影响，从两端计算得到的沿线电压分布应在故障点处具有差值最小的特点。现有基于分布参数模型的时域故障定位算法，增加一段冗余数据窗，构造如下的故障定位函数［10］:

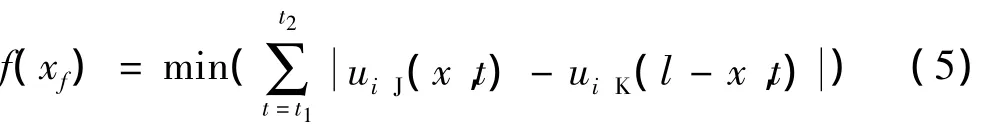
式中:l为输电线路的全长;x为距离整流侧J端的距离;△t=t2－t1为所取的冗余数据窗的长度。

在理论上，故障定位函数取最小值得到的结果即为故障位置。但在实际工程中，由于直流系统较为明显的频变特性，所取冗余数据窗对定位结果会产生直接的影响。当在某一时刻计算得到的沿线电压分布在故障点处的差值比非故障点处的差值要大很多的时候，在一段时间内的积分就未必能保证在故障点处具有差值最小，从而得到的定位结果可能就不是真实的故障位置。因此，现有时域法采用固定的时间窗进行计算得到结果的可靠性得不到保障，而且并没有完全利用故障后的所有暂态信息量。

图2给出了基于云南—广东±800 kV双极直流输电模型(线路全长1 374 km)，分别在距离整流侧300 km处发生金属性接地、500 km处经过500 Ω过渡电阻接地以及线路中点(687 km)发生金属性接地时，采用6 ms的数据，平移数据窗得到的故障定位结果的误差。其中横坐标表示每隔0.2 ms平移数据窗得到定位结果的顺序，纵坐标表示平移数据窗得到的故障定位结果的误差。

图2 随数据窗平移故障定位结果Fig.2 Fault location results when translating data window

可见随着数据窗的推移，得到的定位结果并不是完全一致的，而是存在一定的波动。更重要的是，在不同的故障位置以及不同的故障条件下，在同一数据窗得到的定位结果的精度并不是一致的，而是存在较大的差异。因此，在故障定位中，有必要考虑数据窗不同对故障定位结果的影响。

3.2 基于异常点剔除的定位判据构造

为了保证得到定位结果的可靠性，充分利用故障后的暂态信息，本文提出一种基于异常点剔除的故障定位算法。通过不断平移冗余数据窗得到多个定位结果，考虑到在多个冗余数据窗内得到的结果只有小部分是故障定位函数的伪根，采用基于距离的异常数据处理的方法得到邻域集合中数目最多的集合，进而求取该集合中数据的平均值作为故障定位结果。

如图3，假定装置的采样频率为f，取故障后的一段数据窗T，每隔t时间取一段冗余数据窗△t，依据提出的故障定位算法，在T时间内可以得到(T/t+1)个故障定位结果。

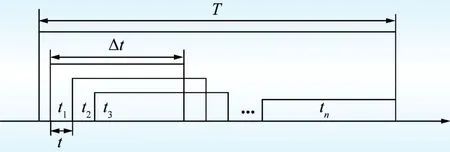
图3 平移数据窗示意简图Fig.3 Schematic diagram of translating data window

如图3所示，每隔t时间平移数据窗，在ti(i=1，2，…，n)冗余数据时间窗内采用式(5)中的故障定位函数，可以得到定位结果xfi(i=1，2，…，n)。

为了保证定位结果的精度，需要进一步对得到的结果进行处理。在此不妨假设平移数据窗得到的结果为一数据集。由于参数的波动以及输电线路的依频特性对故障定位结果的影响是模糊和随机的，所以在不同的故障条件下，采用不同的数据窗进行计算得到的结果的精度具有随机性。因此，并没有办法事先知道数据集的分布。

在统计学中，对异常数据还没有一个普遍可以接受的定义。在不同的领域以及采用不同的检测方法，异常数据的定义也不同［13］。从本文的研究目的出发，考虑样本数据集分布的未知性，本文借鉴统计学中一种基于距离(distance-based)的异常数据处理方法。

基于距离的异常点的定义为:设存在一m维点的集合A:

式中:Oi为A中的数据;xip为Oi的p个分量。

定义A中的任意2点Op、Oq间的绝对距离为

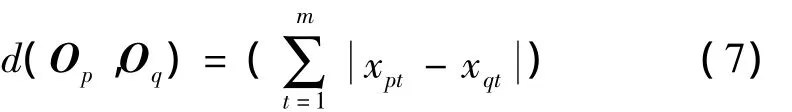
对于A中的任一点Op，给定一个正数D＞0，若点集合中的任一点Oq满足条件:d(Op，Oq)＜D，则称Op为Oq的D-邻近点，称所有 D-邻近点的集合为Op的 D-邻域。

根据以上分析，将得到的定位结果xfi组成的集合作为样本数据集A，设定D的值，得到临界邻居数目最多的点的集合，即求出D-邻域所含数据最多的集合，可将该集合视为已剔除异常数据的集合。进一步对该集合中的数值求取平均值，并将此平均值作为故障定位的结果。

根据以上分析，图4给出了本文提出故障定位算法的基本流程图。

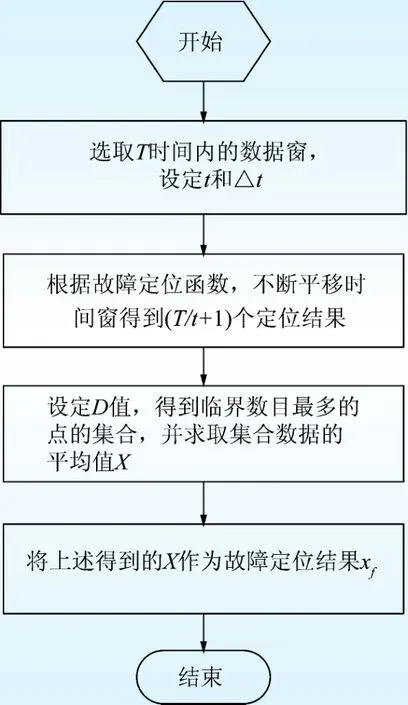
图4 基于异常点剔除的故障定位算法流程图Fig.4 Flow chart of fault location algorithm based on picking out outliers

4 仿真分析

利用PSCAD/EMTDC电磁暂态软件，基于实际工程参数搭建了云南—广东±800 kV双极直流输电系统仿真模型，其结构简图如图1所示。其中，线路全长为1 374 km，线路模型采用频变参数模型。在仿真计算中，取故障后一段数据窗T为6 ms，总数据长度约为16 ms，数据采样频率f为100 kHz，每隔0.2 ms取一段冗余数据窗△t为3 ms，设定D为5 km。

为了验证本文提出算法的有效性，在不同故障情况下进行了大量的仿真分析。表1给出了本文提出的故障定位算法，在不同的故障位置和不同的过渡电阻下得到的定位结果。

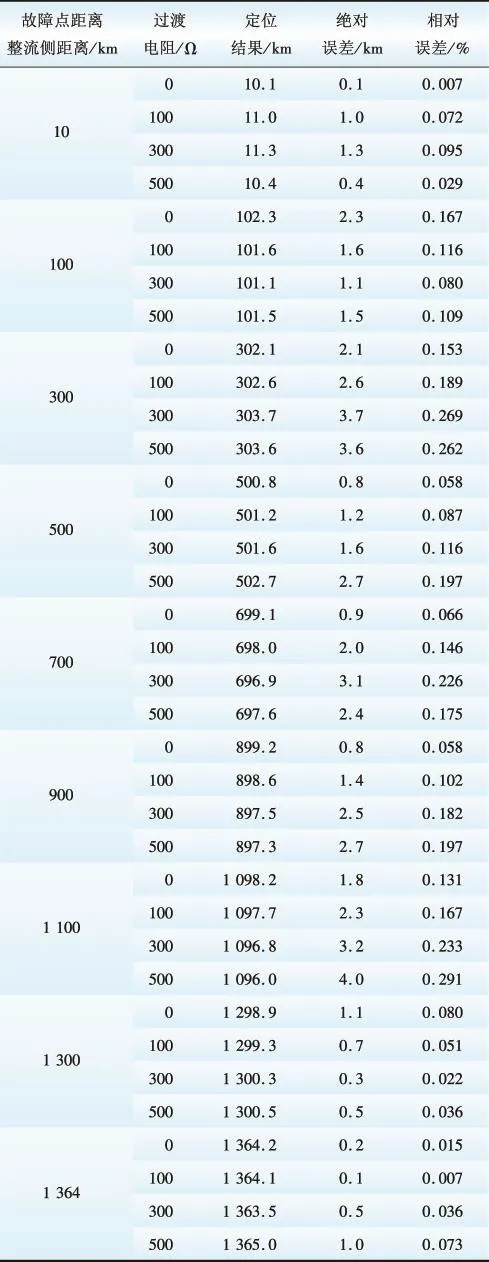
表1 基于异常点剔除的故障定位结果Table 1 Fault location results based on picking out outliers

由表1的故障定位结果可见，本文所提出的基于异常点剔除的时域故障定位算法在大过渡电阻的条件下仍能实现线路全长范围内的准确定位，最大定位误差不超过线路全长的0.3%。

现有时域故障定位算法中采用3 ms的冗余数据窗进行仿真分析，定位结果最大误差为12 km，相对误差为线路全长的1.2%［10］。图5给出了基于云南—广东±800 kV直流输电系统，冗余数据窗取3 ms，在不同位置、经不同过渡电阻接地时得到的定位结果的绝对误差的变化折线图。其中横坐标为故障位置距离整流侧的距离，纵坐标为定位结果的绝对误差。

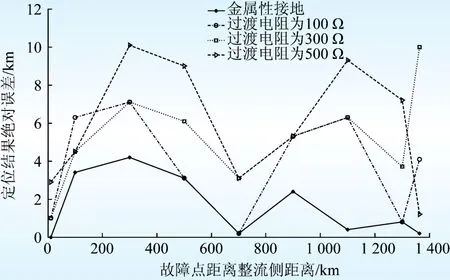
图5 定位结果绝对误差变化折线图(冗余数据窗取3 ms)Fig.5 Line graph of absolute error change of fault location results with 3 ms redundancy

从图5可知，采用现有的时域故障定位算法，采用3 ms的冗余数据窗进行故障定位时，定位结果最大绝对误差约为10 km，相对误差约为线路全长的0.73%。

为进一步说明本文提出算法的有效性，图6给出了在与图5相同条件下，冗余数据窗取6 ms的定位结果绝对误差变化折线图。

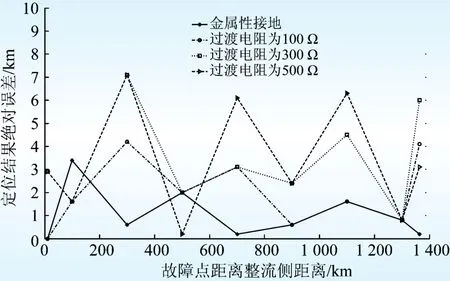
图6 定位结果绝对误差变化折线图(冗余数据窗取6 ms)Fig.6 Line graph of absolute error change of fault location results with 6 ms redundancy

对比图5和图6，在相同条件下当冗余数据窗增加至6 ms时，最大定位误差减小至7 km，但其定位精度仍低于本文所提算法的定位精度。可见，适当增加数据窗的长度能在一定程度上减小故障定位的误差，但是通过对故障定位结果的异常数据的处理，能进一步提高故障定位结果的精度和可靠性。

本文算法是以两端数据同步为基础的，这也是算法在实际工程应用中必须解决的问题。为了分析本文算法受双端数据同步时间存在偏差的影响，结合算法所需的采样频率(100 kHz)，分析双端数据同步时间存在10 μs误差时的故障定位情况，结果如表2所示，其中，除数据非同步外其他仿真条件设定同表1。

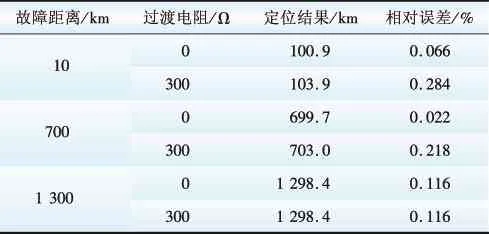
表2 故障定位结果(双端数据非同步)Table 2 Fault location results with unsynchronized two-end data

从表2可知，当双端数据即使存在一定的非同步偏差时(10 μs)，对本文所提算法的故障定位结果影响不大，最大相对误差仅增加0.015%。由于目前在电力系统的控制保护系统中，双端数据同步均采用全球定位系统(global positioning system，GPS)，而GPS的时间精度要远远高于本文所提算法的要求，如实际行波测距装置的GPS时钟在稳定运行时其精度可达到1 μs，甚至更高。且随着研究的不断深入，高精度时钟的产生得到了更多技术的支持，时钟精度甚至可达ns级别［14-15］。由此可见，按目前工程上实际装置的同步时钟性能，已完全能够满足本文所提方法对于数据同步的要求。

5 结语

本文提出了一种基于异常点剔除的直流输电线路时域故障定位算法。该算法在现有时域故障定位算法的基础上，通过不断平移冗余数据窗得到多个定位结果，采用基于距离的异常数据处理方法，对得到的定位结果进行异常数据处理，进而得到最终的定位结果。仿真结果表明本文提出的算法不局限于波头数据，即使在大过渡电阻下仍能实现线路全长的准确故障定位;该算法提高了故障定位结果的精度和可靠性。

95

［1］李立浧．直流输电技术的发展及其在我国电网中的作用［J］．电力设备，2004，11(5):1-5．Li Licheng．Development of HVDC transmission technology and its role in power network in China［J］．Electric Equipment，2004，11(5):1-5．

［2］梁旭明，张平，常勇．高压直流输电技术现状及发展前景［J］．电网技术，2012，36(4):1-9．Liang Xuming，Zhang Ping，Chang Yong．Recent advances in highvoltage direct-current power transmission and its developing potential［J］．Power System Technology，2012，36(4):1-9．

［3］姚良忠，吴婧，王志冰，等．未来高压直流电网发展形态分析［J］．中国电机工程学报，2014，34(34):6007-6020．Yao Liangzhong，Wu Jing，Wang Zhibing，et al．Pattern analysis of future HVDC grid development［J］．Proceedings of the CSEE，2014，34(34):6007-6020．

［4］Bahrman M P，HVDC transmission overview ［C］//2008 IEEE/PES Transmission and Distribution Conference ＆ Exposition．Chicago:IEEE，2008:1-7．

［5］胡婷，游大海，金明亮．输电线路故障测距研究现状及其发展［J］．电网技术，2006，30(增刊):146-150．Hu Ting， You Dahai， Jin Mingliang． Presentsituation and development of fault location for transmission lines［J］，Power System Technology，2006，30(Supplement):146-150．

［6］宋国兵，蔡新雷，高淑萍，等．高压直流输电线路故障定位研究综述［J］．电力系统保护与控制，2012，40(5):133-147．Song Guobing，Cai Xinlei，Gao Shuping，et al．Survey of fault location research for HVDC transmission lines［J］．Power System Protection and Control，2012，40(5):133-147．

［7］ Farshad M，Sadeh J．A novel fault-location method for HVDC transmission lines based on similarity measure of voltage signals［J］．IEEE Transactions on Power Delivery，2013，28(4):2483-2490．

［8］马超然．输电线路行波故障定位技术发展与展望［J］．继电器，2007，35(24):11-15．Ma Chaoran．Prospect and development of transmission line fault location using travelling wave［J］．Relay，2007，35(24):11-15．

［9］ Zhang Y N，Liu Y H，Xu M，et al．A novel algorithm for HVDC line fault location based on variant travelling wave speed［C］//2011 4th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies．Weihai:IEEE，2011:1459-1463．

［10］宋国兵，周德生，焦在滨，等．一种直流输电线路故障测距新原理［J］．电力系统自动化，2007，31(24):57-61．Song Guobing，Zhou Desheng，Jiao Zaibin，et al．A novel fault location principle for HVDC transmission line［J］．Automation of Electric Power Systems，2007，31(24):57-61．

［11］Liang Y S，Wang G，Li H F．Time-domain fault-location method on HVDC transmission linesunderunsynchronized two-end measurement and uncertain line parameters［J］．IEEE Transactions on Power Delivery，2015，30(3):1031-1038．

［12］Suonan J L，Gao S P，Song G B．A novel fault-location method for HVDC transmission lines［J］．IEEE Transactions on Power Delivery，2010，25(2):1203-1209．

［13］孟静．异常数据挖掘算法研究与应用［D］．无锡:江南大学，2013．Meng Jing．Outlier mining algorithm research and appliation［D］．Wuxi:Jiangnan University，2013．

［14］蒋陆萍，曾祥君，李泽文，等．基于GPS实现电力系统高精度同步时钟［J］．电网技术，2011，35(2):201-206．Jiang Luping，Zeng Xiangjun，Li Zewen，et al．Realization of high accuracy synchronous clock for power system based on GPS［J］．Power System Technology，2011，35(2):201-206．

［15］童伟．基于北斗II代/GPS的电力系统双模时间同步时钟的研制［J］．电力建设，2014，35(4):81-85．Tong Wei．Development of Beidou II/GPS dual-mode synchronization clock for power system ［J］．Electric Power Construction，2014，35(4):81-85．