考虑线路介数和well-being风险贡献度的电网脆弱线路评估

熊世旺，郭创新，何宇斌，王威，谢宇哲

(1．浙江大学电气工程学院，杭州市310027;2．国网浙江省电力公司宁波供电公司，浙江省宁波市315000)

0 引言

电力系统大停电事故的频繁发生，引起了学者对电网脆弱性的广泛关注［1-2］。近年来，许多研究成果表明，停电事故往往是由于少量薄弱环节［3］发生故障，导致电网传输能力不断弱化，进而引起大停电事故。

目前，电网脆弱性研究主要从网架结构和网络运行状态2方面进行。在网架结构方面，基于复杂网络理论［4-5］，从电网拓扑角度出发，研究网络节点度数和线路介数 以及电网的小世界特性 在电网实时运行状态方面，基于可靠性追踪方法，追踪系统元件对系统可靠性的“贡献”程度，辨识电网的薄弱环节［10-11］，也有学者在此基础上提出了well-being风险追踪模型［12］，通过警戒贡献度和紧急贡献度指标进行元件脆弱性评估和排序。有学者指出，在导致电网脆弱性的诸多因素中，电网的网架结构和运行状态是2个相互紧密联系的重要方面，脆弱性评估需要同时考虑电网的网架结构和实时运行状态。已经有一些文献在综合脆弱性［13-14］方面进行了一些研究，文献［15-16］提出利用线路介数和潮流熵相结合的方式进行脆弱线路评估，但是潮流熵比较抽象，并且这些评估方法无法计及概率因素的影响，也无法反映实时运行环境变化的影响。

为了更好地对输电线路进行脆弱性评估，本文提出一种综合考虑线路介数和well-being风险贡献度的输电线路脆弱性评估方法。在网架结构方面运用加权介数模型，采用线路介数描述线路在电网结构位置上的重要程度。基于well-being风险追踪模型，提出记及元件敏感度的well-being风险贡献度指标。同时，采用两状态天气模型量化恶劣天气对线路故障率的影响程度。结合线路介数和well-being风险贡献度提出综合脆弱性指标，基于该指标和非序贯蒙特卡洛法提出输电线路脆弱性评估方法流程，从电网的运行状态和网架结构2方面评估线路的脆弱性。最后通过对IEEE-RTS系统进行仿真来验证所提方法的合理性和实用性。

1 线路介数

在脆弱性评估中，线路介数一般定义为电网中线路被网络中所有电源节点与负荷节点之间的最短路径经过的次数［17］，即

式中:Bi为线路介数;V为网络节点集;Njk(i)为网络中任意两节点j和k之间的最短路径经过线路i的次数。

式(1)并未考虑线路权值，但线路之间存在着广泛的电气联系，不考虑线路权值无法反映网络线路之间的电气联系。因此有学者提出了加权介数模型，在无权值网络拓扑模型中引入了线路电抗值，将其作为边的权重［18-19］，提出了使用加权线路介数作为脆弱线路指标的辨识方法。与此同时，对节点间最短电气路径也重新进行了定义，将最短路径定义为从电源节点到负荷节点之间经过的线路中电抗和最小的路径。线路介数越大，表明该线路在网络中的位置越关键，同时在电源节点和负荷节点之间起到的电能传输作用越大，该线路被切除或发生故障对电网拓扑结构的影响越显著。

加权介数模型计算出的线路介数，更多地是从网架结构上来表现电网的脆弱性，属于电网的固有属性，是脆弱性评估的一方面。在电网实际运行时，高介数线路出现故障的概率大小，线路开断对整个系统的状态有何影响等问题，并不能用加权介数模型来说明。

2 well-being风险贡献度

2.1 设备故障率模型

输电线路属于暴露在外的设备，恶劣天气对输电线路的运行状态影响非常显著。为了量化天气状况对输电线路故障概率的影响，本文采用两状态天气模型［20］。在正常天气、恶劣天气情况下设备元件的年故障率分别为:

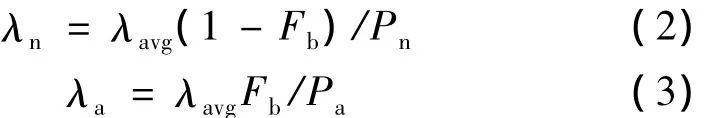
式中:λavg是元件年平均故障率;Fb是故障发生在恶劣天气情况下的比例;Pn、Pa分别为基于历史统计数据的正常天气、恶劣天气出现的概率。其中λavg=0.5，Fb=0.6，Pn=0.9，Pa=0.1。

根据泊松分布，从t0时刻开始正常运行的元件在t0+Δt时刻发生停运的概率可以近似表达为

式中:λi为元件的故障率;Δt为时间间隔，可以取为15 min或1 h。

因此，在t0+Δt时刻某一预想事故发生的概率可以由下式计算:

式中:E为预想事故下的系统状态;D、U分别为该系统状态下故障元件集合和正常元件集合;pi、pj分别为元件i、j的故障概率。

2.2 well-being风险贡献度指标

well-being模型根据确定性准则(N-1)将系统分为3种状态［21］:安全状态、警戒状态、紧急状态。风险追踪方法［11］利用风险权重分配的原理，将该系统状态下的风险值按贡献大小分配给各个失效设备，追踪电力系统风险到设备级。文献［12］将风险追踪模型融入到well-being模型中，提出了well-being风险追踪模型，并定义了设备警戒贡献度和紧急贡献度指标，能够追踪系统风险到各个设备，量化设备对系统运行风险贡献的大小。

对于规模较大的系统，采用枚举法［12］枚举所有

的系统状态，在计算上过于繁琐，因此本文采用非序贯蒙特卡洛法进行系统状态选取，形成预想故障集［22］。根据well-being分析准则，选取某一预想故障的系统状态k后，进行连通性分析和直流潮流分析以及“N-1”校验，确定该系统状态的类别(安全、警戒或紧急)，剔除安全状态后，根据式(6)计算该状态下的系统警戒状态概率PkAC和系统紧急状态概率为

式中SA、SE分别为预想故障集中的警戒状态集合和紧急状态集合。

得到系统状态概率后，运用风险追踪方法，依次遍历预想故障集的所有故障，可得到元件警戒贡献度和紧急贡献度，即

系统中某些元件的故障容易受到其他元件故障的影响，为了表征这些元件对其他元件故障的敏感程度，引入元件敏感度指标来修正元件贡献度指标:

式中:N表示非序贯蒙特卡洛法选取的系统状态总数;Nb表示在整个过程中该元件受其他元件故障影响导致自身状态量(电压、电流等)偏离正常水平的总次数。

警戒贡献度和紧急贡献度，二者各有侧重也互相包含，为了充分反映well-being风险对系统状态的影响，综合警戒贡献度和紧急贡献度定义了well-being风险贡献度:

式中:Wi为系统元件的well-being风险贡献度;k1、k2为权值，满足关系k1+k2=1。

k1k2的取值可根据警戒贡献度和紧急贡献度的严重程度而定，一般认为紧急状态的严重程度大于系统警戒状态，所以 k2取值一般大于 k1，本文k1取值0.2，k2取值 0.8。

3 线路脆弱性评估方法

3.1 综合脆弱性评估指标

电网是一个复杂且紧密联系的系统，线路开断存在着相互制约的关系，well-being风险贡献度就从整体上量化了这种制约关系。同时，线路在电网中所处的位置也是不容忽略的因素，其是电网固有属性的一种体现，而线路介数量化了线路在电网中位置的关键程度。线路脆弱性评估必须全面考虑各类影响因子的影响，建立综合评价指标。本文结合线路介数和well-being风险贡献度，构造了综合脆弱性指标Vli，定义为

式中ω1、ω2分别为归一化的线路介数指标Bli和wellbeing风险贡献度指标Wli在综合脆弱性指标Vli中所占的权值，满足关系ω1+ω2=1。

ω1、ω2的取值可根据线路脆弱性计算的实际需求而定，当计算结果侧重于对电网自身结构的考察时，可以使ω1的取值大于ω2;若侧重于对电网运行状态，尤其是元件故障对系统整体状态的影响程度的考察时，可以使ω1的取值小于ω2。如果认为电网结构和电网运行状态的影响程度同等重要，可以使ω1、ω2取值相等，本文ω1、ω2同时取为0.5。

由于线路加权介数Bi和well-being风险贡献度Wi的数量级和物理意义都不同，对二者的数值做归一化处理，消除不同量纲的影响，归一化指标为Bli和Wli。

式中Bmax和Bmin分别为所有线路介数指标的最大值和最小值。

式中Wmax和Wmin分别为所有线路well-being风险贡献度指标的最大值和最小值。

线路的综合脆弱性指标越高，表明该线路在电网中的地位越重要，移除该线路对系统带来的影响程度也就越严重。综合脆弱性指标弥补了单纯从网络结构或者网络状态进行评估的片面性，更具有实用性。

3.2 综合脆弱性评估方法流程

基于综合脆弱性指标，提出了输电线路脆弱性评估方法，遴选电网的脆弱线路，具体流程见图1。

图1 方法流程Fig.1 Flow chart of proposed method

(1)输入原始数据和模型参数，主要包括拓扑参数等。

(2)根据获取的气象信息，利用两状态天气模型计算系统元件实时故障概率。

(3)使用非序贯蒙特卡洛法选取系统状态，形成预想故障事件，并计算该预想故障事件发生的概率，设定最大抽样次数N=40 000。

(4)对某一选取的系统状态，基于线路加权介数模型，利用式(1)计算线路加权介数，并进行归一化。

(5)对某一选取的系统状态，基于well-being风险追踪模型，利用式(10)计算元件well-being风险贡献度，并进行归一化。

(6)利用归一化的指标计算综合脆弱性指标。

(7)遍历所有状态，如果状态选取完全，进入步骤(8)，否则返回步骤(4)。

(8)输出综合脆弱性指标并进行线路脆弱性评估和排序，辨识出系统的脆弱线路。

4 算例分析

本文以IEEE-RTS系统为例，验证提出的线路脆弱性评估方法的有效性。IEEE-RTS系统具体系统参数和元件故障率数据见文献［23］，接线如图2所示，根据230 kV和138 kV这2个电压等级将系统划分为区域1和区域2。

图2 IEEE-RTS系统Fig.2 IEEE-RTS system

为了评估天气因素对系统综合脆弱性的影响，对恶劣天气的时空转移进行更好地模拟，设置了2个场景。场景1:某日区域1和区域2的天气均为正常天气。场景2:某日00:00～12:00区域1内天气恶劣，区域2内天气正常;随后恶劣天气转移，13:00～24:00区域1内天气正常，区域2内天气恶劣。

(1)在场景1和场景2条件下，按综合脆弱性指标计算公式和相应评估流程，计算各条线路对应的综合脆弱性指标Vli并从高到低排序，结果见表1。

场景 1的评估结果中，线路14－16、11－14、11－13、15－24的综合脆弱性指标值最高，排序最为靠前。从拓扑图中可以看出，这些线路处于重要的输电通道上，是电源区到负荷区的重要联络线，构成了重要的输电断面，电能输送任务繁重，如果发生故障将严重阻碍电能传输，导致系统性风险水平大幅上升。这些位于重要输电断面上的线路在网架结构中处于较关键的位置，线路介数较大，一旦断开，系统进入警戒状态或者紧急状态的概率大大增加，对系统的well-being风险贡献度较高。综合脆弱性评估方法不仅能够识别出处于关键位置的脆弱线路，更重要的是通过wellbeing风险贡献度量化了线路对系统状态的影响程度，在脆弱性评估中增加了概率特性。

87

表1 种场景下线路脆弱性对比Table 1 Comparison of line vulnerability indicators under two scenarios

综合场景1和场景2的评估结果，线路14－16、11－14在2种场景下的脆弱性排序都位于前2位，属于极端脆弱线路。这2条线路构成了中部输电通道，断开会使得左右两边输电通道的潮流同时增大，系统well-being风险水平急剧升高;其线路介数和well-being风险贡献度指标都较大，故障会从网络结构和网络状态2个层面对系统造成不利影响，导致系统的能量输送受到重大影响，属于需要密切关注的关键线路。

(2)在场景1条件下，本文的综合脆弱性评估方法与文献［24］的对比结果见表2，同时通过查询文献［23］中的线路故障率数据，将各线路的故障率也列于表中。

表2 不同方法线路综合脆弱性指标对比Table 2 Comparison of line comprehensive vulnerability indicators in different methods

由表2可以看出，线路3－24、6－10、15－24在文献［24］与本文的评估结果中的线路脆弱性指标都排在前列，属于脆弱性较高的关键线路，2种方法得出了类似结果。不同的是，文献［24］的评估结果中最为脆弱的线路是230 kV电网与138 kV电网的联络通道，而本文方法的评估结果中，电源区到负荷区的重要联络线脆弱性最高。对比线路故障率数据可以发现，230 kV电网与138 kV电网的联络线路的故障率仅为0.02次/a，这些线路在设计上属于高可靠性线路，故障概率极小，而电源区到负荷区的输电断面上的线路的故障率接近0.4次/a，约为其20倍，发生故障的可能性大大增加，而且一旦发生故障将导致系统的拓扑结构和系统状态发生较大变化，其脆弱性更高更为合理。

(3)所有线路脆弱性指标结果见图3，图中用虚线将整个图分成2块，左侧表示区域1内线路，右侧表示区域2内线路。

图3 线路脆弱性指标Fig.3 Line vulnerability indicator

由图3可以看出，区域1天气恶劣时，线路综合脆弱度取值明显升高，结合表1中场景2的评估结果，区域1内天气恶劣时，线路6－10、2－6、3－9等的综合脆弱性都排入前10位，恶劣天气对线路运行状态有显著影响，导致区域1内线路脆弱性指标明显升高。区域2天气恶劣时，排在前列的线路和正常天气排序基本一致，但区域2内线路的总体排序较场景1更为靠前，且排序靠前线路的综合脆弱性指标略有增大。输电线路运行期间遭遇恶劣天气，会导致故障率增大，脆弱性高的线路更易发生故障，进而影响整个系统的正常运行，说明线路脆弱性评估考虑天气因素尤其是恶劣天气的影响是非常必要的。

(4)将所有线路的综合脆弱性指标值按降序排列后绘制于图4中，图中横坐标表示输电线路按综合脆弱性大小排序之后的降序线路序号。

图4 线路脆弱性指标排序Fig.4 Sorting of line vulnerability indicator

由图4可以看出，在各场景评估结果中，综合脆弱性指标低于0.3的输电线路占输电线路总数的80%之多，排在前列的线路其综合脆弱性指标是排序靠后线路的2至4倍，说明电网中只有少部分线路的脆弱值较高，发生故障会对电网的功能产生较大影响，大部分线路显示出相对较低的脆弱性。因此加强对少部分脆弱性较高的线路的监控，可以显著提高电网的安全稳定运行水平。

结合了线路介数和well-being风险贡献度的电网脆弱性评估方法有效克服了以往从单一角度去评估电网脆弱性的弊端，提高了辨识精度和辨识效果，而且采用well-being风险贡献度进行状态评估可以将概率性风险分析融入脆弱性评估中，反映天气因素对线路故障率的影响，增强风险分析的实用性，对电网监控更有实际意义。

5 结论

(1)电网脆弱性较大的线路往往位于重要输电通道和输电断面上，这些线路的正常运行关系着电网的安全稳定性，属于电网中的关键线路。电网中只有少部分线路的脆弱性值较高，大部分线路显示出相对较低的脆弱性，这些脆弱性较高的线路是电网中最为关键的线路，需要密切监视其运行状态，以提高电网安全运行水平。

(2)综合脆弱性指标可以从网架结构和网络运行状态角度评估线路脆弱性，克服了从单一角度评估的片面性，使评估结果更加全面和合理。

(3)恶劣天气会使所在区域内的线路脆弱性整体升高，线路脆弱性评估中考虑恶劣天气的影响，可以使评估结果更加符合实际运行条件。

［1］毛安家，张戈力，吕跃春，等.2011年9月8日美墨大停电事故的分析及其对我国电力调度运行管理的启示［J］．电网技术，2012，36(4):74-78．Mao Anjia，Zhang Geli，Lü Yuechun，et al．Analysis on large-scale blackout occurred in south America and north Mexico interconnected power grid on Sept.8，2011 and lessonsforelectric power dispatching in China［J］．Power System Technology，2012，36(4):74-78．

［2］曾鸣，李娜，董军，等．基于大安全观的电网运行管理关键技术:关于印度大停电的思考［J］．电力系统自动化，2012，36(16):9-13．Zeng Ming，Li Na，Dong Jun，et al．Key technologies of power grid operation and management based on philosophy of general security:a view of blackout in India［J］．Automation of Electrical Power Systems，2012，36(16):9-13．

［3］Vaiman M，Bell K，Chen Y，et al．Risk assessment of cascading outages:methodologies and challenges［J］．IEEE Transactions on Power Systems，2012，27(2):631-641．

［4］ Motter A E，Lai Y C．Cascade-based attacks on complex networks［J］．Physical Review E，2002，66(2):1-4．

［5］倪向萍，梅生伟，张雪敏．基于复杂网络理论的输电线路脆弱度评估方法［J］．电力系统自动化，2008，32(4):1-5．Ni Xiangping，Mei Shengwei，Zhang Xuemin．Transmission lines vulnerability assessment based on complex network theory［J］．Automation of Electric Power Systems，2008，32(4):1-5．

［6］陈晓刚，孙可，曹一家．基于复杂网络理论的大电网结构脆弱性分析［J］．电工技术学报，2007，22(10):138-144．Chen Xiaogang，Sun Ke，Cao Yijia．Structural vulnerability analysis of large power grid based on complex network theory［J］．Transactions of China Electrotechnical Society，2007，22(10):138-144．

［7］孟仲伟，鲁宗相，宋靖雁．中美电网的小世界拓扑模型比较分析［J］．电力系统自动化，2004，28(15):21-24，29．Meng Zhongwei，Lu Zongxiang，Song Jingyan．Comparison analysis of the small-world topological model of Chinese and American power grids［J］．Automation of Electric Power Systems，2004，28(15):21-24，29．

［8］曹一家，陈晓钢，孙可．基于复杂网络理论的大型电力系统脆弱线路识别［J］．电力自动化设备，2006，26(12):1-5．Cao Yijia，Chen Xiaogang，Sun Ke．Identification of vulnerable lines in power grid based on complex network theory［J］．Electric Power Automation Equipment，2006，26(12):1-5．

［9］丁明，韩平平．基于小世界拓扑模型的大型电网脆弱性评估［J］．中国电机工程学报，2005，25(S):118-122．Ding Ming，Han Pingping．Small-world topological model based vulnerability assessment to large-scale power grid［J］．Proceedings of the CSEE，2005，25(supplements):118-122．

［10］Xie K，Billinton R．Tracing the unreliability and recognizing the major unreliability contribution ofnetwork components［J］．Reliability Engineering and System Safety，2009，94(5):927-931．

［11］Xie K，Hu B，KarkiR．Tracing thecomponentunreliability contributions and recognizing the weak parts of a bulk power system［J］．European Transactions on Electrical Power，2011，21(1):254-262．

［12］邓彬，郭创新，王越，等．基于well-being分析的电网设备重要度评估与排序方法［J］．电网技术，2013，37(12):3489-3496．Deng Bin，Guo Chuangxin，Wang yue，et al．An Assessment and Ranking Method for Component Importance Based on Well-being Analysis［J］．PowerSystem Technology，2013，37(12):3489-3496．

［13］魏震波，刘俊勇，朱国俊，等．基于电网状态与结构的综合脆弱评估模型［J］．电力系统自动化，2009，33(8):11-14．Wei Zhenbo，Liu Junyong，Zhu Guojun，et al．A new integrative vulnerability evaluation model to power grid based on running state and structure［J］．Automation of Electric Power Systems，2009，33(8):11-14．

［14］韩泽文，苏永清，岳继光，等．电网脆弱性综合指标建立与评估［J］．电力建设，2015，36(8):89-94．Han Zewen，Su Yongqing，Yue Jiguang，et al．Establishment and assessment of power grid vulnerability comprehensive index［J］．Electric Power Construction，2015，36(8):89-94．

［15］吴莹燕，林韩，温步瀛，等．考虑电网状态和网络结构的脆弱线路评估［J］．华东电力，2013，41(3):519-523．Wu Yingyan，Lin Han，Wen Buying，et al．Vulnerable Line Evaluation Considering Power Grid Running State and Structure［J］．East China Electric，2013，41(3):519-523．

［16］蔡晔，曹一家，李勇，等．考虑电压等级和运行状态的电网脆弱线路辨识［J］．中国电机工程学报，2014，34(13):2124-2131．Cai Ye，Cao Yijia，Li Yong，et al．Identification of Vulnerable Lines in Urban Power Grid Based on Voltage Grade and Running State［J］．Proceedings of the CSEE，2014，34(13):2124-2131．

［17］何俊，庞松龄，禹冰，等．基于容量介数指标的电网脆弱线路识别［J］．电力系统保护与控制，2013，41(6):30-35．He Jun，Pang Songling，Yu Bing，et al．Vulnerable line identification of power grid based on capacity betweenness index［J］．Power System Protection and Control，2013，41(6):30-35．

［18］丁明，韩平平．加权拓扑模型下的小世界电网脆弱性评估［J］．中国电机工程学报，2008，28(10):20-25．Ding Ming，Han Pingping．Vulnerability assessment to small-world power grid based on weighted topological model［J］．Proceedings of the CSEE，2008，28(10):20-25．

［19］刘耀年，术茜，康科飞，等．基于电抗加权介数指标的电网脆弱线路识别［J］．电力系统保护与控制，2011，39(23):89-92．Liu Yaonian，Zhu Xi，Kang Kefei，et al．Identification of vulnerable lines in power grid based on the weighted reactance betweenness index［J］．Power System Protection and Control，2011，39(23):89-92．

［20］何剑，程林，孙元章，等．条件相依的输变电设备短期可靠性模型［J］．中国电机工程学报，2009，29(7):39-46．He Jian，Cheng Lin，Sun Yuanzhang，et al．Condition dependent short-term reliability modelsoftransmission equipment［J］．Proceedings of the CSEE，2009，29(7):39-46．

［21］Billinton R，Karki R．Application of Monte Carlo simulation to generating system well-being analysis［J］．IEEE Transactions on Power Systems，1999，14(3):1172-1177．

［22］李文沅．电力系统风险评估模型、方法和应用［M］．北京:科学出版社，2005:70-73．

［23］Subcommittee P M．IEEE reliability testsystem ［J］．IEEE Transactions onPowerApparatusand Systems，1979(6):2047-2054．

［24］王志强，李欣，李岩，等．基于复杂网络与风险的电网综合脆弱性评估［J］．现代电力，2014，35(3):49-55．Wang Zhiqiang，Li Xin，Li Yan，et al．Comprehensive vulnerability evaluation of power grid based on complex network and risk theory［J］．Modern Electric Power，2014，35(3):49-55．