计及配电网经济性与可靠性的电池储能系统优化配置

刘芳，李冰，张帆

(国网冀北电力有限公司经济技术研究院，北京市100045)

0 引言

随着新能源技术的发展，低碳经济的要求以及国家政策的大力支持，分布式电源(distribution generation，DG)正被越来越多的电力用户所重视和采用，未来将会有大量DG接入配电网，给配电网的安全可靠运行带来巨大挑战。在配电网中合理配置储能系统是解决该问题的有效措施之一［1］。

目前，国内外学者已对配电网中储能系统的优化配置问题进行了深入研究。研究主要从2个角度出发，一是从储能系统的配置提高配电网性能指标的角度，探讨储能系统优化配置的可行性，如提高电压质量、削峰填谷、平抑分布式电源出力波动或降损等方面［2-5］。文献［2］以提高电网电压稳定性和降损效益为目标，建立了配电网中电池储能系统(battery energystoragesystem，BESS)与分布式光伏(photovoltaic，PV)发电的协同优化配置模型，并提出了一种新的自适应算法解决该多目标优化配置问题。文献［3］针对DG接入区域配电网对负荷特性的负面影响，以“削峰填谷”和“平滑负荷”分别作为负荷控制目标，并结合储能系统的成本进行优化，探讨了不同策略下“削峰填谷”的效果。文献［4］从混合储能系统可有效降低风电功率波动对电网影响的角度出发，在有效分解风电有功功率的基础上，确定了满足电池及超级电容器混合储能系统技术要求及工程指标的配置方案。文献［5］以钠硫电池为例，对BESS进行了建模及计算仿真，使用潮流法进行了配电网的线损计算。算例结果表明在配电网络的合理位置接入合理容量的储能电池，并考虑电池本身的加热损耗，可有效降低线损率。二是从经济性角度出发，考虑配置储能系统全寿命周期成本，详细探讨储能系统接入后给配电网带来的实际收益与潜在收益，包括低储高发套利、政府电价补贴、延缓电网升级、网络降损效益、环境效益等［6-7］。

由上述研究可知，目前储能系统的优化配置并未过多考虑对电网可靠性的影响，仅在约束条件中考虑电网的“N－1”要求。基于此，本文首先提出一种含BESS及DG的配电网可靠性简化计算方法，该方法旨在量化BESS加入后对配电系统可靠性提高的贡献，并不直接求解出配电网可靠性指标的精确值。然后，建立计及配电网经济性与可靠性的电池储能系统优化配置模型。以BESS配置后配电网的年净收益，系统故障状态下BESS持续供电电量及持续供电时间最大为目标，并采用改进的传统强度帕累托优化算法(improved strength Pareto evolutionary algorithm，ISPEA)求解该多目标优化配置问题的帕累托前沿。最后对IEEE-33节点配电系统进行仿真计算，验证所建模型的可行性及有效性。

1 含BESS及DG的配电网可靠性简化计算方法

储能装置作为能量有限元件，其任意时刻的荷电状态(state of charge，SOC)高度依赖于自身所经历的历史状态，因此，对含储能元件的系统进行准确的可靠性评估必须依托能够反映系统时序特点的算法。文献［8］在分析并网储能系统物理结构的基础上，运用状态空间法建立了BESS的可靠性模型，并利用蒙特卡洛模拟法进行了含BESS配电系统的可靠性评估。为了改进传统序贯蒙特卡洛模拟法计算效率低的缺点，文献［9］采用了改进的伪时序状态转移抽样方法对含储能电力系统的可靠性指标进行了定量计算。

对含储能元件的电力系统进行可靠性评估，研究难点在于简化计算过程，提高计算效率。在含DG的配电网中进行储能系统优化配置的过程中考虑可靠性，仅需比较不同储能配置方案下系统可靠性的优劣，无须计算出精确的系统可靠性指标。基于此，为了简化计算过程，进一步缩短计算时间，本文提出了一种含储能系统配电网可靠性的简化计算方法。

1.1 馈线区域划分

本文参考文献［10］中含分布式“风光蓄”的配电网馈线分区方法，从系统非电源元件发生故障前后，储能系统是否对系统的可靠性作出贡献的角度出发，以断路器开关为界划分馈线区域，如图1所示。位于同一馈线区域的元件发生故障后，储能系统供电状况相同，包括是否继续为断电负荷供电以及储能系统的最大持续供电时间。

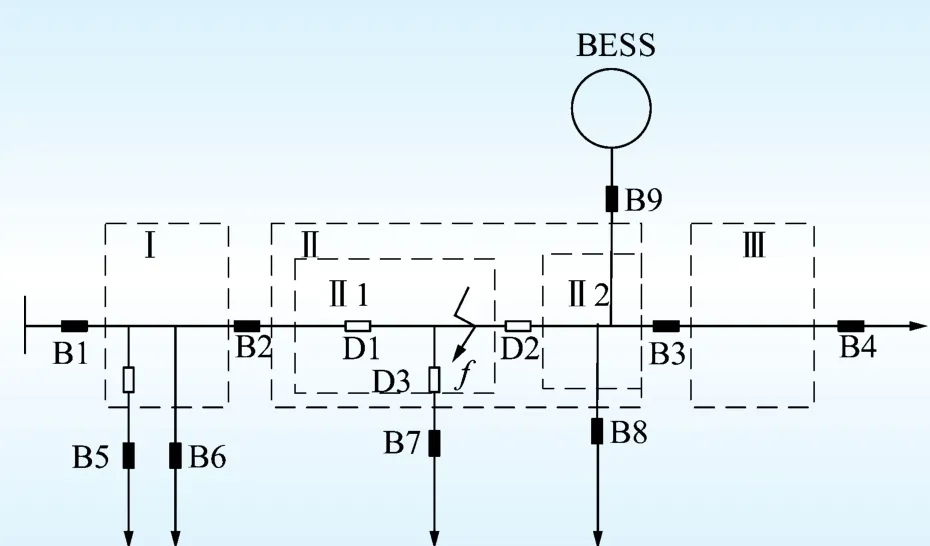
图1 馈线区域划分示意图Fig.1 Feeder region partition

该配电网馈线分为3个区域(区域Ⅰ/Ⅱ/Ⅲ)，其中储能系统所在区域又进一步划分为2个区域，即以断路器和隔离开关为界，储能系统所在线路为一区域(区域Ⅱ2)，区域Ⅱ中其余线路为另一区域(区域Ⅱ1)。

区域Ⅰ:该区域非电源元件发生故障后，断路器B1、B2、B5、B6断开，B2下游线路以孤岛模式运行，孤岛运行时间为故障修复时间。此时，在储能系统SOC满足约束的前提下，可以继续为部分负荷供电，

77对系统的可靠性提高有贡献。

区域Ⅱ1:该区域非电源元件发生故障后，断路器B2、B3、B7、B8、B9 先行断开，故障隔离后，在储能系统SOC满足约束的前提下，可以继续为部分负荷供电。例如，图中f点处发生故障后，上述断路器首先断开，此时储能系统不能对负荷继续供电，故障隔离后，即分段开关D1、D2、D3断开后，断路器闭合，此时分段开关D2下游的线路以孤岛模式运行，储能系统继续为部分负荷供电，对系统可靠性提高有贡献，最大持续供电时间为故障修复时间减去故障隔离时间。

区域Ⅱ2:该区域非电源元件发生故障后，断路器断开情况与区域Ⅱ1相同。故障隔离后，分段开关D2上游区域正常并网运行，断路器B3下游区域运行于孤岛状态。但由于储能系统与故障点位于同一区域，不能继续为负荷供电，对系统的可靠性提高无贡献。

区域Ⅲ:该区域非电源元件发生故障后，断路器B3、B4断开，储能系统所在区域不受影响，正常并网运行，因此储能系统对提高系统可靠性无贡献。

1.2 系统元件建模

1.2.1 非电源元件模型

系统中所有的非电源元件，包括配电变压器、断路器、隔离开关、线路等看作可修复元件，沿用经典的两状态马尔科夫模型，其参数为故障率λ和修复率μ。

1.2.2 DG系统

在不考虑上级系统容量限制的情况下，只有系统内非电源元件停运时，用户才会出现停电风险，储能系统才有可能对系统的可靠性提高作出贡献。因此，在计算加入BESS后配电系统可靠性改善情况时，不考虑DG及BESS的停运情况。

本文DG考虑分布式光伏发电，其出力主要与电池板上接收的太阳光辐射强度有关，建模如下［11］。

式中:S为光伏电池板的有效面积;I(t)为t时刻电池板接收到的光强;ηPV为太阳能电源板的转换效率;Kc为阈值常数。

I(t)等于一个由太阳辐射角确定的基础强度Id(t)叠加上一个随机分量ΔI(t)。Id(t)是与时刻t有关的二次函数，ΔI(t)服从正态分布，具体公式见文献［11］。

1.2.3 储能系统

储能系统无故障并网运行状态下的充放电功率为本文的决策变量之一。充放电功率及荷电状态满足式(2)中所列各等式和不等式约束:

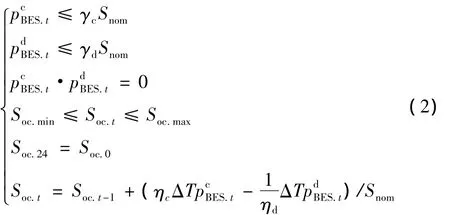
孤岛运行状态下，储能电池的充放电功率主要由孤岛内的净交换功率pex决定，满足式(3);当pex为正时，储能充电且充电功率满足式(4);当pex为负时，储能放电且放电功率满足式(5)。

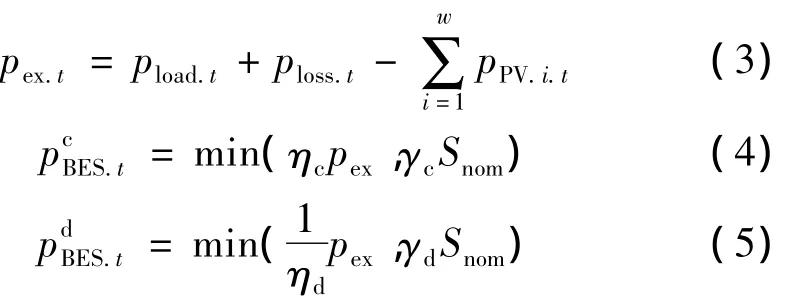
式中:pload．t，ploss．t，pPV．i．t分别为 t时刻孤岛内的负荷功率，孤岛网损功率以及PV上网功率;w为与BESS处于同一孤岛的PV的总数量。

1.3 评估流程

步骤一:输入系统网络结构及DG和BESS的位置和容量，根据1.1节馈线分区方法，由计算机自动遍历所有非电源元件的馈线区域并进行划分。设定系统总模拟时间为T，故障隔离时间为0.5 h。

步骤二:搜索变电站到BESS接入点的最小路径，分别记录区域Ⅰ和区域Ⅱ中位于最小路径上的非电源元件集合NuⅠ和NuⅡ。

步骤三:按式(6)分别对区域Ⅰ及区域Ⅱ1的故障修复时间进行蒙特卡洛抽样，并抽样故障的起始时刻，根据式(1)计算获得该时刻各PV的出力情况，根据优化所得储能系统正常运行状态时的运行策略抽样该时刻的SOC值。

式中:μⅠ(Ⅱ)为区域Ⅰ或区域Ⅱ1的总修复率，计算公式如式(7)所示;R为在(0，1)区间服从均匀分布的随机数。

式中λiμi分别指元件i的故障率和修复率。

步骤四:采用文献［10］中的启发式算法，计算故障修复期间可以由BESS继续供电的负荷电量EBES及供电时间TBES。

步骤五:计算总模拟时间。分别累加抽样得到的2个区域的故障时间，按式(8)、(9)计算抽样总时间。判断TⅠ+TⅡ＜T是否成立，若是，则返回步骤二，继续进行故障抽样;若否，则执行下一步。

式中:TtolTTR．Ⅰ(Ⅱ)为区域Ⅰ或区域Ⅱ1的总故障时间;TⅠ(Ⅱ)为区域Ⅰ或区域Ⅱ1 的总模拟时间;λⅠ(Ⅱ)为区域Ⅰ或区域Ⅱ1的总故障率，计算公式如式(10)所示。

步骤六:根据BESS处于孤岛期间的持续供电电量EBES及供电时间TBES，计算该储能配置方案在总模拟时间里的平均持续供电量及平均持续供电时间。

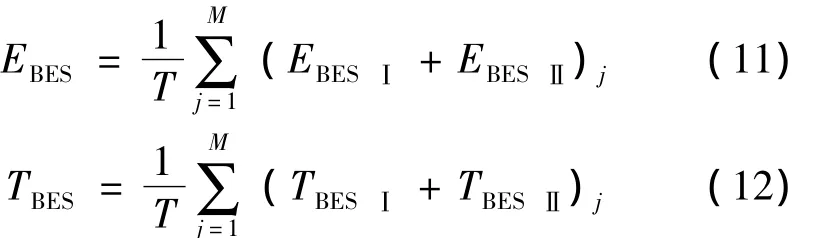
式中M为故障总抽样次数。

2 经济效益分析

由于目前国内对储能并没有明确的补偿政策，并且储能系统接入电力系统的潜在效益，如延缓电网投资、提供辅助服务、环境效益等，在目前国内电力市场环境下暂时无法直接量化为经济效益。因此，本文仅考虑目前电力市场环境下可以直接量化的收益和成本，如图2所示。

图2 配电网运营商成本—效益分析Fig.2 Cost-benefit analysis of DSO

在现行市场体制下，从运行成本的角度来看，对于配电网运营商(distribution system operator，DSO)，收益主要为向用户供电的售电收入;成本费用包括向上级电网的购电成本、向用户自建PV的购电成本以及投资建设储能系统的各项成本。

含DG的配电网中配置BESS的年净收益表示如下:

式中:T为BESS年利用小时数，本文取8 760;N为系统中总用户数;D为配电网系统中用户自建DG的数目;ps．n．t，pg．t，pdg．d．t，分别为 t时刻配电网为用户提供的售电功率，向上级电网的购电功率，DG上网功率，各项所乘系数分别为其对应的单位价格;CBESS为BESS的全寿命周期成本。

目前，BESS全寿命周期成本由一次性建设成本及运行维护成本组成，其中一次性建设成本通常分为能量成本与功率成本［7-8］。考虑资金的时间价值，为统一式(13)中各项时间尺度，将BESS一次性建设投资的现值转化成等年值，即

式中:cs指储能电池的单位容量成本;cp为储能电池的单位功率成本;β是投运至目标年的运行维护费用折算为初期投资费用的折算系数;τbat为储能电池的使用年限;r0为贴现率;Pnom为储能系统额定配置功率。

τbat的确定应考虑到电池的老化过程，老化过程和电池的放电深度有关。电池的健康状态(state of health，SOH)表示为式(15)［12］，即SOH(t)=Snom(t)/Sref．nom(15)式中Sref．nom代表储能电池的额定参考容量，由电池生产商的生产数据手册提供。

由INES协会的试验数据可知，电池的老化程度与放电深度基本呈线性关系，并且在文献［13］中给出了不同类型电池的线性老化系数ϑ。当电池处于放电状态时，考虑老化因素的电池容量由式(16)、(17)计算可得:

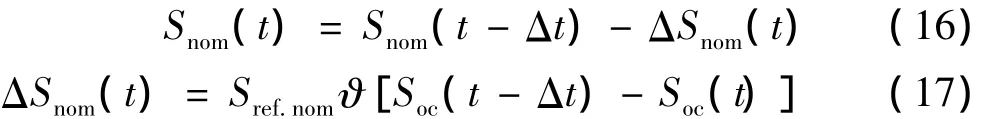
联立式(16)和(17)可得:

当SOH(t)小于某一数值时，电池将不能正常工作，此时对应的运行时间设为Top。则

式中τbat．sl表示储能电池的质保期(a)，可由电池生产商的生产数据手册提供。

3 考虑经济性与可靠性的BESS优化配置模型

本文考虑经济性与可靠性的BESS多目标优化配置模型表示如下:

maxF= ［maxf，maxEBES，maxTBES］ (20)式中:f表示配置BESS后配电网年净收益;EBES表示系统故障状态下BESS的持续供电电量;TBES表示系统故障状态下BESS的持续供电时间。模型决策变量为BESS的额定容量和额定功率及每时刻充放电功率。

除满足储能的技术条件约束式(2)外，还应满足系统安全稳定运行约束。

(1)系统有功功率平衡约束。

式中:pBES．t为t时刻储能系统的总出力(充电时为负值，放电时为正值);ploss．t表示系统的网络损耗。

(2)节点电压约束。

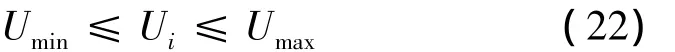
式中:Ui为节点i处的电压值;Umin及Umax分别为节点电压下限与电压上限。

(3)线路过负荷约束。

式中:Iij为节点i与节点j之间线路上的电流;Iij．max为线路最大允许载流量。

(4)上级电网输入功率约束。

式中pgrid．max为配电网与上级电网交换功率的约束上限。

4 基于Pareto前沿的ISPEA算法

由经验可知，配置BESS的经济性与可靠性始终相互矛盾，无法同时达到最优。要实现求解本文所建的多目标优化模型，有效方法是寻找模型的Pareto前沿解。强度帕累托算法(strength pareto evolutionary algorithm，SPEA)可对具有多个冲突目标的问题进行寻优，且不需转化子目标函数，是处理多目标问题的有效方法［14］。本文采用文献［14］中提出的改进的SPEA算法对该多目标优化模型进行求解，具体步骤如图3所示。

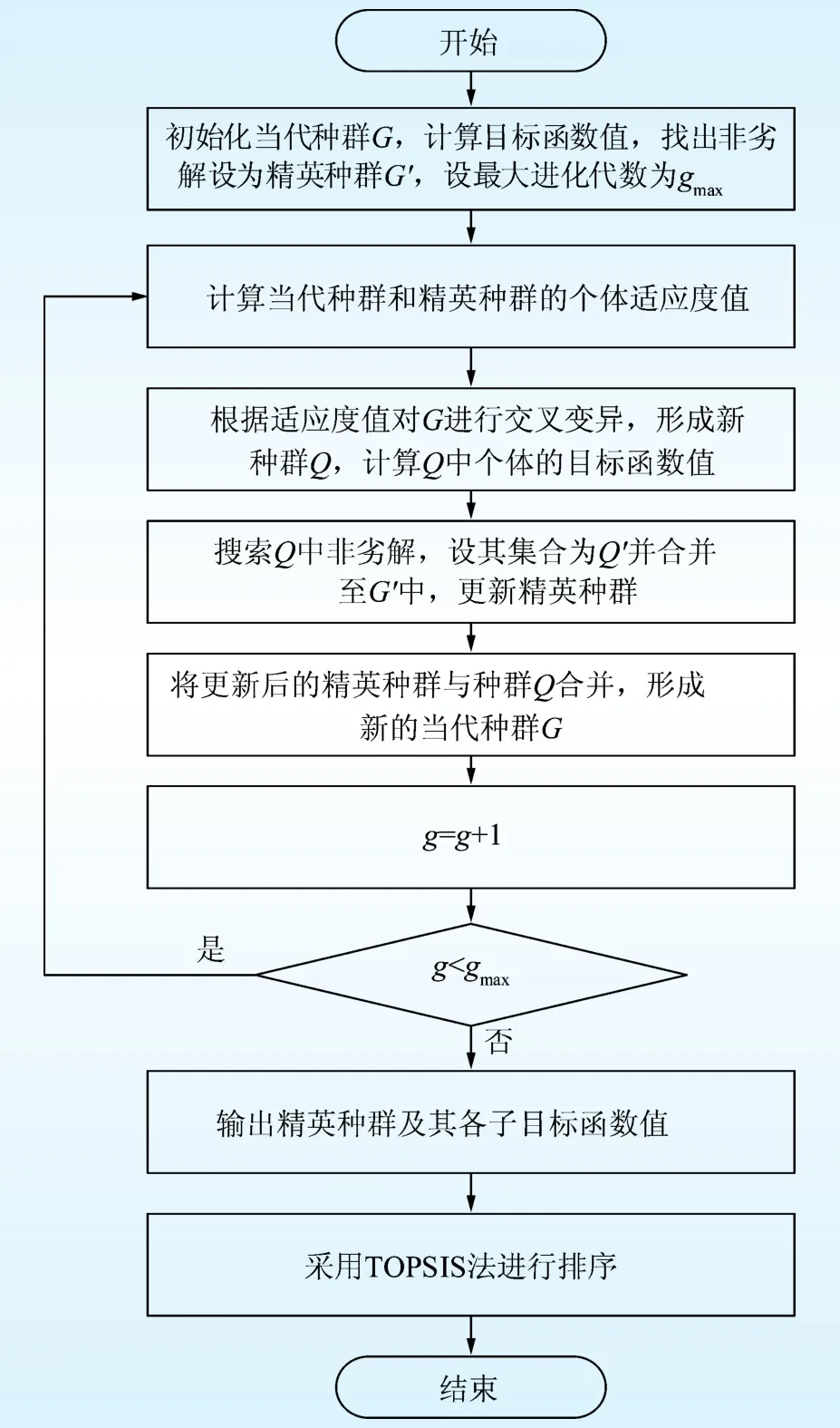
图3 ISPEA流程Fig.3 Flow chart of ISPEA

5 算例分析

本文以IEEE-33节点的配电网测试系统为例进行仿真，验证本文模型与算法的有效性。网络总负荷为3 715 kW+j230 0 kvar［15］。网络结构及用户自建PV的情况如图4所示，其中灰色放大节点为自建PV的用户，标注数字为PV的额定功率。PV上网电价取值为0.42元/(kW·h)。

图4 改进的IEEE-33节点配电网系统Fig.4 Modified IEEE-33 nodes distribution system

系统典型负荷曲线如图5中实线所示［16］，由基础光照强度决定的PV出力如图5中虚线所示。

图5 典型日负荷及光伏出力曲线Fig.5 Typical daily load and PV output curve

配电网向上级电网购电电价、配电网售电电价及系统各元件的故障率和修复率等参数设置参见附录。其余系统所需参数如表1所示。

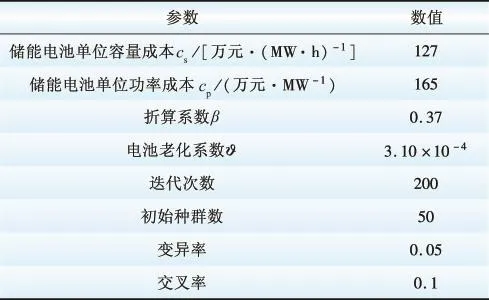
表1 仿真参数设置Table 1 Simulation parameters setting

以BESS配置在节点11处为例，采用本文所建模型及优化方法进行求解，选取TOPSIS排名前10的Pareto前沿解，结果分布如图6所示。在实际应用中，运行人员可以根据对经济性和可靠性侧重点的不同，在前沿解中灵活选取储能系统的配置方案。

图6 Pareto前沿解空间分布情况Fig.6 Distribution of Pareto front

由图6可知，随着年净收益f的提高，持续供电电量EBES和持续供电时间TBES优化值都呈下降趋势，这是由于目前BESS单位配置成本较高，若不考虑其给配电网带来的潜在效益，DSO投资建设BESS将处于负盈利状态，因此随着年净收益的提高，配置BESS的额定容量及额定功率减小，导致电网发生故障时BESS可用电量减小，从而使EBES及TBES下降。

为进一步对比分析，选取TOPSIS排名第1的Pareto前沿解方案，对比分别以经济性和可靠性为优化目标进行单目标优化的结果，并列出无储能系统时(初始方案)的计算结果，如表2所示。

表2 不同优化目标下优化结果对比Table 2 Optimization results comparison in different objectives

由表2优化结果可知，当仅考虑经济性目标时，BESS的配置容量与额定功率都较小，相比于初始方案净收益虽有所提高，但提高幅度较小，这说明目前储能电池的单位配置成本较高，若不考虑BESS给配电网带来的潜在效益，则导致其在电力系统中大规模应用的经济性较差;当仅考虑可靠性目标时，虽然EBES及TBES有较大改善，但经济性很差;采用本文建立的多目标优化模型所得结果是各单目标优化结果的折衷，证明本文所建模型具有一定的可行性。但同时发现，采用本文模型配置BESS相比于系统BESS配置时配电网净收益下降，这说明现阶段通过配置BESS提高系统的可靠性是建立在牺牲经济性的基础之上的。

对于不同方案，1天内BESS荷电状态变化情况如图7所示(起始SOC均设为0.5)。

由图7可知，仅考虑可靠性指标时，BESS的SOC尽可能保持在最大值，为系统故障做后备。仅考虑经济性指标时，充放电状态与配电网趸购电价及系统负荷大小有关，以尽可能高储低发。而采用本文模型时，处于折衷状态，与预期结果相同。

为探究配电网中DG渗透率的不同对BESS配置结果的影响，在其他参数不变的基础上，逐渐改变配电网中PV的容量，在节点11处配置BESS的结果如表3所示(仅将每种情况下TOPSIS排名第1的Pareto前沿解列于表3)。

图7 不同优化目标时BESS的荷电状态Fig.7 SOC of BESS with different objectives

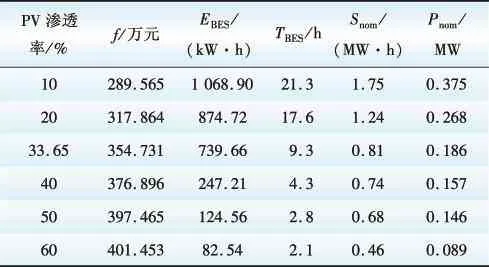
表3 不同PV渗透率下储能优化结果Table 3 Optimization results of BESS with different PV penetration

由表3可知，随着PV渗透率的提高，配电网的净收入逐渐增大，但增长幅度逐渐减小。这是由于随着PV渗透率的提高，储能容量和功率逐渐减小，因此配置成本逐渐减小，导致配电网净收益逐渐增大。但BESS容量过小时，不能充分发挥其减损效益及高储低发效益，本应导致配电网净收益降低，但本文所设光伏上网电价低于配电网向上级电网购电峰时电价(0.42元/(kW·h)＜0.440元/(kW·h))，而光伏出力又具有正负荷特性，因此光伏容量的增大可以减小配电网的购电电价。综上，两者相制衡，反映到配电网净收益上即为净收益增长速度变缓。BESS在系统故障期间的EBES及TBES逐渐减小，这是由于在BESS与光伏相对位置不变的情况下，系统故障时导致BESS与PV处于同一孤岛的概率不变，但随着配电网中PV容量的逐渐增大，光伏发电为停电用户持续供电的电量及供电时间逐渐提高，削弱了BESS在提高系统可靠性方面的作用。

6 结语

本文提出了一种含DG及储能系统的配电网可靠性评估的简便计算方法，量化储能配置后对配电网可靠性提高所做的贡献。在此基础上，建立了同时考虑经济性和可靠性的BESS优化配置方法，采用改进的强度帕累托算法求取其帕累托前沿。算例结果表明，目前储能电池单位造价较高，若要求储能配置后在一定程度上改善系统可靠性，则系统运行经济性会受损;提高配电网中DG的接入容量，一定程度上可以减小以经济性和可靠性为配置目标的BESS的需求容量和功率。

［1］唐文左，梁文举，崔荣，等．配电网中分布式储能系统的优化配置方法［J］．电力建设，2015，36(4):38-45．Tang Wenzuo，Liang Wenju，Cui Rong，et al．Optimal allocation method of distributed energy storage system in distribution network［J］．Electric Power Construction，2015，36(4):38-45．

［2］ Kabir M N，Mishra Y，Ledwich G，et al．Improving voltage profile of residential distribution systems using rooftop PVs and battery energy storage systems［J］．Applied Energy，2014(134):290-300．

［3］杨玉青，牛利勇，田立亭，等．考虑负荷优化控制的区域配电网储能配置［J］．电网技术，2015，39(4):1019-1025．Yang Yuqing，Niu Liyong，Tian Liting，et al．Configuration of energy storage devices in regional distribution network considering optimal load control［J］．Power System Technology，2015，39(4):1019-1025．

［4］马速良，马会萌，蒋小平，等．基于Bloch球面的量子遗传算法的混合储能系统容量配置［J］．中国电机工程学报，2015，35(3):592-599．Ma Suliang，Ma Huiyin，Jiang Xiaoping，et al．Capacity configuration of the hybrid energy storage system based on bloch spherical quantum genetic algorithm［J］．Proceedings of the CSEE，2015，35(3):592-599．

［5］姚遥，刘东，廖怀庆，等．含储能电池的配电网降损分析［J］．华东电力，2010，38(5):677-680．Yao Yao，Liu Dong，Liao Huaiqing，et al． Analysis on Loss Reduction of Distribution Network with Energy Storage Battery［J］．East China Electric Power，2010，38(5):677-680．

［6］颜志敏，王承民，郑健，等．配电网中蓄电池储能系统的价值评估模型［J］．电力自动化设备，2013，33(2):57-61．Yan Zhimin，Wang Chengmin，Zhen Jian，et al．Value assessment model of battery energy storage system in distribution network［J］．Electric Power Automation Equipment，2013，33(2):57-61．

［7］向育鹏，卫志农，孙国强，等．基于全寿命周期成本的配电网蓄电池储能系统的优化配置［J］．电网技术，2015，39(1):264-270．Xiang Yupeng，Wei Zhinong，Sun Guoqiang，et al．Life Cycle Cost Based Optimal Configuration of Battery Energy Storage System in Distribution Network［J］．Power System Technology，2015，39(1):264-270．

［8］钟宇峰，黄民翔，羌丁建．电池储能系统可靠性建模及其对配电系统可靠性的影响［J］．电力系统保护与控制，2013，41(19):95-102．Zhong Yufeng，Huang Minxiang，Qiang Dingjian．Reliability modeling of battery energy storage system and its effect on the reliability of distribution system［J］．Power System Protection and Control，2013，41(19):95-102．

［9］程林，常垚，刘满君，等．基于伪时序状态转移抽样法评估含储能电力系统可靠性［J］．电力系统自动化，2014，38(7):53-59．Cheng Lin，Chang Yao，Liu Manjun，et al．Reliability evaluation of energy storage integrated power system based on pseudo-sequential state transition sampling algorithm［J］．Automation of Electric Power Systems，2014，38(7):53-59．

［10］葛少云，王浩鸣，王源山，等．含分布式风光蓄的配电系统可靠性评估［J］．电力系统自动化，2012，36(5):16-23．Ge Shaoyun，Wang Haoming，Wang Yuanshan，et al．Reliability evaluation of distribution system including distributed wind turbines，photovoltaic arrays and batteries［J］．Automation of Electric Power Systems，2012，36(5):16-23．

［11］梁惠施，程林，刘思革．基于蒙特卡罗模拟的含微网配电网可靠性评估［J］．电网技术，2011，35(10):76-81．Liang Huishi，Cheng Lin，Liu Sige．Monte Carlo simulation based reliability evaluation of distribution system containing microgrids［J］．Power System Technology，2011，35(10):76-81．

［12］Riffonneau Y，Bacha S，Barruel F，et al．Optimal power flow management for grid connected PV systems with batteries［J］．Sustainable Energy，IEEE Transactions on，2011，2(3):309-320．

［13］Lemaire-Potteau E，Mattera F，Delaille A，et al．Assessment of storage ageing in different types of PV systems:technical and economical aspects［C］//23rd European Photovoltaic Solar Energy Conference．Valencia，Spain，2008:2765-2769．

［14］盛四清，范林涛，李兴，等．基于帕累托最优的配电网多目标规划［J］．电力系统自动化，2014，38(15):51-57．Sheng Siqing，Fan Lintao，Li Xing，et al．Multi-objective planning of distribution network based on Pareto optimality［J］．Automation of Electric Power Systems，2014，38(15):51-57．

［15］吴小刚，刘宗歧，田立亭，等．基于改进多目标粒子群算法的配电网储能选址定容［J］．电网技术，2014，38(12):3405-3411．Wu Xiaogang，Liu Zongqi，Tian Liting，et al．Energy storage device locating and sizing for distribution network based on improved multi-objective particle swarm optimizer［J］．PowerSystem technology，2014，38(12):3405-3411．