三余度迎角传感器可靠性分析及重构技术研究

张羽白，谢慧慈，余云鹏，李玉飞，胡秀军

（中航工业洪都，江西 南昌330024）

0 引 言

为保证系统可靠性满足设计要求，现有的电传飞行控制系统均采用了多余度配置方式。因迎角传感器的安装受在飞机上的布局和空间限制，如不能按照电传飞行控制系统的基本四余度进行配置，可采用三余度配置，并通过合理的余度管理决策保证系统可靠性。另外，迎角信号作为纵向控制的关键反馈信号，需要对其故障后的故障瞬态、飞机飞行品质和系统稳定性等进行分析，并设计迎角全故障重构控制律，以保证飞行安全。

1 迎角余度配置及可靠性分析

1.1 余度配置

迎角传感器主要是向飞控控制律提供所需的飞机迎角反馈信号，一般安装在气流比较稳定的机头部位，具体安装位置一般由风洞试验确定。由于这一特殊要求以及空间限制，迎角传感器的机械余度很难按照电传飞行控制系统的基本四余度进行配置。例如，某型电传飞行控制系统飞机采用左风标式迎角传感器、右风标式迎角传感器及机头上下压差式迎角传感器，构成机械三余度配置，而每个机械余度具有电气两余度，如图1所示。

为了使多余度迎角信号有效协调的工作，需设计合理的余度管理策略，采取多通道信号选择、信号监控、信号隔离、故障后重构等措施。

图1 迎角传感器余度配置

1.2 可靠性分析

基于迎角传感器的这一特殊余度配置及余度管理策略，通过建立可靠性模型，进行可靠性计算分析。

而对于任务可靠性，同一风标或压差管的两个传感器之间为并联模型，且在全故障后采用了重构方式能保证安全，故三个机械余度的传感器信号为3表决1，其可靠性模型如图2所示。

图2 任务可靠性模型

而同样在全故障后采用了重构方式能保证安全，四余度配置的迎角传感器信号为4选1，其任务可靠性模型如图3所示。

图3 正常四余度配置的迎角传感器任务可靠性模型

按照可靠性模型，其涉及到串联模型、并联模型和表决模型，各类型模型的可靠性计算方法如下：

1）单个部件的可靠度：

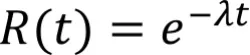
式中：R（t）—部件可靠度；

λ—部件失效率；

t—系统工作时间。

2）串联模型的可靠度：

式中：Ri(t)—部件可靠性；

Rs(t)—串联系统可靠性；

n—系统部件数。

3）并联模型的可靠度：

式中：Ri(t)—部件可靠性；

Rs(t)—并联系统可靠性；

n—系统部件数。

4）r/n（G）表决系统的可靠度

式中：Ri(t)—部件可靠度；

Rs(t)—r/n（G）系统可靠度；

n—系统部件数。

考虑到风标及压差管为机械部件，其可靠度可近似为1；为了便于计算，角位移传感器的可靠度和上下压差式传感器的可靠度同设为R0，两电气传感器的可靠度设为R1，三个机械余度的可靠度设为R2，标准四余度的可靠度设为R3，图2的可靠性计算如下:

根据图3可靠性框图，可靠度计算如下：

将R0作为f的函数，其函数关系如图4所示，从图中可以看出，在任一可靠度R0，其函数f均大于0，也就是 大于 ，即采用这一特殊迎角配置的可靠度大于传统四余度可靠度。

2 迎角故障后重构及影响分析

2.1 故障重构方法

迎角信号主要是保证飞机纵向静稳定性。多余度信号中个别通道故障时，对系统的稳定性、安全性影响不大，在极其严苛的情况下导致迎角信号全故障时，飞机纵向静安定性减弱，飞控系统迎角限制功能失效，可能影响到飞行安全。因此，为了提高电传飞行控制系统的可靠性和安全性，同时保证故障后飞机飞行品质及系统稳定性，需对迎角信号全故障后进行重构，重构方法如图5所示。

图4 R0与f的关系(横坐标为R0，纵坐标为f)

图5中SWAOAF表示控制律所采用的迎角反馈类型选择开关，SWAOAF=0，采用正常迎角反馈。SWAOAF=1，迎角传感器全故障，选择重构的迎角作为控制律反馈信号。重构的迎角由根据动静压计算出一理论的配平迎角和俯仰角速率解算的动态迎角相加得到，其计算公式如下：

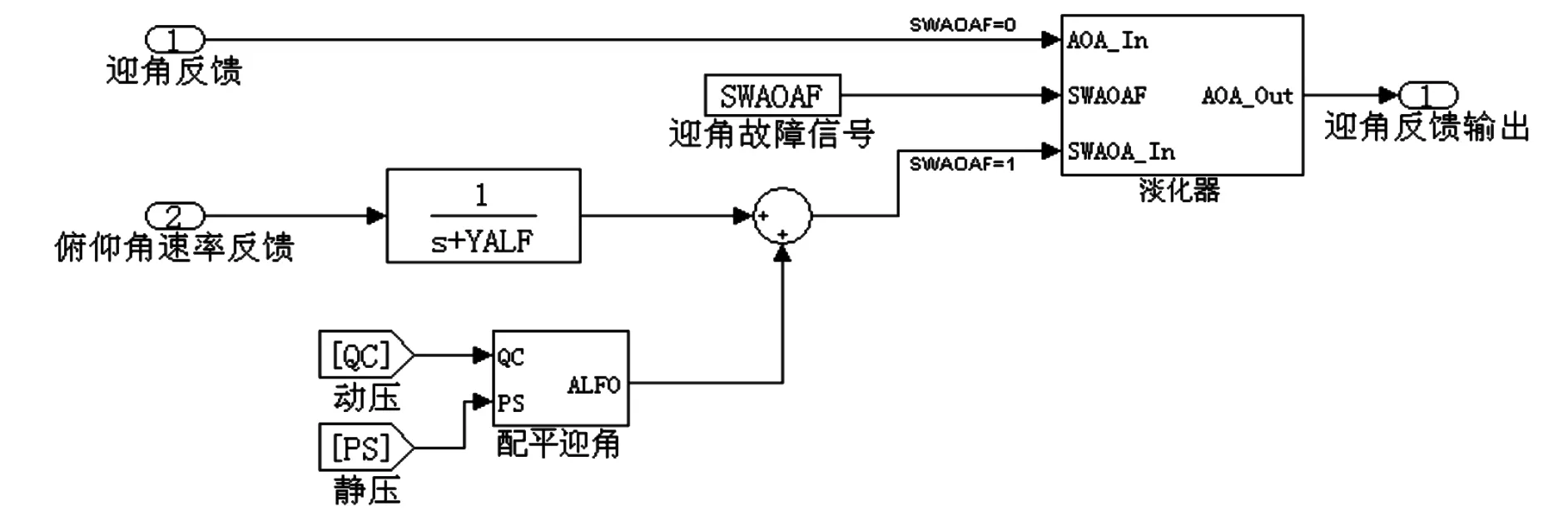
图5 迎角故障后控制律重构结构框图

其中：YALF参数根据动静压调参，体现了在不同飞行状态下俯仰角速率与迎角的动态换算关系。

上述公式第一项的配平迎角是对平飞状态进行静安定性补偿，保证飞机在平飞状态的飞行品质。第二项根据俯仰速率加惯性环节是对飞机机动特性进行补充反馈，保证飞机在机动过程中纵向静安定性，并保证飞机迎角不超过限制。

为保证迎角故障重构时转换瞬态较小，在转换为重构迎角的过程中采用淡化器来抑制瞬态，淡化器为下式的一阶惯性环节：

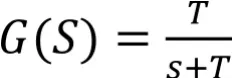
图6是正常迎角与重构迎角的纵向机动仿真对比，从图中可以看出，重构的迎角与真实迎角动态吻合性较好，且重构的迎角最大值为18.8°，小于迎角正常时的最大值25.8°，可以满足迎角故障后的安全飞行。

2.2 故障重构后的影响分析

通过仿真的手段来分析迎角故障重构后对系统的影响。主要从两个方面进行仿真验证，一是评估故障后对飞机瞬态的影响；二是评估故障后对飞行品质的影响。

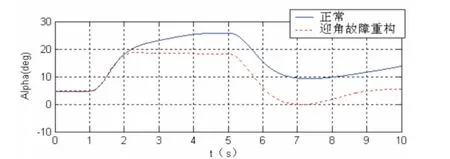
图6 正常迎角与重构迎角的对比

2.2.1 对飞机瞬态的影响分析

仿真过程中，采用六自由度非线性模型，基于某型飞机的气动力数据，选取典型状态点3km、0.4M进行分析。飞机进行纵向大机动飞行，在仿真时间第2s开始发生迎角传感器一次故障，第3s发生迎角传感器二次故障，第4s发生迎角传感器三次故障，如图7所示。

在迎角信号发生一次、两次故障时，飞行的过载变化小于0.1g，满足相关规范规定的0.5g的要求。在迎角信号发生最后一次故障时，飞机迎角减小2.3°，法向过载减小缓慢，在飞行员接受范围内，而后迎角减小至20°范围内，满足安全要求。

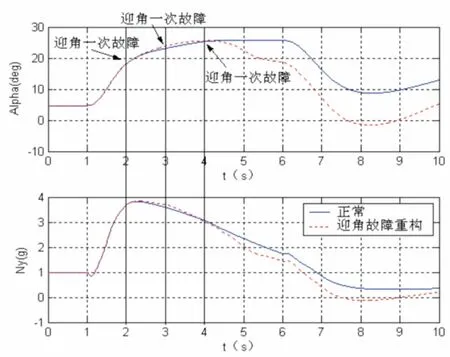
图7 纵向机动过程中迎角故障瞬态

2.2.2 对飞行品质的影响分析

考虑到迎角故障后主要影响飞机纵向飞行品质，对涉及到的纵向短周期频率、阻尼比、操纵期望参数、纵向稳定储备等参数进行评估。

首先，建立飞机纵向二自由度小扰动模型：

对小扰动方程进行拉氏变换，建立特征方程如下：

通常情况下，特征方程具有一对大的共轭复根及一对小的共轭复根（或两个小的实根），短周期模态特性主要受大的共轭复根影响，因此，可以根据大的共轭复根计算飞机的纵向模态特性。

飞机纵向特征方程一对大的共轭复根记为

则由此得短周期无阻尼振荡频率：

短周期阻尼比：

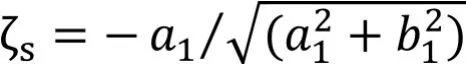
以0304（3km，0.4M）、0307、0805、0808状态点为例，对迎角正常和迎角全故障后的纵向短周期特性进行计算，其计算结果如表2所示。

迎角正常和迎角全故障后的纵向稳定储备计算结果如表3所示。

表1 短周期阻尼比标准

表2 纵向短周期特性对比

表3 纵向稳定储备对比

由表2和表3可以看出，在飞机配平状态，迎角故障情况下的飞行品质和稳定储备与迎角正常情况相比变化极小，满足相关规范的要求。

3 结 语

本文主要是针对三余度迎角传感器配置下可靠性进行分析，合理的余度管理策略可保证其可靠性满足可靠性设计要求。

同时，迎角信号全故障后，提出一种飞控系统控制律“伪迎角”重构方法，并通过构建小扰动模型及六自由度仿真模型进行仿真计算，该故障重构方法可保障迎角全故障后的飞机安全，其故障瞬态、飞行品质及系统稳定储备等满足相关规范要求。

[1]飞机设计手册.北京：航空工业出版社，2003.

[2]宋翔贵 张新国.电传飞行控制系统.北京:国防工业出版社,2001.