复合材料机械连接钉载分配有限元模拟方法研究

秦利军，杜 龙，吴早凤，熊 盼，黄晓霞

（中航工业洪都，江西 南昌 330024）

0 引 言

随着复合材料在现代飞机结构中应用比例的增加，复合材料连接和复合材料与金属间的混合连接等问题变得日益突出。复合材料连接主要包括胶接和机械连接两种。由于机械连接安全、可靠、可拆卸、传递载荷大和耐环境影响等突出优点，目前仍是工程结构中经常采用的一种连接形式[1,2]。

由于复合材料强度、刚度的各向异性和缺乏延性，在多钉机械连接中连接板上各孔的载荷重新分配能力差，各个连接孔上的承载比例相差大。通常情况下，连接件间由于材料、尺寸等参数的不对称会导致在多钉连接时各钉的载荷分配不均匀。在金属材料多钉连接中，承担大载荷的螺栓孔会先出现塑性区，使各钉载荷重新分配，各孔的承载趋于均匀；而在复合材料连接中，由于复合材料本身是一种脆性材料，不存在明显的塑性区，这样就使得在复合材料多钉连接时，各钉载荷不会随着总载荷的增加而重新分配，钉载分配呈现出严重不均匀性。复合材料连接钉载分配的不均匀性致使个别螺栓载荷比螺栓平均载荷高，如果再沿用金属均匀化强度校核方法计算复合材料连接件强度将比较危险。

确定复合材料层板多钉机械连接中每个螺栓的承载比例是计算多钉连接强度的基础，在工程设计与应用中一直受到高度重视。复合材料多钉连接的载荷分配计算主要有三种方法：试验方法、工程简化法和有限元法。随着有限元软件的成熟和计算机性能的提升，在多钉连接强度分析中，采用成熟的有限元方法确定多钉连接载荷分配得到了广泛的应用，并逐步成为了分析复合材料连接钉载分配的主要方法。实际工作中，常采用共节点法、MPC法、梁元法及弹簧元法等简化方法来确定钉载，但采用何种简化方法随意性较大，对简化模型的计算精度缺乏定量研究。采用接触算法模拟机械连接精度较高，但计算复杂度大，特别是多钉连接，往往会造成收敛困难。因此，有必要深入研究复合材料连接钉载分配的模拟方法，对比研究不同模拟方法的计算精度，以寻求满足工程计算精度要求且简单实用的有限元建模方法，可为解决实际工程问题提供参考。

本文基于有限元软件ABAQUS，首先研究了复合材料连接的不同模拟方法包括螺栓的简化方法和复合材料板的简化方法，并以一列三钉复合材料连接为例，建立了复合材料机械连接有限元模型；然后，结合试验结果对比分析了不同模拟方法下复合材料连接钉载分配的计算精度；最后，讨论了螺栓刚度对钉载分配的影响规律。

1 有限元方法

由于包含螺栓（铆钉）与孔、螺帽（墩头）与板以及板与板间的接触关系，复合材料连接是具有高度非线性的三维接触问题，接触区域的应力也颇为复杂，准确模拟复合材料连接真实应力状态难度较大。然而对于复合材料连接钉载分配问题，主要考察每个螺栓的承载大小及比例，通常不需要过于细致地刻画连接区域的应力应变状态，可以对复合材料连接进行简化处理，简化模型主要包括螺栓的简化和连接板的简化。

1.1 螺栓简化方法

1.1.1 传统简化方法

螺栓简化的传统方法主要包括节点绑定法 （包括共节点法和MPC法）、梁元法和弹簧元法等。节点绑定法可分为共节点法和多节点约束（MPC）法两种，该方法是螺栓最为常用也是最简单的简化方法，其基本思想是假设螺栓的刚度无限大，不考虑节点的相对变形，从而使被连接单元节点具有位移相等的变形协调关系。与节点绑定方法比，采用梁元可有效模拟螺栓的刚度，在不考虑接触应力和摩擦力的情况下，梁元是螺栓的较好近似。弹簧元法与梁元法类似，都可有效模拟螺栓的刚度，两者的主要区别是单元自由度不同。对于梁元，可通过一个单元实现螺栓六个自由度的刚度模拟，而弹簧元仅有一个自由度，在模拟螺栓拉伸刚度和剪切刚度时需建立多个弹簧元。

1.1.2 Fasteners单元法

在ABAQUS中提供了一种点对点的Fasteners连接方式，该方法最初主要用于焊接的模拟，在不关心孔周应力分布时，该方法也可用于螺栓、铆钉等机械连接。Fasteners单元采用独立网格技术，可以通过空间内任意一点沿给定方向向连接件投影创建Fasteners单元节点，并且Fasteners单元节点独立于有限模型网格节点，无需与网格节点一一对应[3]。Fasteners单元节点位移由定义的影响半径内有限元模型网格节点位移插值得到。通过对两节点间的连接单元赋予连接属性即可进行螺栓连接的模拟。选用Fasteners单元可以对大规模的钉群进行快速建模，而传统钉元两端点必须与有限元网格节点建立关联，在模拟时增加了工作量[4]。此外，Fasteners单元还可用于多层结构的连接，如图1所示。

图1 Fasteners连接方式示意图

Fasteners可搭配多种Connector section单元属性使用，如Beam和Bushing等。如图2所示，Bushing单元可以模拟连接点A、B间6个方向的刚度特性，本文主要考虑Bushing单元的拉压刚度和剪切刚度，螺栓承受拉压的刚度Kz为:

其中，E为螺栓材料的弹性模量，A为螺栓截面积，l为螺栓长度。螺栓承受面内剪切的刚度Kx和Ky可近似表示为：

其中，G为螺栓材料的剪切模量，A为螺栓截面积，l为螺栓等效长度。

图2 Bushing单元

1.2 复合材料板简化方法

1.2.1 复合材料壳元

如图3所示，在ABAQUS中可用两种壳单元模拟复合材料层合板，分别为常规的壳单元（二维壳单元）和基于连续体的壳单元（三维壳单元）。二维壳元通过定义单元的平面尺寸、表面法向和初始曲率，对参考面进行离散，但是常规壳单元不能定义壳的厚度，通过截面性质定义壳的厚度。基于连续体的壳单元类似于三维实体单元，可以对整个三维物体进行离散并建立数学描述，其本构行为采用了传统壳的本构模型。模拟接触问题，基于连续体的壳单元此常规的壳单元精确，因为它可以在双面接触中考虑厚度的变化。

在使用连续壳元模拟复合材料板时应注意以下几点：1）连续壳元可直接使用三维物体建立网格模型；2）与实体单元相同，节点只有三个自由度，分别为1，2，3；

3）连续壳元只能采用六面体和五面体单元；

4）根据单元节点排列顺序定义厚度方向，节点顺序的排列非常重要；

5）厚度方向每个单元都包含一个完整复合材料铺层，如果是两层以上，那么在每一层单元上都会赋予在Composite Layup中所有的铺层。

图3 常规壳元与连续壳元比较

1.2.2 实体单元

若不需要细致分析复合材料每个铺层的应力状态，可将复合材料层合板等效为各向异性均质材料处理，各向异性材料属性采用复合材料铺层的等效工程常数。采用这种材料等效的方法可减少铺层建模时间，更为重要的是可以采用三维实体单元建立复合材料板模型。采用三维有限元模型，可以完成厚度方向接触应力分析、预紧力分析以及间隙和干涉配合分析等二维模型无法实现的分析。

2 有限元模型

2.1 几何参数与材料参数

为便于与试验结果对比，复合材料连接采用文献[5]提供的几何参数和材料参数。图4为一列三钉的复合材料连接实例，两被连接板分别为复合材料层合板与铝板，几何参数为连接件板长195mm，宽30mm，孔径5mm，孔端距30mm，钉间距40mm，复合材料层板厚2.5mm，铝板厚8mm。复合材料为T300/648，铺层参数为[±45/02/90/02/±45/90]S，铝板材料为LY12，紧固件材料为30CrMnSiA，材料弹性常数如表1所列。

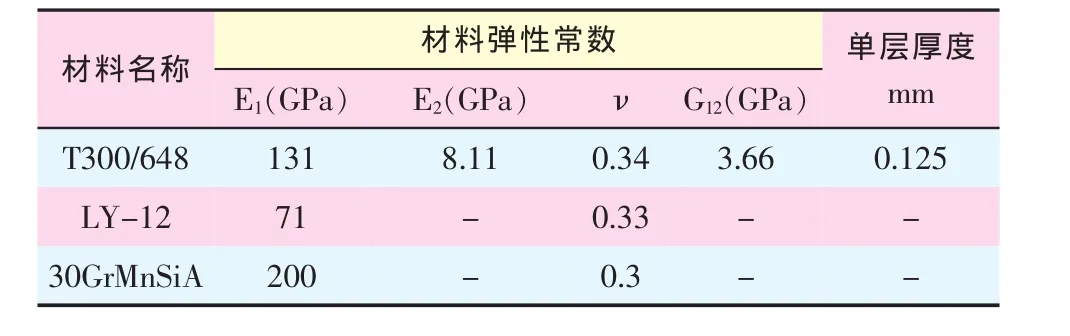
表1 材料弹性常数

2.2 基于节点绑定法的二维壳模型

当被连接点处于同一空间位置时可直接采用共节点的方法实现节点绑定，当被连接点存在一定间距时需要采用位移约束的方法实现节点绑定。在ABAQUS中，位移约束可通过MPC约束法或耦合约束法（Coupling）模拟，本文采用Coupling方法来约束（绑定）被连接点的自由度。模型的边界条件为左端固支，右端施加x方向载荷并约束其余5个自由度。图5为基于节点绑定法的二维壳模型。

图4 一列三钉连接件模型

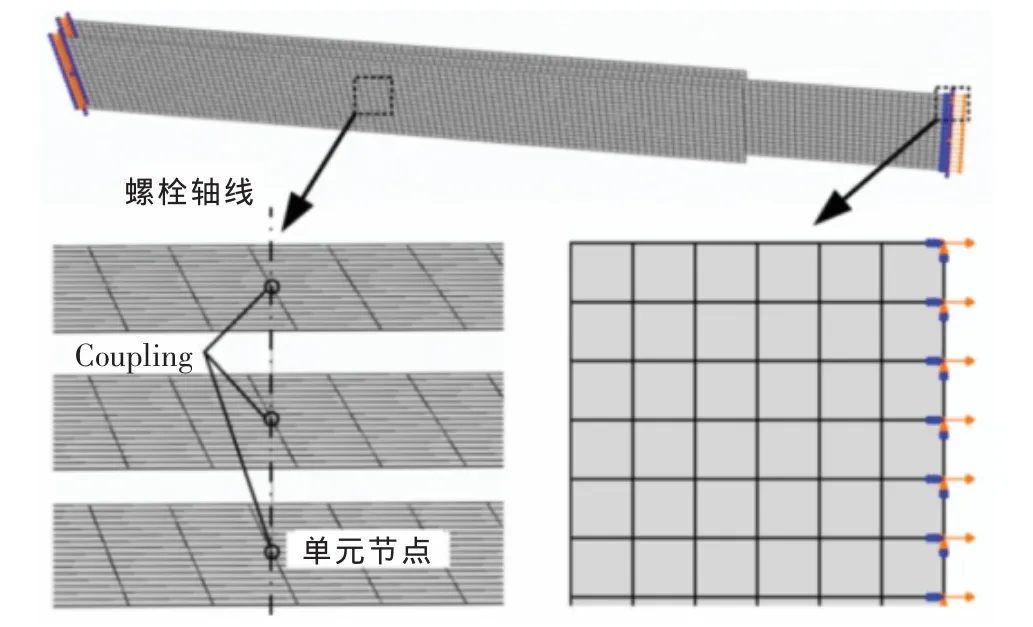
图5 基于节点绑定法的二维壳模型

2.3 基于梁元的二维壳模型

基于梁元的二维壳模型中，采用空间短粗梁单元B31模拟螺栓，梁单元截面选用圆形，截面半径取2.5mm，梁单元的剪切刚度由ABAQUS自动计算。梁单元节点与壳单元节点采用位移耦合的方法（Coupling）固结在一起。图6为基于梁元的二维壳模型。

2.4 基于弹簧元的二维壳模型

基于弹簧元的二维壳模型中，采用二节点弹簧单元Spring2模拟螺栓，弹簧刚度计算方法参见1.1.2节。图7为基于弹簧元的二维壳模型。

2.5 基于Fasteners连接的二维壳模型

图6 基于梁元的二维壳模型

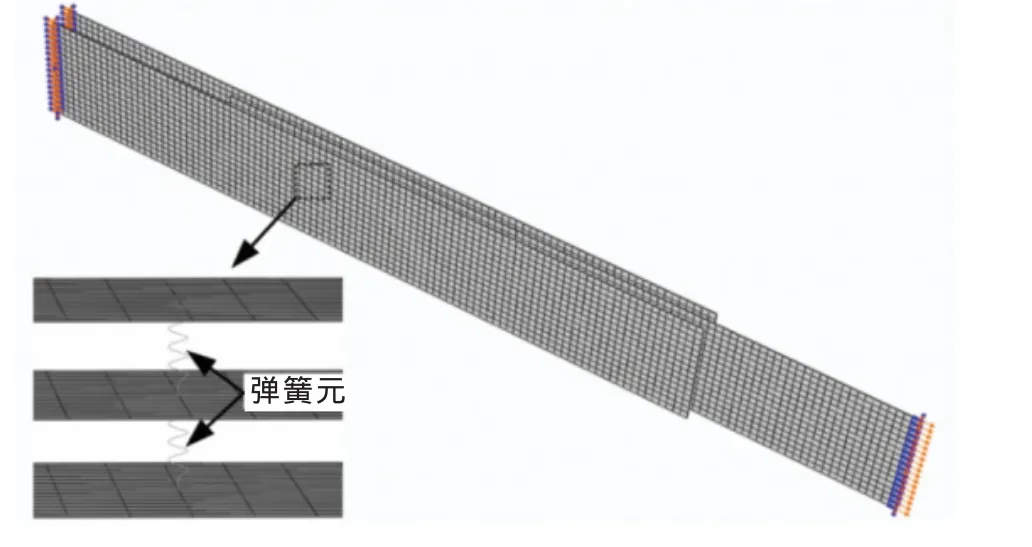
图7 基于弹簧元的二维壳模型

采用Fasteners连接方式建立复合材料连接模型时，首先是在螺栓轴线上设定参考点（对于多排多列连接可通过阵列的方式快速建立参考点）；然后定义Fasteners连接的连接属性（Connector section）；最后通过引用建立好的参考点和连接属性便可以实现螺栓的Fasteners连接。如图8所示，ABAQUS中提供了多种连接属性可供用户使用，对于机械连接可采用Beam和Bushing连接属性来模拟螺栓，其中Beam连接属性表示连接为刚性连接，同时约束被连接点的6个自由度，而Bushing连接属性可以通过用户定义的方式设置连接刚度。图9为创建Fasteners连接的编辑窗口，通过Connector section下拉菜单选择已建立好的连接属性，通过影响域半径（Influence radius）模拟螺栓的尺寸。图10为基于Fasteners连接的二维壳模型。

2.6 基于接触方法的三维模型

如图11所示，采用三维接触模型建立连接件的三维模型。考虑到对称性，建立一半模型并施加对称边界条件。模型中，螺帽与螺栓间建立位移耦合条件（tie），其它接触面采用弹性体对弹性体的接触对，接触算法为硬接触算法。模型中未考虑摩擦力对连接件力学性能的影响。铝板和螺栓采用六面体实体单元C38I，复合材料板分别采用三维壳元SC8R和正交各向异性体元C38I。

图8 Connector连接属性

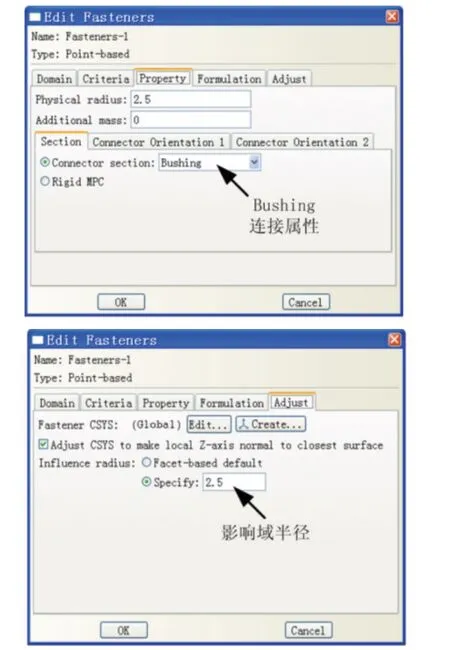
图9 创建Fasteners连接

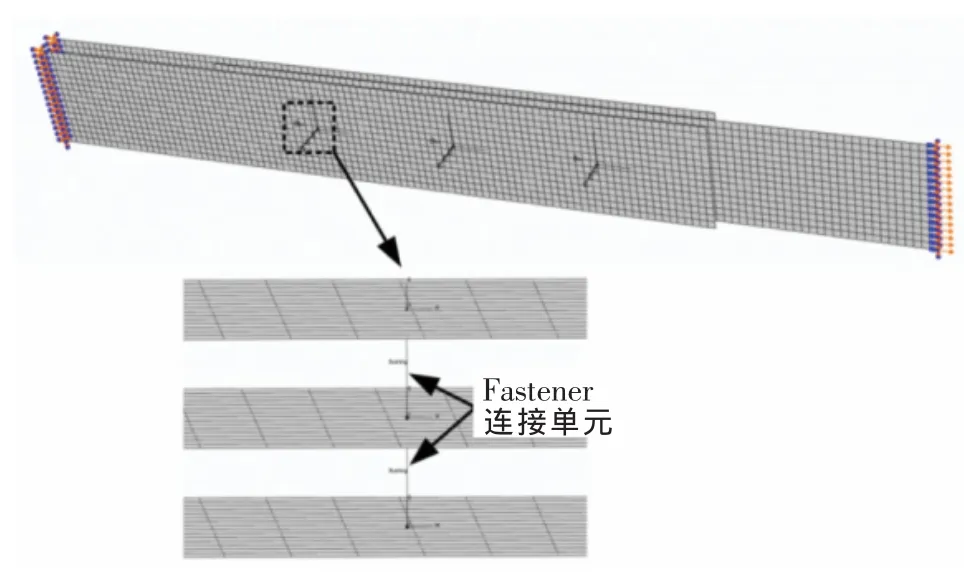
图10 基于Fasteners连接的二维壳模型

图11 基于接触方法的三维模型

3 计算结果

3.1 螺栓简化方法计算结果

表2为螺栓不同简化模型下计算结果与试验结果的比较。通过试验结果可以看出，一列三钉复合材料连接在外载下各钉传递的载荷分别为总载荷的27%，24.3%和49.1%，钉载分配具有严重不均匀性，最大钉载与最小钉载相差约25%，可见多钉连接中，各钉传递的载荷差异很大，这大大降低了多钉连接的连接效率。

对比计算结果与试验结果，可以看出除Beam属性的Fasteners连接模拟方法外，有限元计算结果与试验结果吻合性较好，二者最大偏差为6.3%。从螺栓简化模型角度看，不同模拟方法的计算结果存在一定差异，其中Beam属性Fasteners连接模拟方法误差最大，偏差为15.7%，而节点绑定法、梁元法、弹簧元法和Bushing属性的Fasteners连接法差异不大，这三种简化方法均可较为精确模拟复合材料连接的钉载分配。从表2还可以看出，三维接触方法用于复合材料连接的钉载分配问题时，相较螺栓简化模型没有明显优势，在处理主要关心钉载分布的工程问题时，采用螺栓简化模型可满足工程精度要求。

表2 计算结果与试验结果对比

3.2 复合材料板简化模型计算结果

图12为二维复合材料板模型下的钉载分配计算结果，可以看出采用复合材料铺层方式下的二维壳元和采用等效各向异性下二维壳元模型所得结果非常接近，对于三维壳元和实体单元也类似的结论（如图13所示）。也就是说，对于复合材料连接钉载分配问题，用等效各向异性材料属性进行建模分析便可得到较高计算精度。由于等效各向异性材料参数仅与复合材料铺层比例相关，与铺层次序无关，图12和图13也可解释为复合材料的面内刚度对钉载分配比例的贡献较大，而厚度方向的刚度分布对钉载分配的影响不明显。

图12 二维复合材料板模型下钉载分配

图13 三维复合材料板模型下钉载分配

4 分析与讨论

由前面的计算结果不难发现，复合材料连接的钉载分配主要受两连接板的面内拉伸刚度比和各螺栓间的剪切刚度比的影响，而板模型的维度（二维或三维）和螺栓的简化方式对复合材料连接的钉载分配的影响不显著。对于螺栓的简化，应保证简化模型可以体现出螺栓间的刚度比例。如图14所示，若改变受载最大的第3个铆钉的刚度（其余2个铆钉仍采用钢钉），将其改为钛铆钉和铝铆钉后，各钉承载比例发生明显变化。从图中可以看出，随着第3个铆钉的刚度的降低，其钉载比例相应下降，钉载的不均匀分布有所改善。

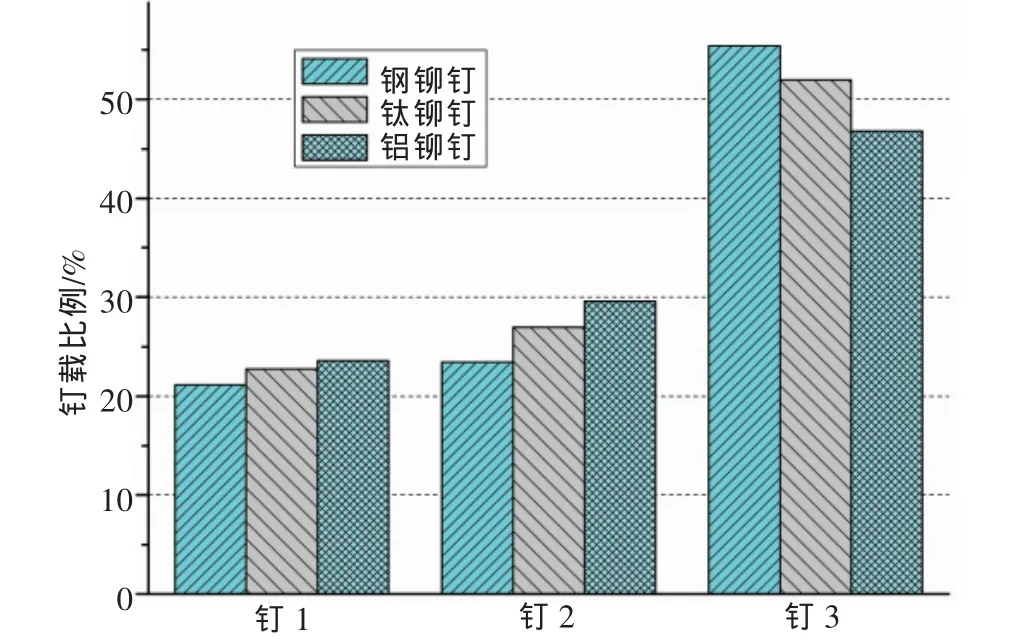
图14 不同铆钉下的钉载分配

5 结 论

复合材料连接的传力特性是复合材料结构设计的基础，研究其钉载传递特性和分配关系具有重要工程价值。本文基于有限元软件ABAQUS，以一列三钉复合材料连接为例，系统研究了复合材料连接的不同模拟方法，对比分析了不同模拟方法下复合材料连接钉载分配的计算精度，并得出以下结论：

1）解决复合材料连接的钉载分配问题时，三维接触方法相较简化模型没有明显优势，采用二维壳元和螺栓简化模型可满足工程精度要求。

2）复合材料连接钉载分配仅与被连接板的面内刚度相关，可采用等效各向异性材料属性模拟复合材料层合板。

3）对于螺栓刚度相同的多钉连接载荷分配计算，节点绑定法、梁元法、弹簧元法和基于Bushing属性的Fasteners连接方法差异不大，均可获得与三维接触方法相当的计算精度；对于螺栓刚度不同的情况，应采用能反应螺栓刚度的梁元法、弹簧元法和基于Bushing属性的Fasteners连接方法。

[1]谢鸣九.复合材料连接[M].上海：上海交通大学出版社，2011.

[2]赵美英，阎国良，顾亦磊，等.复合材料层板钉群连接载荷分配计算方法研究[J].航空计算技术，2006，36(3):97-101.

[3]Abaqus 6.10 documentation.

[4]钱一彬，钟小丹，陈普会，等.复合材料机身壁板的纵向连接设计与失效分析[J].航空学报，2012,33 (8):1427-1433.

[5]顾亦磊.复合材料机械连接强度分析及影响因素研究[D].西安：西北工业大学，2006.