某型教练机框梁结构分析及尺寸优化

张 勇，周 恒，余志明，陈里根，林振华

(中航工业洪都,江西 南昌330024)

0 引 言

在仿真技术成熟的今天，CAE技术的飞速发展，为产品生产前进行性能评估、提高产品品质、低成本设计提供了一个非常有效的工具。CAE不仅能起到性能分析的作用，还可通过先进的优化设计方法，实现结构的优化设计及减重，从而达到仿真驱动设计的目的。使用优化分析的方法，通过设定一系列优化参数，提交优化软件计算得出满足条件的结构参数，然后验证分析，能够大大提高设计效率，并且在保证性能的同时实现优化设计的目的。

某型飞机框梁位于1框和3框之间，并通过4只螺栓进行连接，对结构起支撑作用，如图1所示。某工况下在梁中心处承受大小为5661.8N的集中力，其材料为LY12，力学参数为：弹性模量E=71GPa，泊松比μ=0.33，密度ρ=2800kg/m3，强度极限σb=390 MPa。为了保证梁满足飞机结构设计中的强度要求，需要对其进行强度校核，本文应用有限元法和工程梁方法对梁进行强度分析，针对其强度不满足要求的问题，采用工程上常用的尺寸优化方法对梁进行改进设计，将梁截面尺寸作为优化设计变量，在一定强度和刚度外界约束条件下尽量使梁的体积最小化。

图1 梁CAD模型

1 尺寸优化数学模型

1.1 结构优化的数学模型

优化设计有三要素，即设计变量、目标函数和约束条件。设计变量是在优化过程中发生改变从而提高性能的一组参数；目标函数就是要求的最优设计性能，是关于设计变量的函数；约束条件是对设计的限制，是对设计变量和其他性能的要求。

优化设计的数学模型可以表述为：

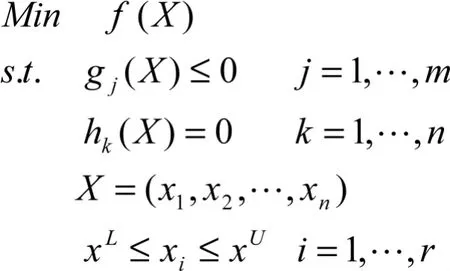
式中：X是设计变量；f(X)是目标函数；g(X)是不等式约束函数；h(X)是等式约束函数 上标U、L分别指上、下限。

目标函数f(X)；约束函数g(X)、h(X)是从有限元分析中获得的结构响应。设计变量X是一个矢量，它的选择依赖于优化类型。在拓扑优化中，设计变量为单元的密度；在尺寸优化（包括自由尺寸优化）中，设计变量为结构单元的属性；在形貌优化和形状优化（包括自由形状优化）中，设计变量为形状扰动的线性组合因子[1]。

1.2 尺寸优化

在保持结构的形状和拓扑结构不变的情况下，寻求结构组件的最佳截面尺寸以及最佳材料性能的组合关系，优化截面的最优面积（如图2桁架），选择板的最佳厚度等称为尺寸优化，其特点是：设计变量容易表达，求解理论和方法成熟[2]。

图2 尺寸优化示意

尺寸优化是一种细节优化设计方法，是设计人员在概念设计的基础上所进行的设计。它是通过改变结构单元的属性——例如壳单元厚度、梁单元的横截面属性、弹簧单元的刚度和质量单元的质量等，以达到一定的设计要求（如应力、质量、位移等），其优化流程如图3所示。

2 梁有限元分析

将梁抽取中面，简化为二维单元进行面网格划分，其中，加强筋用三角形单元划分，其余用四边形单元划分，得到11576个节点、10536个四边形单元、1443个三角形单元。由于梁是用螺栓连接于1框和3框，所以在两端四个螺栓孔处建立四个rbe2刚性单元，用于外界约束，约束X、Y、Z三个方向上的平动自由度，并在梁底面中心处施加正Y向大小为5661.8N的集中力，其有限元模型如图4所示。

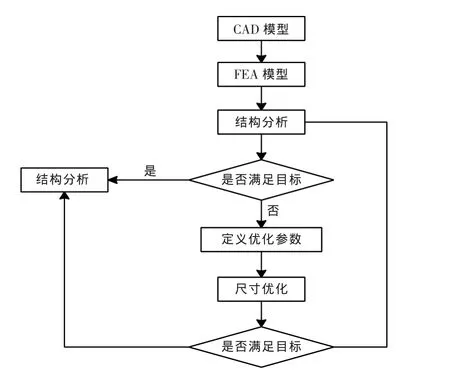
图3 尺寸优化流程

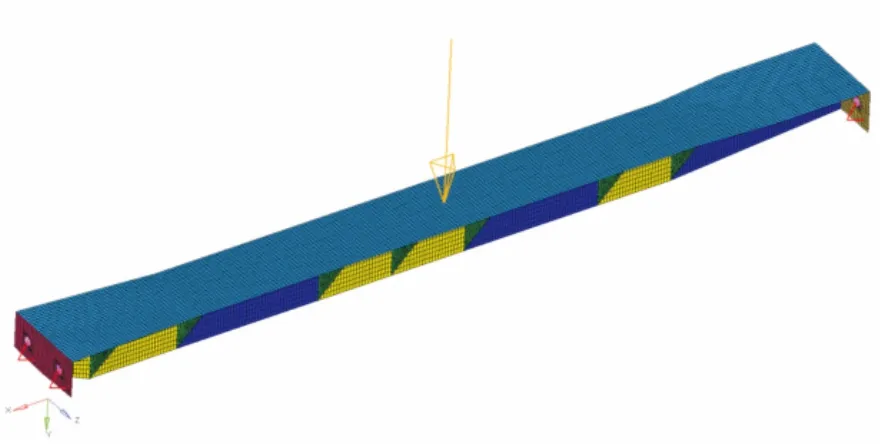
图4 梁有限元模型

赋予梁相应厚度属性后，将有限元模型提交有限元分析软件计算，得到梁变形和应力结果如图5、图6所示。

图5 梁变形

图6 梁应力图

由分析结果可知，在受力处产生最大变形，大小为4.7mm，在最小截面处端部产生最大应力，大小为497.85Mpa，大于材料LY12的强度极限390Mpa，所以，梁强度不够。

3 梁工程梁分析

为了进一步验证梁强度是否足够，用工程算法对梁进行强度校核。工程上，为便于分析计算，考虑其弯曲变形，将梁简化成简支梁来处理，其中截面AA和B-B是危险截面，其截面形式及受力情况简图如图7所示。

图7 梁截面形式及受力简图

对A-A截面：

形心C1的纵坐标：

A-A截面对形心轴Zc1的惯性矩：

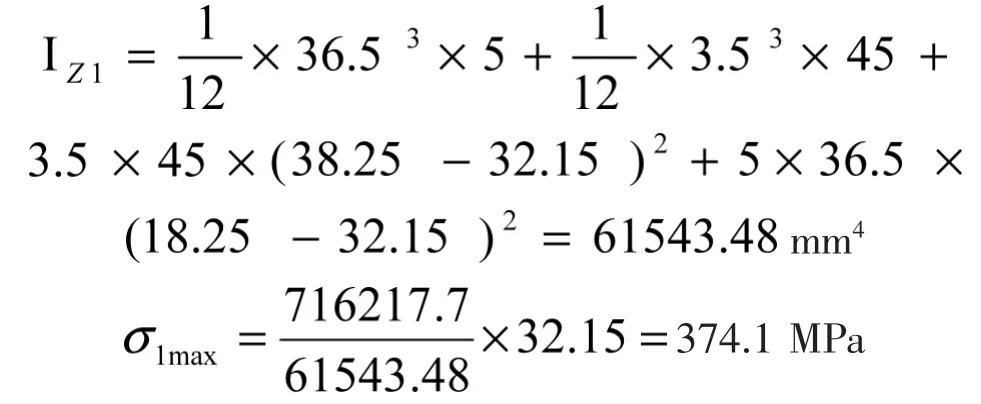
其结果如图8所示。

对B-B截面：

形心C2的纵坐标：

图8 A-A截面应力

B-B截面对形心轴Zc2的惯性矩：

其结果如图9所示。

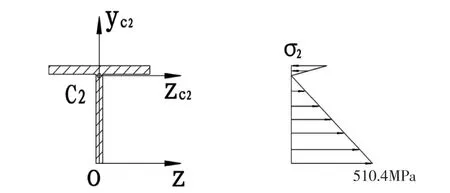
图9 B-B截面应力

由上述工程分析结果可知，在危险截面B-B处端部，最大应力为510.4Mpa，大于材料LY12的强度极限390Mpa，故梁强度不够。

综上，梁有限元分析和工程分析结果相差2.46%，而最大应力结果都大于使用材料的强度极限，所以梁强度不够。因此，采用工程上常用的方法对梁进行尺寸优化，在一定强度和刚度约束条件下应尽量使梁的体积最小化。

4 梁尺寸优化

给定材料密度，在满足强度和刚度条件下，对梁进行尺寸优化，使体积最小化。其数学优化模型如下所示：

式中：K是结构总体刚度矩阵；U是节点位移；F是外力；d是力作用点处位移；V是梁的体积；X是设计变量，其中x1是梁加强筋厚度； x2是非加强筋处梁腹板厚度；x3是梁底板厚度；x4是加强筋处梁腹板厚度。

将添加了设计变量、外界约束、目标函数的梁有限元模型提交OptiStruct运算，经过4次迭代，设计变量、外界约束、目标函数趋于收敛，其迭代图如图10~图15所示。

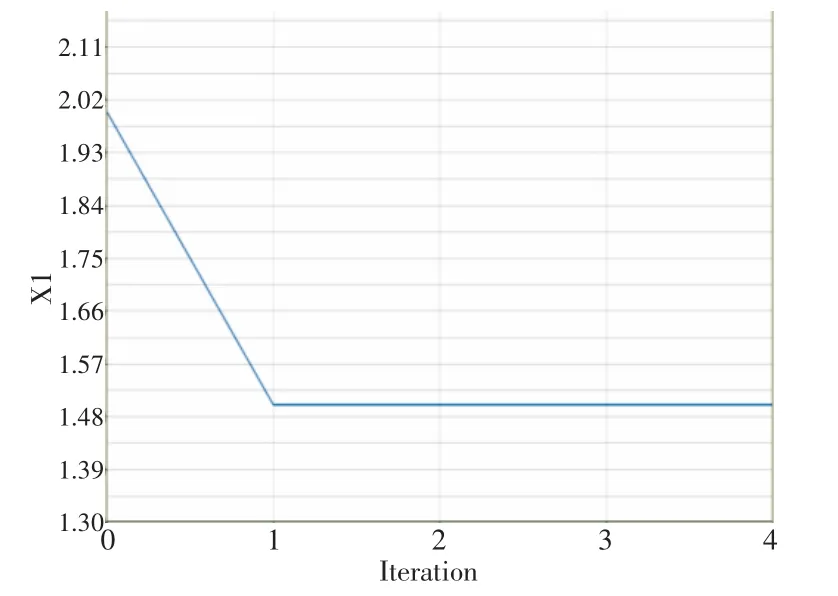
图10 设计变量X1迭代图

图11 设计变量X2迭代图

图12 设计变量X3迭代图

图13 设计变量X4迭代图

图14 力作用点变形迭代图

图15 体积迭代图

优化前后，各设计变量、外界约束、目标函数对比如表1所示。

表1 优化前后对比

经过优化，梁最大变形为 3.82mm，减小了18.7%，最大应力为319.8MPa，降低了35.8%，在满足强度和刚度约束条件下，梁的体积为200360mm3，增加了14.9%。优化后，梁的应力水平小于材料的强度极限，剩余强度系数为1.22，满足了强度要求。

5 结语

通过对某型飞机梁的结构分析和尺寸优化，可以得到以下结论：

1）在某工况下对梁进行强度校核，经过有限元分析和工程梁分析，梁强度不够，需对梁进行重新设计。

2）采用工程上常用的方法对梁进行尺寸优化设计，获得梁各部位尺寸优化结果，得到梁的优化形式，在满足一定强度和刚度约束条件下使梁的体积最小化。

3）结构的优化结果一般偏理想化，实际情况中可以作为设计参考的依据对结构进行改进设计，在满足外界约束条件下达到实际应用的目的。

[1]张胜兰,郑冬黎等.基于HyperWorks的结构优化设计技术[M].北京:北京工业出版社,2007.

[2]左孔天.连续体结构拓扑优化理论和应用研究[D].武汉：华中科技大学,2004,9.