复合材料墙腹板开孔补强稳定性分析

李朝光，杜 龙，姜亚娟，徐 丹，孙 敏

（中航工业洪都，江西 南昌330024）

0 引 言

根据设计要求，常常需要在飞机结构上开孔。开孔不仅会因切断了纤维引起复合材料构件整体刚度和强度的下降，而且还会改变结构的失稳破坏模式。因此，复合材料构件开孔部位一般要进行补强设计。对此，国内外进行了大量的理论和试验研究，寇长河等对大开孔复合材料层合板不同补强形式进行了研究，发现插层补强优于面外补强，对称补强优于非对称补强[1,2]。O'Neil针对非对称补强问题进行了研究[3]，发现补强后板的强度提高了5%～12%。Pickett针对顺序铺层对称补强问题进行了研究[4]，发现补强后板的强度提高了29%～40%。他们的研究均表明，非对称补强之所以效率较低，主要是由于补强区域的附加弯矩引起了较高的层间应力，从而降低了复合材料构件的承载能力。

复合材料墙一般是飞机的重要受力构件，在墙腹板上开有工艺通孔或过油孔，在剪切载荷作用下，墙腹板最主要的失效模式为屈曲失效，为保证整个结构具有较高的承载能力，必须对复合材料墙腹板进行开孔补强稳定性分析。本文采用MSC.Patran/ Nastran有限元分析软件对剪切载荷作用下复合材料墙腹板开孔对称补强稳定性问题进行了分析，并与相同条件下复合材料墙腹板在无孔和开孔时的稳定性作了对比研究。

1 无孔复合材料墙腹板稳定性分析

复合材料墙腹板典型几何模型如图1所示，材料采用HF10A/NY9200GA，尺寸大小取为200mm× 150mm×4mm，铺层为[±45/0/±45/±45/90]2s。采用Patran软件建立了复合材料墙腹板典型单元的有限元模型，运用Nastran软件进行线性屈曲分析。划分网格时采用QUAD4单元，QUAD4单元的每个节点有6个自由度，分别为：Ux、Uy、Uz、Rx、Ry和Rz。

计算模型边界条件取为四边简支：

两长边：Uy=Uz=0，Ry=Rz=0。

两短边：Ux=Uz=0，Rx=Rz=0。

加载方式为：在墙腹板周边施加剪切载荷，根据剪应力互等定理和墙腹板的几何参数，在墙腹板长边施加120KN的载荷，在墙腹板短边施加90KN的载荷。

采用Patran软件的Buckling分析模块对该复合材料墙腹板进行稳定性分析，通过计算可得其一阶屈曲特征值为2.4735，说明墙腹板在上述载荷下未发生屈曲。

图1 复合材料墙腹板典型几何模型

2 开孔复合材料墙腹板稳定性分析

在复合材料墙腹板上开孔，研究开孔对其稳定性的影响。本文选取圆形开孔方式，其几何模型如图2所示，其中：H为开孔圆心到墙腹板上边缘的距离，h为开孔圆心到墙腹板下边缘的距离；w为复合材料墙腹板的宽度；d为开孔孔径。采用Patran软件建立了复合材料墙腹板典型单元的有限元模型，运用Nastran软件进行线性屈曲分析，有限元模型如图3所示，一阶屈曲模态图如图4所示。

图5给出了在不同d/w情况下一阶屈曲特征值随H/h的变化曲线，图6给出了在不同H/h情况下一阶屈曲特征值随d/w的变化曲线。

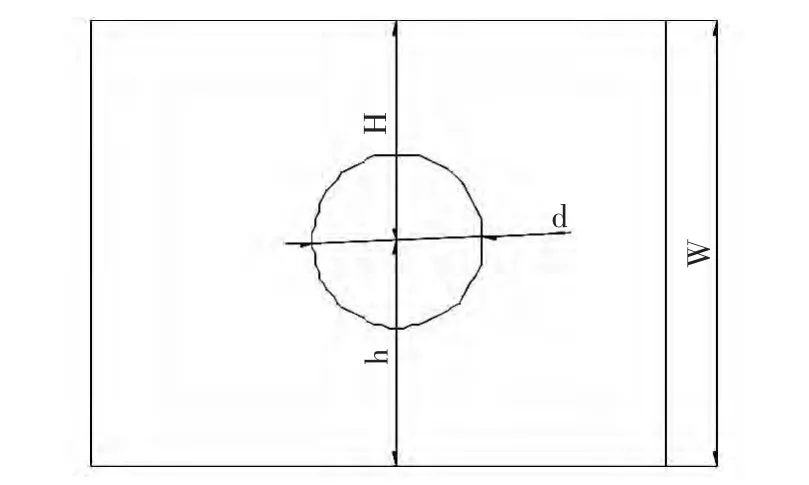
图2 开孔复合材料墙腹板几何模型

图3 开孔复合材料墙腹板有限元模型

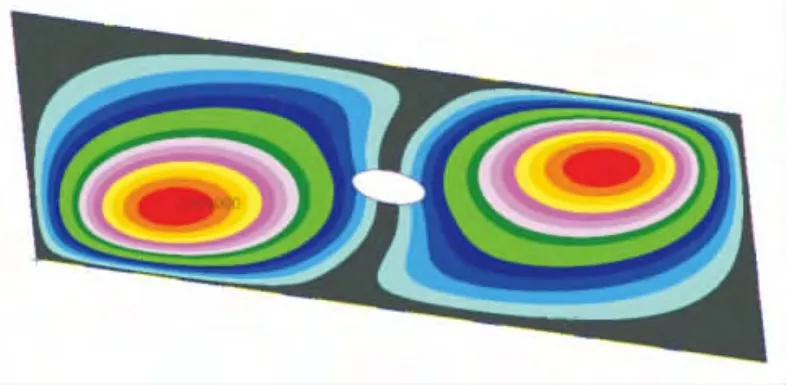
图4 开孔复合材料墙腹板一阶屈曲模态图

图5 一阶屈曲特征值随H/h的变化曲线

从图5中可以看到，在不同d/w情况下，一阶屈曲特征值随H/h的变化曲线明显不同。在d/w较小的情况下，随着H/h值的增大，一阶屈曲特征值也随之增大，如d/w=0.13时，H/h=1.0和H/h=2.0的一阶屈曲特征值分别为2.3709和2.3939，另外，在d/w较小的情况下，随着d/w值的增大，一阶屈曲特征值随H/ h的变化曲线逐渐变陡，但d/w值增大到一定程度，一阶屈曲特征值随H/h的变化曲线逐渐由陡变缓，如d/w=0.33时一阶屈曲特征值随H/h的变化曲线明显比d/w=0.27时一阶屈曲特征值随H/h的变化曲线平缓。在d/w较大的情况下，随着H/h值的增大，一阶屈曲特征值又随之变小，如d/w=0.33时，H/h=1.0和H/h=2.0的一阶屈曲特征值分别为1.7852和1.7465。

从图6中可以看到，在不同H/h情况下，临界载荷随d/w的变化曲线基本一致。在H/h较小的情况下，临界载荷随d/w的变化曲线基本重合，随着H/h值的变大，曲线逐渐变陡，临界载荷趋于变小。

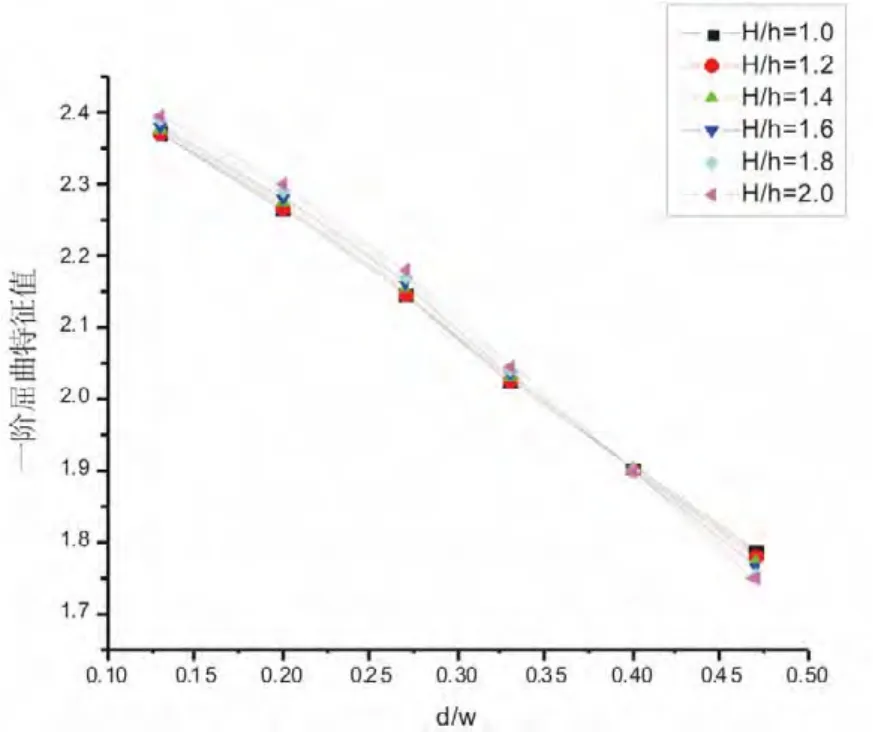
图6 一阶屈曲特征值随d/w的变化曲线

3 开孔补强复合材料墙腹板稳定性分析

采用顺序铺设的对称补强方法对墙腹板开孔周围的环形区域进行均匀对称补强。补强区的几何参数如图7所示，其中：D为补强区直径；d为开孔孔径；t为复合材料墙腹板厚度；T为补强区厚度，不同的补强区厚度比T/t对应的铺层参数见表1。

1）不同开孔孔径下补强宽度比对稳定性的影响

图8给出了开孔位于墙腹板中央位置时不同d/ w情况下一阶屈曲特征值随D/d的变化曲线，同时给出了未开孔板的一阶屈曲特征值，其中，D/d=1表示未增强板。

从图8中可以看出，补强提高了复合材料墙腹板的稳定性。未补强时，一阶屈曲特征值随着孔径的增大而减小；补强后随着d/w的增大曲线变陡，说明补强宽度比D/d对大开孔墙腹板的稳定性影响较大，对小开孔墙腹板的稳定性影响较小。如d/w为0.2且开孔情况下，D/d为2.0时临界荷载只比D/d为1.25提高了4.06%；而d/w为0.47时，D/d为2.0时临界荷载比D/d为1.25时提高了17.17%。所以当孔径较小时，可以根据实际情况决定是否补强，即使补强也可以选择较小的补强宽度比，从而在增重较小的情况下取得较好的补强效果；而当孔径较大时，需选取较大的补强宽度比，从而可以获得较好的补强效果。

图7 补强区几何参数示意

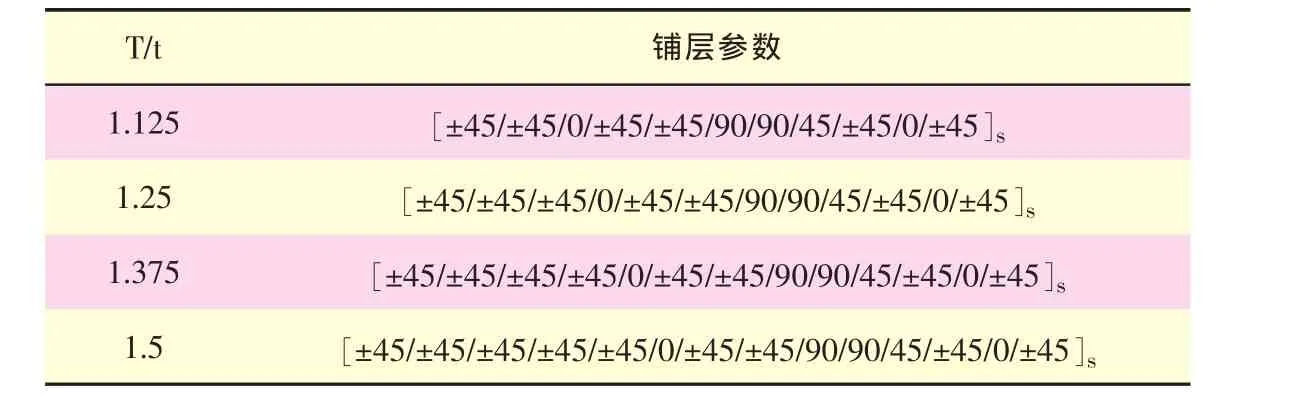
表1 不同的补强区厚度对应的铺层参数

2)不同开孔孔径下补强厚度比对稳定性的影响

图9给出了开孔位于墙腹板中央位置且补强宽度比D/d为1.5时，不同d/w情况下，一阶屈曲特征值随T/t的变化曲线，同时给出了未开孔板的一阶屈曲特征值，其中，T/t=1表示未增强板。

从图9中可以看出，随着补强厚度比的提高，不同d/w情况下的一阶屈曲特征值都有所增加。补强后随着d/w的增大曲线变陡，说明补强厚度比T/t对大开孔墙腹板的稳定性影响较大，对小开孔墙腹板的稳定性影响较小。如d/w为0.2且开孔情况下，T/t为1.5时临界荷载只比T/t为1.125时提高了5.9%；而d/w为0.47时，T/t为1.5时临界荷载比T/t为1.125时提高了22.55%。所以，当孔径较小时，可以根据实际情况决定是否补强，即使补强也可以选择较小的补强厚度比，从而在增重较小的情况下取得较好的补强效果；而当孔径较大时，需选取较大的补强厚度比，从而可以获得较好的补强效果。

图8 一阶屈曲特征值随D/d的变化曲线

图9 一阶屈曲特征值随T/t的变化曲线

4 结 论

1）开孔孔径的大小对复合材料墙腹板的稳定性影响较大，随着孔径的增大，复合材料墙腹板的一阶屈曲特征值近似呈直线降低。但是当开孔孔径较小，且位于板中央时，对稳定性的影响较小。

2）开孔位置对复合材料墙腹板的稳定性有一定影响。孔径较小情况下，开孔位置偏离墙腹板的中央位置时，复合材料墙腹板的稳定性略有提高；孔径较大情况下，开孔位置偏离墙腹板的中央位置时，复合材料墙腹板的稳定性略有降低。

3）补强提高了复合材料墙腹板的稳定性。随着补强宽度比和补强厚度比的增大，复合材料墙腹板的稳定性逐渐提高。

4）随着孔径比的增大，补强宽度比和补强厚度比对复合材料墙腹板稳定性的影响增大。

[1]寇长河，汪彤，郦正能，等.复合材料层合板开孔补强研究[J].北京航空航天大学学报，1997，23：477-481.

[2]杨乃宾，章怡宁.复合材料飞机结构设计[M].北京：航空工业出版社，2002.

[3]O'Neill G S.Asymmetric reinforcements of a quasi-isotropic graphite epoxy plate containing a circular hole [D].Monterey,California,USA：Naval Postgraduate School,1982.

[4]Pickett D H,Sullivan P.Analysis of symmetric reinforcement of quasi-Isotropic graphite-epoxy plates with a circular cutout under uniaxial tensile loading[D]. Monterey,California,USA：Naval Postgraduate School, 1983.