中国通货膨胀持续性的非对称特征研究——基于分位数自回归模型和分位数单位根的研究

彭小静，邓 明，吴 亮

(1.江南大学商学院，江苏 无锡 214122;2.厦门大学经济学院，福建 厦门 361005;3.阜阳师范学院经济学院，安徽 阜阳 236041)

一、引言与文献综述

稳定物价是各国货币政策的最重要的目标之一，将通货膨胀维持在合理范围也一直是各国货币当局的核心工作之一，我国政府同样一直将调控通货膨胀作为政府工作的重点之一。鉴于通货膨胀对于政府宏观调控和短期经济波动有着重要意义，各国学者也对通货膨胀的理论做了大量研究。关于通货膨胀的动态特征尤其是通货膨胀持续性的研究尤为引人关注。Fuhrer和Moore(1995)指出通货膨胀持续性(也称为通货膨胀惯性)是指在对通货膨胀率施加随机冲击后，其回复到长期均衡水平上持续的时间［1］。当具有高通胀持续性时，价格在受到冲击偏离长期均衡后回到初始水平所需要的时间较长，从而对实体经济造成冲击会持续更长的时间，加大货币当局调控通货膨胀的难度，降低通货膨胀的成本也越高。由此可见，通货膨胀持续期的长度会对以稳定物价为主要目标的货币政策产生较大影响，货币当局唯有准确把握本国或本地区通货膨胀的动态性质，才能更加有效地选择货币政策实施的时机与力度。

由于建立在理性预期基础上的早期的新凯恩斯模型不能描述现实经济中的通货膨胀持续性特征，研究者们为了解释通货膨胀持续性特征，从不同视角对新凯恩斯模型进行扩展。Phelps(1978)和Taylor(1980)利用叠交工资契约模型从理论上推导出通货膨胀具有持续性［2］［3］。Roberts(1998)在研究中提出了不完全理性预期假说。该假说认为人在通货膨胀预期的形成这一问题上可以分为非理性的和完全理性的两类。非理性者在预测未来的通货膨胀时仅利用适应性预期，导致通货膨胀持续性高［4］。Mankiw和Reis(2002)通过构建粘性信息模型来阐述通货膨胀持续性，并用数值模拟得到了较为符合美国实际情况的通货膨胀持续性特征［5］。此外，许多研究文献对通货膨胀的持续性展开了实证研究，例如，Taylor(2000)、Stock(2001)、Pivetta和Reis(2007)、Kumar和Okimoto(2007)等文献对美国的通货膨胀持续性进行了实证研究［6］［7］［8］［9］;Lee和Wu(2001)、Levin和Piger(2004)、Cuestas和Harrison(2010)对OECD和欧元区的通货膨胀持续性进行了研究［10］［11］［12］。

总体而言，对于通货膨胀惯性是否存在，研究者得出的结论基本一致。在此基础上，研究者将更多注意力放到通货膨胀惯性是否因货币政策的不同而变化这一问题上，但这方面的研究目前未有一致结论。Taylor(2000)利用中位数无偏估计方法对美国通货膨胀的研究表明，美国通货膨胀持续性在1982年之后有下降的趋势［6］;Stock(2001)发现美国通货膨胀持续性没有发生改变［7］;而Pivetta和Reis(2007)使用贝叶斯估计方法、滚动视窗方法以及中位数无偏估计方法等多种方法对美国的通货膨胀率进行估计，发现美国的通货膨胀率持续性在过去的三十年里没有变化［8］;Gagea和Mayoral(2006)利用分数次积分方法研究了21个OECD国家的通货膨胀惯性，发现OECD国家过去四十年来的通货膨胀惯性并未改变［13］。

相较于国外大量的理论和实证研究，国内学者很少有关于通货膨胀惯性及其变动特征的研究。刘金全和郑挺国(2007)分别以通货膨胀率和加速通货膨胀率为门限变量研究通货膨胀的结构转变，发现通货膨胀率持续性变强的特征［14］;张成思(2008)基于格点Bootstrap方法的研究发现，我国通货膨胀具有相对强的持续性［15］;苏梽芳(2010)应用自回归模型对我国通货膨胀持续性系数进行滚动样本估计以考察通货膨胀持续性动态特征，发现无论是通货膨胀期间或者通货紧缩期间，都表现出强烈的持续性特征［16］。

总结现有研究文献可以发现，已有的经验研究一般采用门限回归、平滑转移模型或者马尔科夫机制转换模型等模型来分析通货膨胀的持续性行为，Lima等人(2008)将此类模型称为对称影响模型，认为此类模型对于讨论不同通胀水平下的通货膨胀持续性行为仍存在局限性［17］。Koenker和Xiao(2006)提出的分位数自回归模型(Quantile Autoregression Model)则较好地解决了这一问题，这是因为，分位数自回归模型考察的是被解释变量的条件分布。除此之外，在分析通货膨胀持续性时，现有研究方法一般仅假定价格序列在样本期内要么为稳定状态、要么为非稳定状态，因而无法处理在不同时间段价格序列的稳态性质发生改变的情况。Koenker and Xiao(2004)提出的分位数单位根检验方法则适用于通货膨胀序列在某些时间段为稳态、某些时间段为非稳态的情形［19］。因此，本文在研究中国通货膨胀持续性的非对称特征时使用的是分位数自回归模型和分位数单位根检验方法。

二、计量模型

构建一个如下形式的p阶自回归模型，yt为被解释变量，ut为随机扰动项，如式(1):

将式(1)改写为如下的ADF函数:

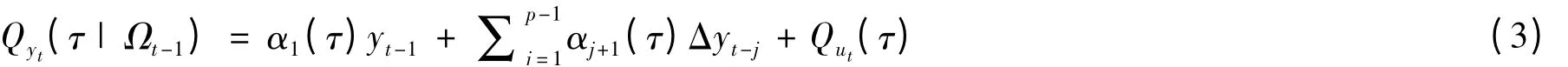
Ωt为{ys，s≤t}所集合而成的一个σ域，Qut(τ)为第τ个分位点。p阶分位数自回归模型如式(3)所示。令α0(τ)=Qut(τ)，α(τ)=(α0(τ)，α1(τ)，…，αp(τ))，xt=(1，yt－1，Δyt－1，…，Δyt－p+1)'，可以将式(3)改写成如下形式:

系数α(τ)=(α0(τ)，α1(τ)，…，αp(τ))的估计可以采用Koenker和Bassett(1978)提出的分位数回归方法，该方法的参数估计可以通过解如下的优化问题而得到:

此处，ρτ(u)=u(τ－I(u＜0))，I(u＜0)为示性函数，当{u＜1}时该函数取1，否则取0，采用线性规划办法得到估计值^α(τ)，并构建如下的分位数单位根检验的原假设:

上述原假设成立则意味着存在分位数单位根。我们可以使用如下的t统计量来检验yt在每一分位点上α1(τ)=1的原假设是否成立:

此外，上述单位根检验方法只是分析在某一特点分位点上的单位根检验，有时我们还希望知道在整个序列的所有分位点上是否存在单位根，为此，使用分位数Kolmogorov-Smirnov检验(QKS)进行检验［19］，该检验统计量如下:

此处，tn(τ)如式(7)所定义。在实际运用中，我们可以先取不同的分位数，计算每个分位数的tn(τ)(绝对值)，然后再从这些tn(τ)中取最大值。由于tn(τ)与QKS检验的大样本分布为非标准分布且受冗余参数的影响，我们可以利用bootstrap来估计检验统计量的小样本分布，其具体步骤如下所示:

(1)以普通最小二乘法(OLS)估计Δyt的p阶自回归模型:

取得估计值^βj，j=1，2，…，p以及残差。阶次p可利用AIC或BIC等信息准则来挑选。

(3)在单位根的零假设下，根据下式生成Δy*t的bootstrap样本:

(5)根据

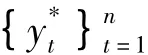
(6)重复步骤(2)到(5)多次，得到tn(τ)*和QKS*的经验分布，以此作为tn(τ)和QKS在原假设成立下的近似分布。

三、实证分析

(一)数据与描述性统计分析

在通货膨胀水平测度的多种指标中，本文采用应用最广泛的居民消费价格指数。同时使用月度同比增长率数据，避免了季节波动，也保证了数据的可得性，用cpi表示。样本从1990年2月到2013年4月，共279个数据，数据来源于和讯宏观数据网。图1显示了1990年以来我国月度cpi的动态变化趋势。从图1可以看出，1990年至今，我国通货膨胀的变动可以划分为两个阶段:1998年前，通货膨胀经历了一个长区间的大幅度上涨和下跌，通货膨胀持续性特征明显;而1998年后，通货膨胀的波动幅度虽然降低，但波动的时间区间变短，物价的升降交替频率在提高。通货膨胀的这一变动特征与我国的货币政策密切关联，总体上，我国货币政策可以1997年作为分界线。1997年之前的货币政策主要在反通货膨胀的主要目标下呈现出抑制需求的特征;而之后货币政策的主要目标发生转变，由反通货膨胀转变为反通货紧缩及促进经济增长，并表现出扩大需求的特征。为了更深入分析不同阶段中国通货膨胀持续性的特征，我们以1998年为分界点，将总样本划分为两个子样本，分别为1990年2月—1997年12月、1998年1月—2013年4月。表1给出了全样本和两个子样本的描述统计。

图1 中国通货膨胀水平的时间序列图(1990.1－2013.4)(单位:%)

表1 通货膨胀率的描述性统计

由表1可以看出，在全样本上，偏度系数大于0，峰度系数大于3，呈现出显著的尖峰厚尾特性;在两个子样本上，都呈现出一定程度的右偏。此外，JB统计量结果表明，无论是在整个区间上还是在两个子样本上，通货膨胀都不服从正态分布。

(二)实证分析

根据描述统计可知，通货膨胀不论是在全区间还是两个子区间上，都有较为显著的尖峰厚尾特征，且不服从正态分布，在这种情形下，与传统的单位根检验方法相比，分位数单位根检验方法具有更好的检验能力。但该检验的检验统计量不具有标准分布，这是由于受到数据非平稳性和冗余参数的影响，基于这一点，我们利用bootstrap方法，分别对全样本以及两个子样本的通货膨胀序列，进行重复抽样2000次，得到用于检验分位数的单位根检验统计量tn(τ)的临界值以及用于检验整个分位数过程上的单位根检验统计量的QKS临界值，结果如表2所示。

根据表2的临界值，表3给出了在各个分位点下通货膨胀率持续性的分位数自回归估计和分位数单位根检验的结果，其α1(τ)为自回归模型中自回归系数的总和。表3显示，在全样本上，α1(τ)的估计值区间为［0.948，1.020］，均值为0.984;在第一个子样本、第二个子样本上α1(τ)的估计值区间分别为［0.953，0.997］，［0.858，0.980］，其均值分别为0.982和0.942。由此可见，α1(τ)的估计值无论是基于全样本还是子样本，都非常接近1，说明中国的通货膨胀率的持续性很高，这反映了我国货币政策的滞后效应非常显著，通货膨胀对政策变化的反应速度缓慢。

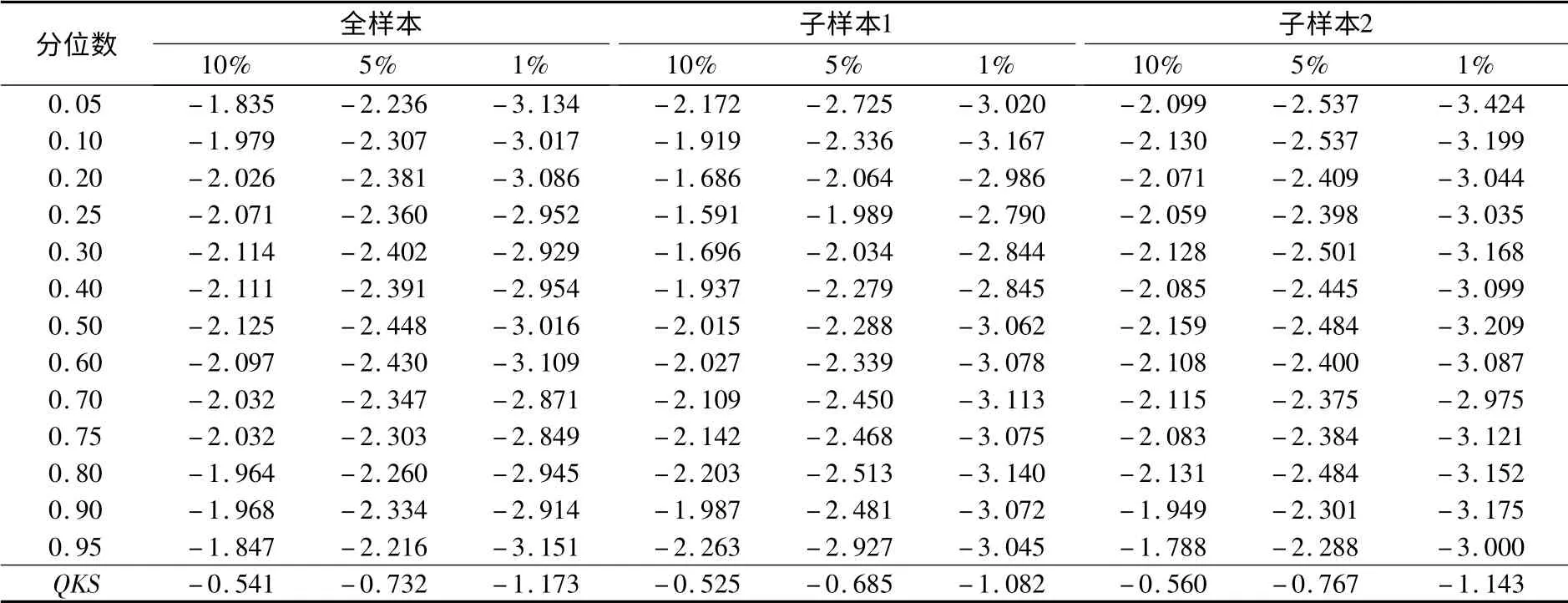
表2 分位数单位根检验临界值表

表3 通货膨胀水平的分位数单位根检验

接下来我们对系数α1(τ)进行单位根检验，检验统计量tn(τ)的估计结果如表4所示。对于全样本，当分位数小于等于0.6时，拒绝存在单位根的原假设，通货膨胀序列是平稳的;当分位数大于等于0.7时，不能拒绝存在单位根的原假设，认为通货膨胀序列是非平稳的;也就是说，当通货膨胀水平较低时，通货膨胀序列是平稳的，而当通货膨胀水平较高时，通货膨胀序列是非平稳的。在第二个子样本上，通货膨胀序列分别表现出平稳性和非平稳性特征。但是，在第一个子样本上，在所有分位点上，通货膨胀序列都是非平稳的。

上述分位数单位根检验是针对各个分位点进行的，我们同样可以由式(8)的QKS统计量来检验通货膨胀序列在所有分位点上是否存在单位根，QKS统计量的估计结果如表3最后一行所示。该估计结果显示，在全样本和第一个子样本上，通货膨胀序列具有单位根，而在第二个子样本上，通货膨胀不具有单位根。

我们还可以利用半衰期来进行通货膨胀持续性检验。基于分位数自回归模型计算的通货膨胀半衰期结果在表4列出。根据表4结果所示:第一，在不同分位点上，通货膨胀半衰期不同，说明通货膨胀持续期在不同分位点上的表现有别。第二，在所有分位点下，全样本和第一个子样本的半衰期均远远高于第二个子样本上的分位点，其中第一个子样本在所有分位点上的半衰期都为无穷大，表现出显著的通货膨胀持续性，而第二个子样本在0.05的分位点时其半衰期仅仅为4.54个月，说明在该分位点下，外生冲击对通货膨胀的影响在4个半月之后即可下降一半;总体来看，1998年之前的通货膨胀持续性要强于1998年之后的通货膨胀持续性。第三，除了全样本上的0.05分位点，在所有其他分位点上，通货膨胀的半衰期都随分位点的上升而增加，说明通货膨胀水平越高，通货膨胀的持续性越强。上述基于半衰期的研究结果再次验证了基于α1(τ)估计值的研究结果，即中国的通货膨胀持续性存在显著的非对称特征:1998年之后通货膨胀持续性低于1998年之前;低通货膨胀水平上的通货膨胀持续性要低于高通货膨胀水平上的。

表4 半衰期的计算结果

四、结束语

通货膨胀持续性是货币政策制定和实施的重要影响因素之一，而当前国内学界在研究通胀持续性时定量分析相对较少，既有的少量研究常基于自回归模型、机制转换模型和平滑转移模型展开，只能判断前期通货膨胀水平对当前通货膨胀水平所产生的平均作用。事实上，由于所处的国际以及国内宏观经济环境、外部冲击等因素存在巨大差异，通货膨胀的持续性可能发生变动，即存在非对称效应，对这种非对称效应的定量描述显然比仅仅检验通货膨胀是否存在持续性能提供更多的信息。本文以1990年2月—2013年4月的中国月度CPI数据为样本，利用分位数单位根检验方法和分位数自回归模型深入探讨了中国通货膨胀持续性的非对称特征;通过分析不同分位点上的α1(τ)值、单位根检验和半衰期，得到了稳健的结果:中国的通货膨胀持续期存在明显的非对称特征，1998年后通货膨胀持续性要显著低于1998年前;低通货膨胀水平上的通货膨胀持续性要显著低于高通货膨胀水平上的持续性。

我们的研究结论对货币政策的制定和实施给出了明确的政策含义:第一，因为通货膨胀持续性在不同通货膨胀水平下呈现不对称特征，所以货币当局制定实施货币政策时应根据具体的通货膨胀率进行调整。第二，通货膨胀率的稳态性质可能在不同时间段上发生变化，而并不一定总是处于稳定或非稳定状态，所以，外部冲击对通货膨胀产生的作用可能也不尽相同，外部冲击的作用会随通货膨胀处于何种水平而改变，例如，当通货膨胀水平较低(分位数较小)时，外部冲击对经济一般为暂时性影响，也就是所产生的作用较小;而在通货膨胀水平较高(分位数较大)时，外部冲击对通货膨胀所产生的冲击会持续很长时间，此时以降低通货膨胀为目标的货币政策应当适时地提高强度。总之，当通货膨胀水平受到外部冲击时，货币当局在制定实施货币政策在应考虑当时具体的通货膨胀水平基础上进行调整，方能达到维持物价稳定的目标。

［1］Fuhrer，J．and G．Moore．Inflation persistence［J］．Quarterly Journal of Economics，1995，110(1)，pp．127－159．

［2］Phelps，E．S．Disinflation without recession:Adaptive guideposts and monetary policy［J］．Review of World Economics，1978，114(4)，pp．783－890．

［3］Taylor，J．B．Aggregate dynamics and staggered contracts［J］．The Journal of Political Economy，1980，88(1)，pp．1－23．

［4］Roberts，J．M．Inflation Expectations and the Transmission of Monetary Policy［R］．Finance and Economics Discussion Paper，No．43，Board of Governors of the Federal Reserve System，1998．

［5］Mankiw，N．G．and R．Reis．Sticky Information versus sticky prices:A proposal to replace the new keynesian phillips curve［J］．The Quarterly Journal of Economics，2002，117(4)，pp．1295－1328．

［6］Taylor，J．B．Low inflation，pass-through，and the pricing power of firms［J］．European Economic Review，2000，44(7)，pp．1389－1408．

［7］Stock，J．H．Evolving Post-World War II USInflation Dynamics:Comment［R］．NBER Macroeconomics Annual，2001，16，pp．379－387．

［8］Pivetta，F．and R．Reis．The persistence of inflation in the United States［J］．Journal of Economic Dynamics and Control，31(4)，pp．1326－1358．

［9］Kumar，M．S．and T．Okimoto．Dynamics of persistence in international inflation rates［J］．2007，39(6)，pp．1457－1479．

［10］Lee，H．Y．and J．L．Wu．Mean reversion of inflation rates:Evidence from 13 OECD countries［J］．Journal of Macroeconomics，2001，23(3)，pp．477－487．

［11］Levin，A．T．and J．M．Piger．Is Inflation Persistence Intrinsic in Industrial Economies?［R］．the Federal Reserve Bank of St．Louis，Working Paper，2004．

［12］Cuestas，J．C．and B．Harrison．Inflation persistence and nonlinearities in central and eastern European countries［J］．Economics Letters，2011，106(2)，pp．81－83．

［13］Gadea，M．D．and L．Mayoral．The persistence of inflation in OECD countries:A fractionally integrated approach［J］．International Journal of Central Banking，2006，2(1)，pp．51－104．

［14］刘金全，郑挺国．我国通货膨胀率均值过程和波动过程中的双长记忆性度量与统计检验［J］．管理世界，2007，(7)，14－21．

［15］张成思．中国通胀惯性特征与货币政策启示［J］．经济研究，2008，(2)，33－43．

［16］苏梽芳．中国通货膨胀持续性事变特征及其来源分析［J］．云南财经大学学报，2010，(5)，34－39．

［17］Lima，L．R．，W．P．Gaglianone，and R．M．B．Sampaio．Debt ceiling and fiscal sustainability in Brazil:A quantile autoregression approach［J］．Journal of Development Economics，2008，86(2)，pp．313－335．

［18］Koenker，R．and Z．Xiao．Quantile Autoregression［J］．Journal of the American Statistical Association，2006，101(475)，pp．980－990．

［19］Koenker，R．and Z．Xiao．Unit root quantile autoregression inference［J］．Journal of the American Statistical Association，2004，99(1)，pp．775－787．

［20］Koenker，R．and G．Bassett．Regression quantiles［J］．Econometrica，1978，46(1)，pp．33－50．