高炉炉墙探测棒的传感器布设研究*

贾 华，王 浩，董大明，王月明，陈智辉

(1.内蒙古科技大学 信息工程学院，内蒙古 包头014000;2.内蒙古科技大学 数理生学院，内蒙古 包头014000)

0 引 言

高炉炉腹到炉身下部的炉墙寿命是限制现代大型高炉长寿主要环节［1］。根据高炉生产实践和科学研究表明，炉腹到炉身下部受到高温的化学侵蚀、氧化、机械磨损以及高强度的热流冲刷是影响高炉长寿的重要因素［1，2］，如何确保现代高炉的长期稳定运行，其中关键技术在于高炉炉墙温度的实时监测技术。基于这个问题，本文建立了一种内嵌探测棒的高炉炉墙温度与炉墙厚度的在线监测模型。通过仿真实验得出了探测棒在不同高炉炉墙厚度时的温度场分布情况，分析了探测棒在相同的加载条件下、不同高炉炉墙厚度时温度场的变化规律，跟据相关评价指标确定传感器在探测棒上的数量和传感器的布设方式。实现了实时准确测量探测棒的温度场分布情况，结合探测棒的实时长度进而推算出高炉炉墙的温度场分布情况，最终为指导高炉的正常运转和保证高炉长寿奠定了基础。

1 模型的建立

1.1 计算模型

以国内某高炉炉腹到炉身下部的高炉炉墙结构为原型，模型主要由6 部分组成:耐火粘土砖、镶砖、冷却壁、填充层、炉壳钢板以及探测棒(不考虑炉壁挂渣)。图1为探测棒与冷却壁的相对位置结构示意图，即在高炉相邻的四块冷却壁中间添加一根圆柱形探测棒，探测棒四周与冷却壁之间是以Si3N4-SiC 砖［3］为耐火材料的镶砖。为方便对模型进行热分析，本文对模型进行了简化，图1 虚线框中的部分为简化后的仿真计算模型所在区域，简化后的二维仿真模型结构图如图2 所示，仿真模型采用长度比例为10︰5︰8(长(X):宽(Z):高(Y)的长方体结构，且高炉炉墙结构以探测棒中心线上下对称。如图所示，靠近耐火粘土砖的是受到高温作用的高炉炉墙内表面，而靠近炉壳钢板的是与空气直接接触的高炉炉墙外表面。

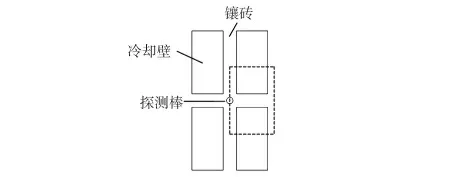
图1 探测棒与冷却壁的相对位置Fig 1 Relative position of wand and staves

图2 二维仿真模型结构示意图Fig 2 Diagram of two-dimensional simulation model

1.2 稳态温度场计算前提条件

假设炉墙热面附近炉气温度、冷却水温度和炉墙冷面空气温度都保持不变;由于在高炉炉腹到炉身下部处高炉内部环境恶劣，忽略高炉内壁挂渣的存在［4］;忽略炉壳、填充层、铜冷却壁、镶砖、砖衬以及探测棒之间所有可能的接触热阻和砖缝的热阻;当高炉炉墙的耐火材料被完全侵蚀后，在高温下的化学侵蚀、机械磨损以及热流冲刷等恶劣的环境下，设定探测棒周围的镶砖被侵蚀程度保持同步。

1.3 稳态温度场计算

高炉在正常工作时，炉内温度工况和炉墙内温度分布可近似为稳态温度场，通过炉墙的导热可近似看做稳态导热。其三维导热微分方程为

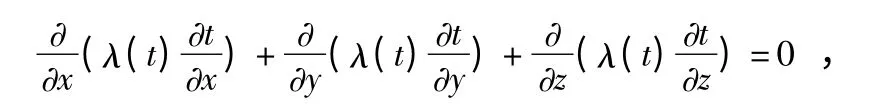
式中 x，y，z 为空间坐标;λ(t)为温度为t℃时的导热系数，W/(m·℃)。

该方程的定解条件为:

1)炉壳与空气之间的热交换有对流换热和辐射换热两种，在炉壳表面温度t1小于300 ℃时，其换热过程主要是以对流换热为主，其综合对流换热系数h1为［5］h1=9.3+0.058t1.

本文计算时取t1=40 ℃，这时高炉炉墙冷面的对流换热系数为h1=11.62 W·m－2·℃－1.

2)炉墙热面与煤气流之间的热交换属于第三类边界条件，炉内煤气流与炉墙的综合对流换热系数h2为［5］:h2=232W·m－2·℃－1，此时，假设炉内煤气流的温度t2=1 200 ℃。

3)冷却水与铜冷却壁之间的对流换热系数h3为［6］

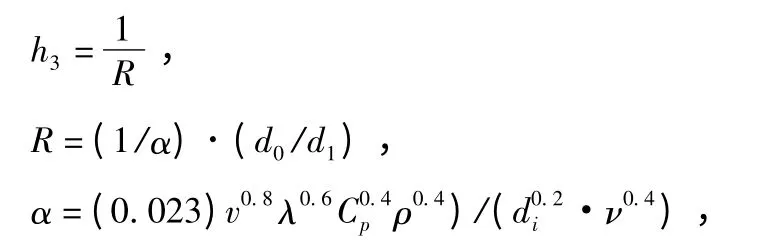
式中 R 为冷却水管内表面与水的对流换热热阻;α 为强制对流换热系数;d0，di为分别为冷却水管的外径和内径，且d0=di;v，λ，Cp，ρ，ν 分别为冷却水的水速、导热系数、比热容、密度及粘度。

2 计算结果与分析

通过上述理论与数据建立仿真模型并对其进行数值仿真，为了对比分析不同高炉炉墙厚度时探测棒温度场的分布情况，高炉炉墙厚度z 分别设定为:5.0，4.7，4.4，4.1，3.8，3.5，3.2，2.9，2.6 dm 九种不同的高炉炉墙厚度，也就是每当有0.3 个单位的高炉炉墙内表面被侵蚀时，对其进行一次仿真实验，从而获得不同高炉炉墙厚度时探测棒的温度场分布图。如图3 所示为高炉炉墙厚度为z=4.1 dm时探测棒的温度场分布图。

图3 在高炉炉墙厚度为z=4.1 dm 时探测棒的温度场分布图Fig 3 Distribution image of temperature field of wand when z=4.1 dm(z is thickness of blast furnace wall)

从图3 不难看出:温度主要沿探测棒的轴线方向变化，纵向方向的温度变化较小，所以，选用探测棒中轴线上各节点的温度变化曲线来分析探测棒的温度变化规律。如图4 为探测棒在不同炉墙厚度时中轴线的温度变化曲线，比较不同高炉炉墙厚度时探测棒中轴线温度变化曲线不难发现:1)探测棒中轴线上各节点温度随着与热面距离的增大而减小;2)探测棒上某一点的温度值随着高炉炉墙厚度不断被侵蚀而逐渐升高;3)在不同高炉炉墙厚度时，探测棒中轴线温度变化趋势符合热传递的基本规律。但是根据探测棒温度场分布图和探测棒中轴线温度变化曲线并不能确定传感器的布设位置和传感器的布设数量。下面通过探测棒中轴线温度变化曲线的距离等差、温度等差以及温度中位数来确定传感器在探测棒上的布设位置和传感器布设数量。其中，等差选点是以探测棒冷端为起点，每经过一定距离或一定温度选择一点为传感器布设点，温度中位数选点是选择温度数列中间点为传感器布设点。

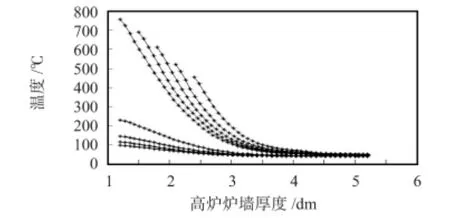
图4 不同高炉炉墙厚度时探测棒中轴线的温度变化曲线Fig 4 Temperature variation curve of axis of wand on blast furnace wall of different thickness

图5 分别为三种选点方案的最大温度误差、平均温度误差以及选点数量折线图，其中，距离等差选点公差d=0.05 dm;温度等差选点公差t=45 ℃，选择高炉炉墙厚度z=3.8 dm时的探测棒中轴线温度变化曲线作为基本研究对象，并按照高炉炉墙厚度z=3.8 dm 时的探测棒选点对其他厚度的中轴线进行同样位置的选点;为避免温度变化对选点的影响，采用探测棒中轴线温度中位数来确定选点的位置，同样选择高炉炉墙厚度z=3.8 dm 时的探测棒中轴线温度变化曲线作为基本研究对象，并对其他厚度的中轴线进行同样位置的选点。

如图5(a)所示为三种选点方案的最大温度误差选点图，从图中可以看出:当高炉炉墙厚度从5.0 dm 降到2.6 dm时，温度等差选点的最大温度误差从2.0 ℃升高到49.1 ℃，距离等差选点与温度中位数选点的最大温度误差也达到20 ℃左右。在高炉炉墙厚度为z=2.9 dm 时，探测棒最高温度仅为114.5 ℃、最低温度为40.6 ℃，而温度等差选点的最大误差达到34.2 ℃，显然温度等差选点误差太大。如果增大t 值，只会使曲线之间的误差变得更大，而探测棒上选点数量变化却并不明显;如果减小t 值，探测棒上的选点数量将会大于12，与理想探测棒传感器布设数量差距较大，所以，减小t 值同样不能得到理想的传感器布设位置。图5(b)为三种选点方案的平均温度误差选点折线图，温度等差选点的平均温度误差在不同炉墙厚度时均大于其他两种选点方式的平均误差，结合图5(c)中选点数量折线图可以明显得出:距离等差和温度中位数选点优于温度等差选点。

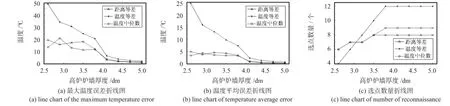
图5 三种选点方案的最大误差、平均误差以及选点数量折线图Fig 5 Line chart of the maximum error，average error and number of reconnaissance of three kinds of reconnaissance plans

比较距离等差选点与温度中位数选点折线图不难发现，在不同高炉炉墙厚度时，温度中位数选点与距离等差选点的最大温度误差、平均温度误差之间的差距不超过6 ℃，且两者选点数量最多相差一个。结合高炉实际运行情况可知，高炉炉腹到炉身下部受到高温下的化学侵蚀、氧化、机械磨损以及高强度的热流冲刷，使得高炉炉衬在高炉运行前期就被侵蚀殆尽，高炉运行后期主要依靠冷却壁的冷却能力来保证高炉炉墙的温度，即在高炉炉墙厚度z=2.6 dm时，温度测量误差将会直接影响高炉后期的运行状况，甚至影响高炉的服役寿命。所以，在高炉炉墙厚度为z=2.6 dm时，拥有较低的最大温度误差和平均温度误差的温度中位数选点优于距离等差选点。如果d=0.35 dm 时，曲线最大温度误差减小为12.2 ℃，但探测棒上的选点数量将增加到11 个，如果将温度中位数选点数量增加到11 个时，曲线的最大温度误差仅为10.2 ℃，且在高炉炉墙厚度z=2.6 dm时，其最大温度误差值与平均温度误差仍然小于距离等差选点时的最大温度误差与平均温度误差。如果继续减小d的取值，曲线之间的误差会明显减小，但探测棒上的选点会明显增多，这将会增加探测棒的制作成本，所以，继续减小d 的取值并不可取。综合比较上述三种选点方案得出:温度中位数选点优于其他两种布设方式。

为得到理想的传感器布设方案，下面对温度中位数选点进行优化布设，即在误差较小的区域删除选点，而在误差较大的区域增加选点。如图6 为优化后的温度中位数最大温度误差、平均温度误差以及选点数量折线图。可以看出，在不同高炉炉墙厚度时，曲线的平均温度误差均低于2.4 ℃、曲线最大温度误差均小于8 ℃、探测棒的选点数量为9 个，且优化后的各个指标均小于图5 中三种选点方式。如果将选点的折线与原探测棒中轴线温度曲线在各点的温度差与原探测棒中轴线的温度值比值定义为T，当T 小于等于5%时称该点命中，通过计算可以知道，优化后选点方式的命中率大于95%。所以，优化布设后的温度中位数选点可以实现实时准确测量出探测棒的温度场分布情况，结合探测棒长度数据进而推算出高炉炉墙的温度场分布情况，最终实现指导高炉的正常运转和保证高炉长寿的目的。

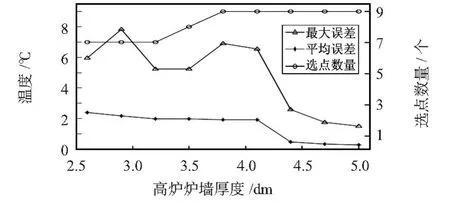
图6 优化后的温度中位数最大误差、平均误差以及选点数量折线图Fig 6 Line chart of the maximum error，average error and number of reconnaissance of the optimized temperature median

3 结 论

根据高炉实际尺寸和结构建立仿真模型并对其进行数值仿真，通过仿真实验数据得到了不同高炉炉墙厚度时探测棒中轴线温度变化曲线。在探测棒中轴线温度变化曲线的基础上，对比分析三种传感器布设选点方案发现:温度中位数选点优于其他两种布设方案。对温度中位数选点进行优化布设后，其命中率大于95%，误差满足生产工艺要求，对提高探测棒温度曲线精度、准确预测探测棒的温度场分布情况发挥了有效作用。

［1］ 程树森，杨天钧，左海滨，等.高炉炉身下部及炉缸、炉底冷却系统的传热学计算［J］.钢铁研究学报，2004，16(5):10－13，23.

［2］ 郑建春，宗燕兵，苍大强.高炉铜冷却壁热态试验及温度场数值模拟［J］.北京科技大学学报，2008，30(8):938－941.

［3］ 张寿荣，于仲结.武钢高炉长寿技术［D］.北京:冶金工业出版社，2009.

［4］ 佘京鹏，陈 钢，许领舜，等.对高炉铜冷却壁应用特性的几点认识［J］.炼铁，2013，32(4):22－27.

［5］ 薛国庆，高小武，程素森.冷却壁高炉炉墙温度场的数值模拟［J］.北京科技大学学报，2000，22(2):127－130.

［6］ 程素森，薛国庆，苍大强，等.高炉冷却壁的传热分析［J］.北京科技大学，1999，34(5):11－13.