基于激光位移传感器的小转角测量方法研究*

魏聚周，何柏岩，方永刚

(1.天津大学 机构理论与装备设计教育部重点实验室，天津300072;2.西安空间无线技术研究所，陕西 西安710000)

0 引 言

结构在小扭矩作用下的转角测量工作是结构刚度测试中的重要环节。为保证结构不致因过大加载发生破坏，结构发生的转角通常不会太大，属于小转角测量的范畴。传统的机械式和电磁式的测角技术，因易受测量环境和操作者的影响，其测量精度受到限制［1］。光学测角的方法以其灵敏度高、准确度高的特点在实际生产中的应用越来越广泛。目前常用的光学测角方法有自准直法、全内反射差动探测法、干涉法等。其中，文献［2］改进了迈克尔逊干涉仪的结构，并基于该方法实现了物体的微小转角测量。文献［3］把光栅楔形平板用于双频激光干涉转角测量中，代替了干涉系统中的部分角锥棱镜，减小了干涉仪的尺寸。文献［4］利用单缝衍射分离间隙法，通过拟合得到衍射条纹位置，反求出转角的变化。虽然以上光学测转角方法均能达到较高的测量精度，但是工作原理复杂，调试繁琐，对元器件的加工精度要求甚高。此外，李立春等人［5］采用高分辨率相机采集被测物上长直线标志，通过高精度检测图像上直线的倾斜角度来计算转角，但该方法具有后续工作量大的缺陷。

基于光学三角法原理［6］工作的激光位移传感器，能实现非接触在线测量位移、物体表面形貌、振动等［7～9］。激光位移传感器的应用日趋广泛，但大多是针对物体线位移的测量。本文提出了一种把激光位移传感器所测位移转换成转角的方法，具有易于装夹，安装距离小的特点，且能够实现对结构微小转角的非接触、动态测量。该方法拓宽了激光位移传感器的应用领域，并丰富了微小转角测量的理论和方法。

1 测量原理

图1 为某工件扭转刚度测试时的转角测量装置示意图，主要由试验机、待测工件、激光位移传感器、传感器支座组成。通过试验机夹头夹紧待测工件，调节传感器支座高度和位置，使得安装在其上的激光位移传感器发出的光束，垂直照射在随待测工件一起转动的平直表面上。为方便描述，将用于激光照射的平直表面称为光照表面，将过旋转轴线且平行于光照表面的平面称为理想光照表面。光照平面可由工件本身具备的平直表面充当(图2(a))。若待测工件不具备这样的表面，则需要设计具有平直表面的辅助结构，通过相应的连接方式固定在待测工件上。如图2(b)所示，采用夹具夹持待测工件，并将具有平直表面的辅助结构固定在夹具上，从而实现辅助结构与工件的固定连接。在光照表面上作一竖直刻线标志(图1)，在安装传感器时，应保证光束垂直照射在刻线处。

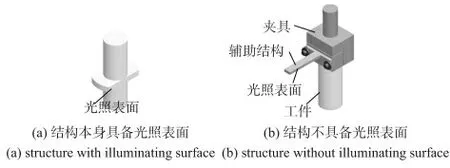
图2 光照表面Fig 2 Illuminating surface

图3 所示为测量原理图，图中虚线表示理想光照表面。当工件处于初始位置时，点A'代表光束在光照平面上形成的光斑(与刻线投影重合)，其在理想光照平面上的投影(A点)到旋转轴线的垂直距离记为l0。当工件发生角位移θ时，光束与理想光照平面相交于点B，B'为此时的光斑位置，A'B'即为激光位移传感器所测得的线位移，记为s。在θ较小的情况下，A'B'与AB 近似相等，在△OAB 中，利用反正切近似求出此时的角位移θ

由于目前激光位移传感器大都具有较高的采样频率，因此，在测量高频下的动态角位移时，本方法也能胜任。同时也适用于其他定轴转动情况下的角位移测量。

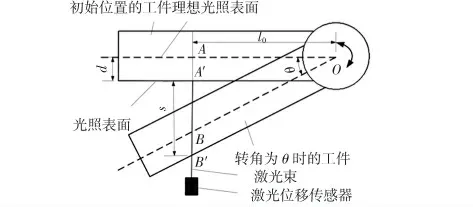
图3 测量原理Fig 3 Measuring principle

2 测量误差分析

2.1 误差来源分析

本文所提出的测转角方法，其误差主要来源于以下几个方面:

1)如图3 所示，激光位移传感器所测位移s 与线段AB长度之间存在偏差，这是由光照表面与理想光照表面的垂直距离d 造成的;

2)如图4 所示，在实际安装激光位移传感器时，若光斑与刻线存在对准误差Δl，采用式(1)计算得到的转角必然存在误差;

3)工件在初始位置时，若光束与光照平面法线方向不重合，即光线与x 轴具有夹角α(图4)，测量结果也会产生误差。该夹角可以用两个相互独立的角度(α1，α2)表示出来，其中，α1，α2分别为实际光束在面xA'y 和面xA'z 内的投影与x 轴的夹角(图5)，因此，将α1，α2作为两个误差因素。

由于以上所述的误差因素皆是在传感器安装过程中产生的，因此，把它们统称为安装误差。

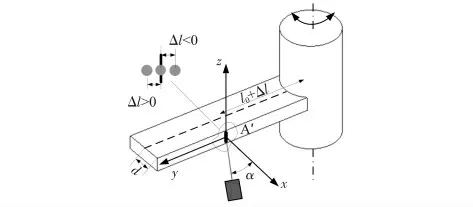
图4 误差分析示意图Fig 4 Diagram of error analysis

2.2 误差模型建立

对于图4 中所示的夹角，可看成光束先在面xA'y 内偏转一角度α1，再在此基础上俯仰一角度β 得到(图5)。由几何关系得到β 与α1，α2的关系

图6 为整个测量系统在xA'y 内的投影。当工件转过角度θ 时，传感器实际测得位移为s，投影到xA'y 内得s'=scos β。在△A'CD 中

图5 夹角分析示意图Fig 5 Diagram of included angle analysis

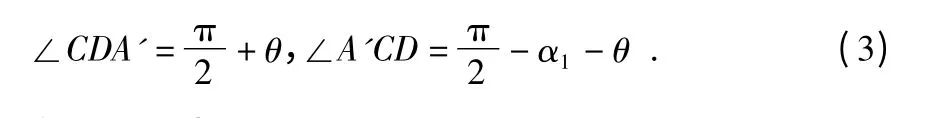
在△AEO 中

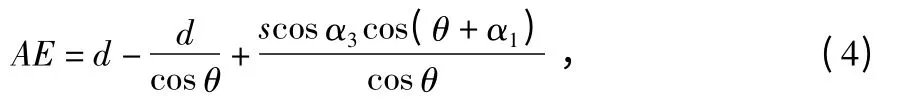
并有以下关系式

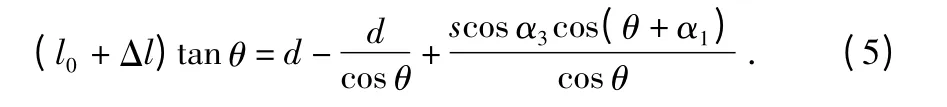
通过式(5)可以计算出转角的真实值。

规定待测工件逆时针旋转得到的转角为正。当θ ＞0时，解出θ

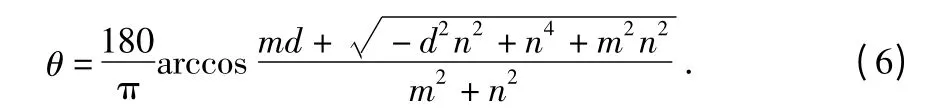
其中

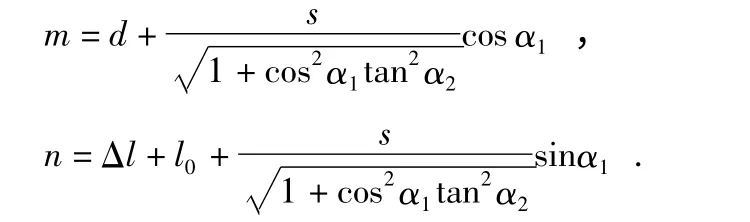
图6 测量系统投影到xA'y 面Fig 6 Measuring system projected onto surface of xA'y

当θ ＜0 时，s ＜0，只需将式(6)前加一负号就能得到θ真实值。

将采用式(1)计算出来的转角记为θ'，其与真实的角位移存在偏差，偏差大小为

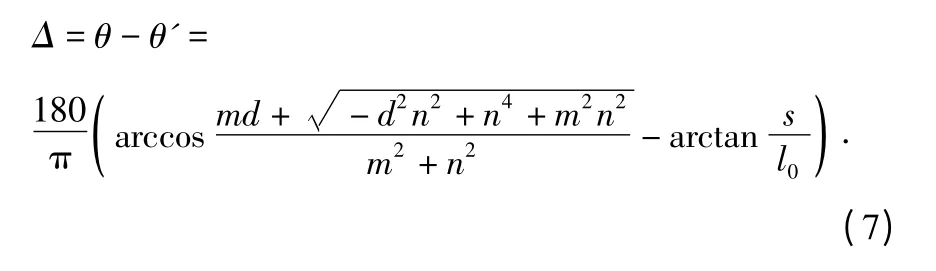
式(7)即为本测量方法的综合误差数学模型。

2.3 各误差因素对测量结果影响分析

显然，式(7)分别是4 个误差因素的强非线性函数，若分别对4 个因素求偏导，得到的解析算式将会非常复杂，因此，需采用数值方法分析各误差因素分别对测量结果的影响。不妨先确定以下参数值:l0=50 mm，转角范围为－1～1°，其余参数值如表1 所示。

表1 其余参数取值Tab 1 The rest of parameters values

各误差因素分别对测量结果的影响。如图7(a)～(b)所示，随着转角的增大，d 引入的测量误差有加快增大的趋势，但不超过0.1%。α1对测量结果的影响没有确定的规律，不过其引起的误差不超过0.15%(图7(c)，(d))。α2引入的测量误差与转角近似呈线性关系，但误差较小，几乎可以忽略不计(图7(e)，(f))。光斑与刻线标志的偏距Δl导致的测量结果误差与转角同样近似线性，其影响规模相对较大，当Δl 取±2 mm 时，误差接近4%，而当Δl 取±1 mm时，误差为2%左右(图7(g)，(h))。

3 测量应用实例

本实验待测工件是航天装备中的某类型铰链，在对其接头进行扭转刚度测试时，采用本方法获取转角值。由于铰链不具备用于激光照射的平直表面，因此，需开发相应夹具实现辅助结构与铰链的连接，图8 为试验现场图片。采用Instron8874 试验机施加扭矩，LK—G5000 型激光位移传感器采集位移值，采样频率100 Hz，加载时间4 min。由于选用的激光位移传感器采样频率最高可达392 kHz，因此在动态加载时，本方法也能胜任。

采用式(7)对测量误差进行评估，已知l0=51.3 mm，d=9.5 mm。由3.3 节知光斑与约定刻线距离Δl 对测量结果误差影响较为显著，考虑极限安装误差，取α1=α2=2°，分别作Δ l=0，±1 mm 时的误差曲线图(图9)。从该图中可以看到，在Δl=±1 mm 时，误差随转角增大而增大，且相对误差在2%左右;当Δl=0 时，由其他因素引起的误差较小，此处也间接证明了Δl 对测量结果影响较大的结论。

4 结 论

1)提出了一种采用线位移测量而间接实现角位移测量的方法。

2)分析了测量误差来源，建立误差数学模型，并分别进行了误差因素对测量结果影响的数值模拟分析，结果表明Δl 对测量结果影响较为显著。

3)采用本方法，对一异形铰链进行扭转刚度测试，在考虑极限安装误差的情况下，测量误差约为2%，验证了本文方法的有效性和正确性。

［1］ 孙方金.精密测角转台［J］.计量学报，1986，17(4):291－295.

图7 误差因素分别对测量结果的影响Fig 7 Effect of error factors respectively on measurement results

图8 试验现场Fig 8 Test site

图9 误差—转角曲线Fig 9 Curve of error vs rotation angle

［2］ Fang Chenga，Kuang-Chao Fanb.High-resolution angle measurement based on michelson interferometry［J］.Physics Procedia，2011，19:3－8.

［3］ 陶 卫，浦昭邦，张 琢.光栅楔形平板及其在转角测量中的应用［J］.光电子·激光，2002，13(4):371－377.

［4］ 花世群，骆 英，赵国旗.基于单缝衍射原理的小转角测量方法［J］.光电子·激光，2006，17(8):978－981.

［5］ 李立春，于起峰，雷志辉.基于数字图像的高精度面内转角测量方法［J］.光学学报，2005，25(4):491－496.

［6］ 王晓嘉，高 隽，王 磊.激光三角法综述［J］.仪器仪表学报，2004，25(4):601－604.

［7］ Yan Gao，Feng Qibo，Cui Jianying.A simple method for dynamically measuring the diameters of train wheels using a one-dimensional laser displacement transducer［J］.Optics and Lasers in Engineering，2014，53:158－163.

［8］ Jakub Sandak，Chiaki Tanaka，Tadashi Ohtani.Evaluation of surface smoothness by a laser displacement sensor II:Comparison of lateral effect photodiode and multi element array［J］.Journal of Wood Science，2004，50(1):22－27.

［9］ Miyasaka T，Okamura H.Dimensional change measurements of conventional and flowable composite resins using a laser displacement sensor［J］.Dental Materials Journal，2009，28(5):544－551.