伯川德竞争下供应链信息泄露问题的研究

李夏隆，王晓佳，2，冯南平，2

（1.合肥工业大学 管理学院，安徽 合肥 230009；2.安徽省产业转移与创新发展人文社科基地，安徽 合肥 230009）

0 引言

近十多年来，信息技术的发展极大地加强了企业之间进行信息共享的能力。供应链中各企业通过信息共享对市场进行更准确的预测以降低牛鞭效应，提高供应链绩效。然而信息共享过程中带来的信息泄露问题却严重影响了供应链成员共享信息的积极性，甚至会造成供应链合作关系的破裂［1］。比如音乐零售商NewBury Comics因唱片销售信息遭到泄露而中止了相关的信息共享作用，Wal－Mart公司因信息泄露问题宣布不再与第三方信息收集公司Information Resources Inc共享零售信息［2－3］。研究表明，信息泄露现象在各行各业都普遍存在着［3］。事实上，只要供应链存在信息流动和信息共享，信息泄露问题就有可能发生。因此，研究信息泄露问题对建立供应链良好的信息共享和信息管理机制，实现供应链的高效和协调运作具有重要意义。

关于信息共享在供应链所起到的作用，文献［4］通过大量的例子证明了供应链中的企业可以从共享需求信息和预测信息中获益。近十几年来，供应链中纵向企业之间的信息共享问题引起了人们的关注。文献［5］指出目前关于信息共享的研究主要集中在2个方面：一是信息对供应链绩效的提升价值；二是信息共享的机制。文献［6］指出供应链中若采用批发价格契约会导致需求预测信息扭曲。文献［7］的结论显示供应链进行库存信息共享能提升供应链的服务水平。

在供应链信息共享中信息泄露问题方面，文献［8］考虑了一个供应商和多个进行古诺竞争零售商的二级供应链，结果发现没有进行信息共享的零售商能从批发价格中推测出信息共享的内容。作者将这种现象定义为信息泄露问题，认为此类问题会削弱供应链成员进行信息共享的积极性。文献［9］将文献［8］的工作推广到了伯川德竞争下的情形。文献［10］考虑了相似的模型，并认为供应商通过与零售商共享信息，将信息泄露出去。文献［3］考虑了包含1个供应商和2个零售商的供应链下的信息管理问题，结果显示当供应链采取批发价格契约时，供应商总会泄露信息。文献［11］也考虑了相似的模型，加入了零售商的销售成本，得出信息泄露条件下零售商形成分离均衡和混同均衡的条件并进行了分析。文献［1］在文献［3］的基础上，探讨了收益共享契约对供应链信息泄露问题的作用，结论显示，一份设计合理的收益共享契约能有效防止信息泄露问题。文献［1，3，11］均考虑了存在策略性信息泄露下，零售商发生古诺竞争时的情形，但没有考虑伯川德竞争下的情形。

因此，考虑到价格作为一个重要的经济杠杆，本文探讨了伯川德竞争下供应链信息泄露的问题。与文献［3］相似，本文同样考虑了1个供应商和2个具有竞争关系的零售商的供应链，通过建立相关的信号博弈模型，探讨了供应链成员的决策，并给出零售商在分离均衡下的最优定价。本文的相关结论是在伯川德竞争方面对研究信息泄露问题的一个补充。

1 问题描述与模型

考虑包含1个供应商S和2个具有价格竞争关系的零售商R1和R2所组成的供应链（也可以是1个供应商和2个直接面向消费者的制造商），供应商S向2个零售商提供商品。零售商R1占据市场的主导地位，为主导零售商。零售商R2新进入市场，跟随主导零售商的策略进行决策，为跟随零售商。2个零售商面临具有需求不确定性的市场。

记号如下：、、分别为2个零售商的定价、需求和收益（i＝1，2）；、w分别为供应商的收益和批发价格；下标d＝H、L，表示此时市场需求为高（低）需求；E＝N、S，分别表示在不泄露信息和泄露信息下的情形。如表示不泄露信息和低市场需求下，主导零售商的定价。

1.1 需求函数

本文所研究的是，零售商之间面临的是伯川德竞争，即价格竞争。定义零售商面临的市场潜在需求为A，从而零售商所面临的需求函数为：

其中，0＜r＜1，r表示2个零售商所销售的商品的替代率，其销售的商品为不完全替代品。市场需求A是一个随机变量，存在2个可能值AH（高需求）和AL（低需求）［1，3，11］，2种需求出现的先验概率分别为p和1－p，平均市场需求为μ＝pAH＋（1－p）AL。2个零售商所面临的市场需求一般是有区别的，但为了简化模型，与文献［12］相同，仅考虑2个零售商在信息掌握方面的区别，故不加以区分。主导零售商具有市场需求的信息优势［1，3，11］，能事前观测出真实的市场需求。零售商的收益函数为：

供应商的收益函数为：

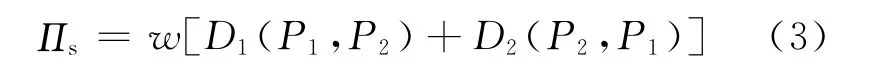
1.2 模型假设与事件发生顺序

模型基本假设如下。

H1：供应链所有成员都是风险中性和理性的，追求利益最大化。

H2：市场需求A的分布和需求函数D是供应链所有成员的共同知识。

H3：供应商不会有意编造主导零售商的信息［1］。

模型描述的问题中事件的发生顺序为：

（1）供应商制定批发价格w。

（2）主导零售商事前通过自身优势观察出市场需求A的真实值（AH或AL）。

（3）主导零售商和供应商进行信息共享和合作定价，确定零售价P1和需求D1，并向供应商订货。

（4）供应商可能会将主导零售商的定价信息透露给跟随零售商。

（5）跟随零售商确定零售价P2并根据需求D2向供应商订货。

（6）零售商的商品进入了市场，供应链的成员都知晓真实的市场需求A并实现自身的利益。

在事件（3）中，为了简化问题的考虑条件，假定零售商作为合作定价的主导者，淡化了供应商在合作定价中的直接作用，只强调供应商传递信息的作用。这类似于双渠道供应链中，供应商与零售商采取一致定价的情形。

2 模型分析

首先考虑供应商不泄露信息和泄露信息2种基准场景下，零售商的定价和收益；再分析供应商的决策和行为，发现当满足一定条件时，供应商总会泄露信息；最后考虑了供应商泄露信息时，主导零售商和跟随零售商的决策和分离均衡定价。

2.1 供应商不泄露信息

若供应商不泄露主导零售商的定价信息，跟随零售商并不清楚主导零售商的定价，此时零售商之间发生静态博弈。由（2）式，主导零售商在高市场需求和低市场需求的收益为：

而跟随零售商由于不清楚真实的市场需求，只能依据先验概率求出平均收益：

应注意的是，（6）式是平均收益，当市场需求为AH时，需求过剩，跟随零售商的收益与（6）式相同。而当市场需求为AL时，供给过剩，此时跟随零售商的实际收益为：

为了简便起见，不考虑产品的净残值，这并不影响主要结果。

通过对（4）～（6）式求一阶条件并联立求解得到零售商R1、R2的最优定价为：

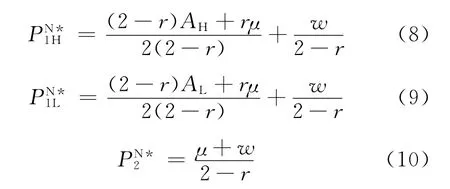
相应的需求为：

2.2 供应商泄露信息

若供应商总会泄露信息，跟随零售商则根据主导零售商的定价制定价格。假设主导零售商在不同的市场需求下制定不同的价格，则零售商之间发生一个完全信息的主从博弈。当市场需求为Ad时，由（2）式，零售商的收益函数为：

首先由主导零售商R1决定价格PS1d，然后跟随零售商R2根据PS1d决定价格PS2d，采用逆推法易得到R2对R1的价格反应函数为：

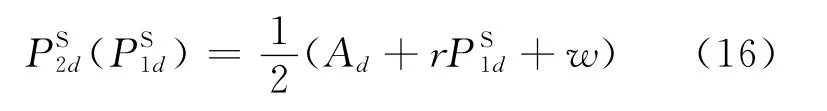
再将（16）式代（14）式，求其一阶条件，得到 R1、R2的最优定价：

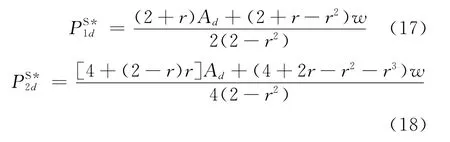
相应的需求为：

2.3 供应商决策行为分析

由于供应商是理性的，因此供应商是否泄露主导零售商的定价信息取决于采取哪种决策能增加自身的收益。通过对比供应商在2种决策下的收益，进而分析供应商的决策行为。为便于讨论问题，定义：

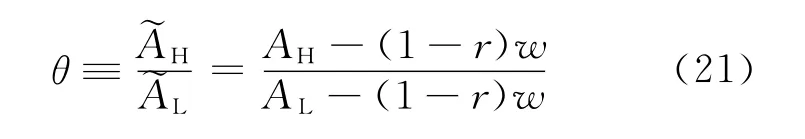
表示市场需求A的不确定性或AH与AL的相对差异程度。文献［1，3］也有类似的表示。

命题1当［4（1－p）＋r2（r＋2p－3）］θ＞（4－2r2）（1－p），供应商总会泄露信息。

证明当市场需求为AH，供应商不泄露信息时，其收益为：

而供应商泄露信息时，其收益为：

将（11）式、（13）式代入（22）式，（19）式、（20）式代入（23）式，并相减得到：

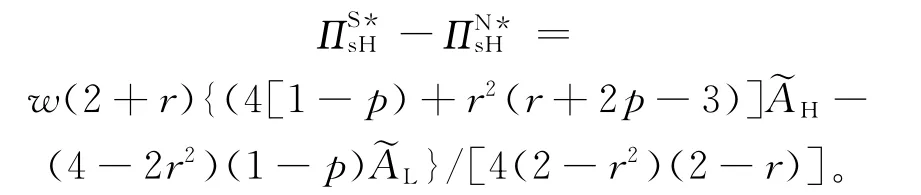
显然（2＋r）和分母4（2－r2）（2－r）都大于0，批发价格w也不会为0，而因式

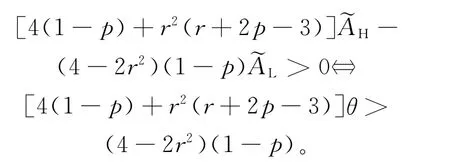
当市场需求为AL时，即便供应商不泄露信息，由于A的分布是共同知识，零售商R2也能从供应商不泄露信息的行为判断出市场需求为AL。综上，当满足命题1条件时，供应商会选择泄露信息增加其收益。命题1得证。

2.4 供应商泄露信息时的分离均衡

当满足命题1的条件时，供应商总会泄露信息，此时主导零售商会策略性地调整自己的定价，而跟随零售商也会将主导零售商的策略纳入自身决策之中。若主导零售商的定价足够高，则跟随零售商会认为此时是高市场需求；若定价足够低，则认为此时是低市场需求。因此，在信息泄露的条件下，零售商之间发生信号博弈。定价信号由主导零售商发出，通过供应商传递给跟随零售商。类似文献［1，3］，定义跟随零售商的信念为：

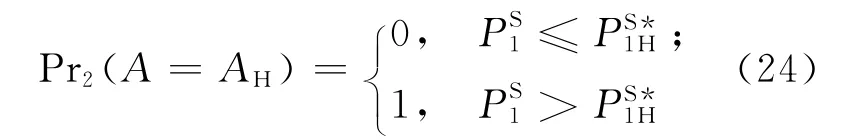
对于主导零售商，最主要的激励便是希望跟随零售商制定高价格，从而获益。在信息泄露的情况下，主导零售商可能在低市场需求时发出高市场需求的信号（即模仿高市场需求制定高价格），让跟随零售商相信是高市场需求，从而相应地制定高价格。但跟随零售商也会考虑到这一点，由信念（24）式确定市场需求。由于分离均衡的存在，应保证主导零售商的定价能反映出真实的市场需求，使得跟随零售商能正确判断市场需求类型。为便于讨论，根据市场需求的高低，将主导零售商分为高需求主导零售商和低需求主导零售商2种类型。考虑零售商分离均衡下的定价策略，得到命题2。

命题2当供应商总会泄露主导零售商的定价信息时，分离均衡下零售商的最优定价有2种情况。

（1）当市场需求为AL时，主导零售商的定价为：

当市场需求为AH时，主导零售商的定价为：

（2）当市场需求为AL，且Pr2（A＝AH）＝0，跟随零售商的定价为：

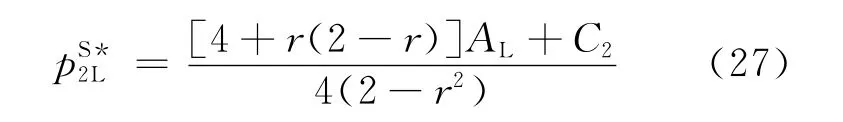
当市场需求为AH，且Pr2（A＝AH）＝1，跟随零售商的定价为：

其中

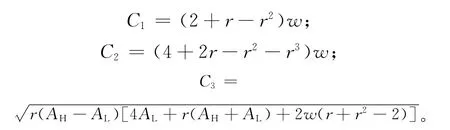
证明为了实现分离均衡，主导零售商的定价要能反映出真实的市场需求。主导零售商在分离均衡下的定价应满足的目标函数为：

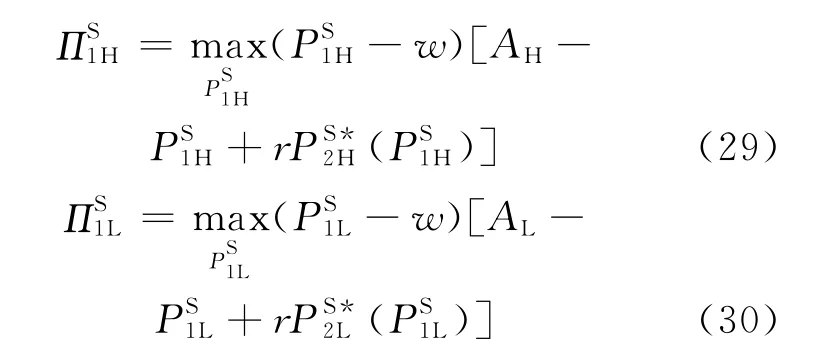
并满足激励相容条件：

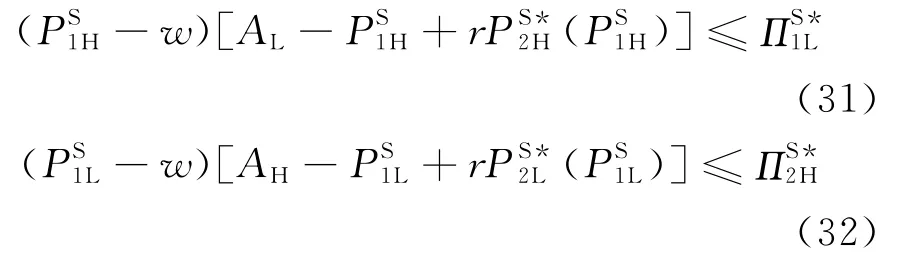
（31）式、（32）式是防止主导零售商混同市场需求，形成分离均衡的限制条件，即高（低）需求主导零售商不会混同低（高）需求主导零售商。然而只有低需求主导零售商存在混同市场的激励，故只考虑（29）式、（31）式。将（16）式代入（29）式、（31）式，并由（2）式、（17）式、（19）式得，最后得到目标优化问题：

对上述目标问题构造拉格朗日函数，得到：

其KT条件为：

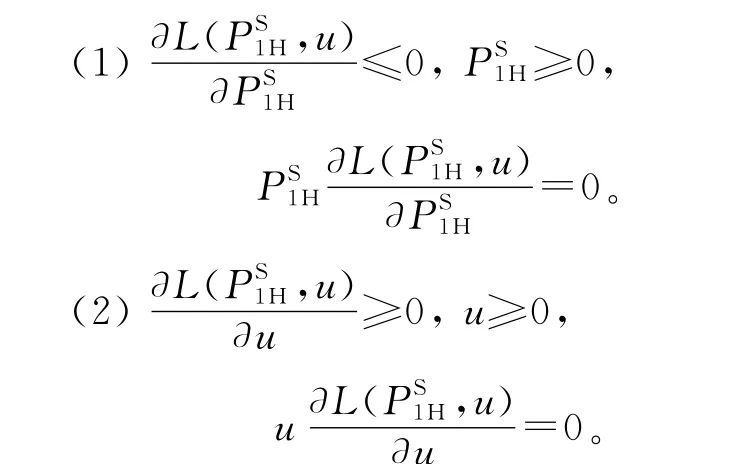
对于u＝0，∂L（PS1H，u）/u≥0（即无约束下的极值点），得到：

对于u＞0，得到：

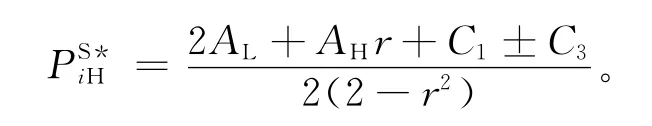
此时∀∈（，）都无法满足约束（31）式。因此，为了与信念（24）式一致，高需求主导零售商应制定价格才能实现分离均衡。

3 算例分析

为了说明本文的相关结论，做进一步的探讨，给出如下算例。假设模型的参数AH＝600，其概率p＝0.3，AL＝400，平均需求μ＝460，替代系数r＝0.5，批发价格w＝50。市场需求差异程度θ＝1.21，小于（2＋r）/（2－r）＝1.67。代入数据得［4（1－p）＋r2（r＋2p－3）］θ＝2.81，大 于（4－2r2）（1－p）＝2.45，由命题1，此时供应商一定会泄露信息。由于θ＜（2＋r）/（2－r），此时市场需求差异程度较小，由命题2的结论，不能形成自然的分离，从而高需求的主导零售商需制定更高的价格以维持分离均衡。比较供应链各方在不泄露信息和泄露信息下的分离均衡定价和收益，结果见表1所列。

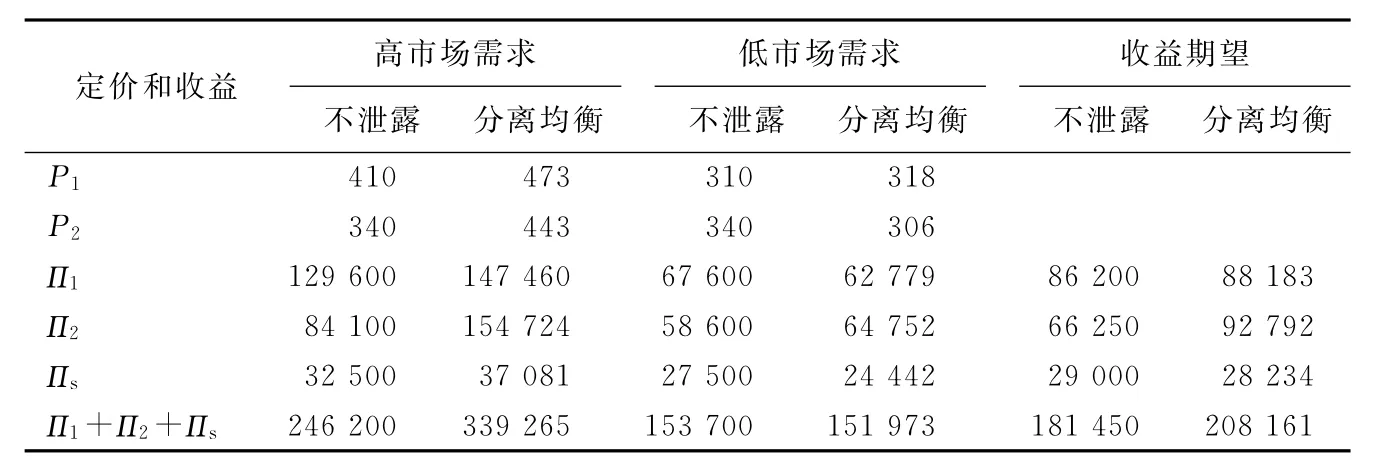
表1 供应链各方的定价和收益

由表1可知，在高市场需求下，供应商泄露信息时的收益37 081比不泄露32 500时多，这与命题1相符，而低市场需求时正好相反。然而供应商泄露信息时的收益期望却比不泄露信息时要少，说明供应商泄露信息时，在高市场需求下增加的收益不能弥补低市场需求下因泄露信息造成的损失。跟随零售商在分离均衡下的收益则明显比不泄露信息下要高，特别是高市场需求下的增幅（由84 100增至154 724）为84%，十分显著。这说明知晓真实的市场需求信息对跟随零售商是十分重要的。

出乎意料的是，主导零售商在信息泄露下的收益期望88 183要比86 200高，说明在高市场需求下，信息泄露使得跟随零售商的定价提高，自身也从中获益，其收益的增加弥补了低市场需求下信息泄露造成的损失。而供应链整体收益也是信息泄露下较高，这些结果与文献［1，3］在研究古诺竞争下的情形是不同的，在伯川德竞争下泄露信息反而能使得主导零售商的收益增加。

4 结束语

本文探讨了伯川德竞争下，供应链由于信息共享所面临的信息泄露的问题。考虑了包含1个供应商和2个进行价格竞争的零售商的供应链，其中主导零售商拥有市场需求的私有信息。通过分析供应商的决策，当满足一定条件时，供应商总会泄露信息。在分离均衡下，尽管信息泄露会造成零售商定价偏离最优，但与不泄露信息时相比，泄露信息反而能使主导零售商以及整个供应链的收益提高。这与先前文献［1，3］在研究古诺竞争下的情形是不同的。这是由于零售商在高市场需求下因信息泄露引起收益的增加，超过了低市场需求下因信息泄露造成的损失。进而，可以得出一个推论：伯川德竞争能降低信息泄露带来的负面作用，更鼓励信息的横向共享。

本文假设2个零售商各自所面临的市场份额是相同的，这存在一定的局限性。对于接下来的研究方向，可以考虑2个零售商之间的市场份额不同的情形。对于混同均衡的情形，由于在混同均衡下供应链的信息结构与不泄露信息下是一致的，故没有对混同均衡做进一步探讨，今后可对混同均衡的情形进行补充。

［1］Kong G，Rajagopalan S，Zhang H.Revenue sharing and information leakage in a supply chain［J］.Management Science，2013，59（3）：556－572.

［2］Hays C L.What Wal－Mart knows about customers’habits［N］.The New York Times，2004－11－14.

［3］Anand K S，Goyal M.Strategic information management under leakage in a supply chain［J］.Management Science，2009，55（3）：438－452.

［4］Lee H L，Whang S.Information sharing in a supply chain［J］.International Journal of Manufacturing Technology and Management，2000，1（1）：79－93.

［5］Chen F.Information sharing and supply chain coordination［J］.Handbooks in Operations Research and Management Science，2003，11：341－421.

［6］¨Ozer¨O，Wei W.Strategic commitments for an optimal capacity decision under asymmetric forecast information［J］.Management Science，2006，52（8）：1238－1257.

［7］经怀明，刘 林，刘心报.两阶段供应链中库存信息共享的价值测算及模拟分析［J］.合肥工业大学学报：自然科学版，2005，28（8）：854－858.

［8］Li L.Information sharing in a supply chain with horizontal competition［J］.Management Science，2002，48（9）：1196－1212.

［9］Zhang H.Vertical information exchange in a supply chain with duopoly retailers［J］.Production and Operations Management，2002，11（4）：531－546.

［10］Li L，Zhang H.Confidentiality and information sharing in supply chain coordination［J］. Management Science，2008，54（8）：1467－1481.

［11］张志清，董绍辉，西 宝，等.需求信息泄露条件下供应链零售商订货策略研究［J］.运筹与管理，2010（1）：80－88.

［12］Xiao T，Qi X.Price competition，cost and demand disruptions and coordination of a supply chain with one manufacturer and two competing retailers［J］.Omega，2008，36（5）：741－753.