一类求解变系数扩散方程的交替分段显－隐式差分方法

刘冬兵，马亮亮

（攀枝花学院 数学与计算机学院，四川 攀枝花 617000）

1 问题的提出

本文的目的是研究适合在并行机与向量机上求解下述变系数扩散方程的有限差分方法，求满足（1）式的解u（x，t）适合初始条件（2）式及边界条件（3）式。

其中，f（x）、g1（t）、g2（t）均为已知的光滑函数；ε（x）为［0，L］上的严格单调递减有界函数，且满足0＜ε0≤ε（x）≤ε1＜＋∞。

在求解上述问题的有限差分方法中，显式方法适合于并行计算，但由于稳定性条件的限制，必须采用非常小的时间步长进行计算，而隐式格式和Crank－Nicholson格式一般是无条件稳定的，但在每一时间层上需要求解线性代数方程组，实现并行计算有一定困难［1－2］。文献［3－6］为解决显式和隐式方法的不足，巧妙地利用Saul’yev非对称格式，设计出了求解一维扩散问题的交替分组显式（AGE）方法，并证明了格式是绝对稳定的，其后又将该方法推广到求解对流扩散方程和二维扩散方程问题；文献［1，7－12］提出了利用Saul’yev非对称格式构造出分段隐式的思想，并且恰当地使用交替技术建立了多种显－隐式和纯隐式交替并行方法；文献［13］将局部一维方法和一维交替分段方法相结合构造出了解二维扩散问题的交替分段显－隐式方法（LASE－I）；文献［14］利用第二类Saul’yev非对称格式给出了一类求解扩散方程的交替分组显式格式；文献［15］尝试将空间分数阶扩散方程交替方向有限差分法实现基于消息传递接口（Message Passing Interface，MPI）的并行化计算；文献［16－17］采用交替方向隐式欧拉方法对偏积分微分方程进行了数值求解；文献［18］对高维抛物型方程构造了一个高精度恒稳定的交替方向格式；文献［19］对三维抛物型方程构造了一个高精度恒稳定的紧交替方向差分格式；文献［20］对于非线性电报方程的初边值问题，用交替方向有限差分法和交替方向有限元法2种方法构造计算格式，并且进行理论分析。本文将应用交替分段显－隐式差分方法进一步考虑变系数扩散方程（1）式的求解问题。

2 变系数交替分段显－隐式差分方法

首先对求解区域（0，L）×（0，T）进行网格剖分，在网格点（xi，tn）上计算（1）式的解u（xi，tn）的近似值。设h和τ分别为空间步长和时间步长，选取正整数M和N，并令h＝L/M，τ＝T/N。记xi＝ih，i＝0，1，…，M；tn＝nτ，n＝0，1，…，N。空间步长h＝xi＋1－xi，i＝0，1，…，M－1；时间步长τ＝tn＋1－tn，n＝0，1，…，N－1；平行坐标轴平面：x＝xi＝ih，t＝tn＝nτ（i＝0，1，…，M－1；n＝0，1，2，…，N－1）；网格节点为（xi，tn）。易知网格包含（M－1）个内点，为方便起见，记r＝τ/h2。

在构造变系数交替分段显－隐式差分方法时，需要用到方程（1）式的古典显式差分格式，即

隐式差分格式，即

Saul’yev非对称差分格式［21］，即

如果第n时间层的近似解已知，则利用（6）式通过自左至右的递推可计算求得第n＋1层的近似解。类似地，在n层计算第n＋1层时可利用（7）式通过自右向左进行显式递推计算。

下面描述适合于并行计算的变系数交替分段显－隐式差分方法，其基本思想是：在n＋1时间层把x轴上N－1个点均分成nx段，每段含l个点，要求l≥3，nx≥3，且nx是奇数。在奇数时间层上按“古典显式－分段隐式－古典显式”规律进行计算，在偶数时间层上按“分段隐式－古典显式－分段隐式”规律进行计算，使得“古典显式”与“分段隐式”在不同时间层上交替进行。具体做法如下：设N－1＝lk，l，k＝nx均为正整数，且l，k≥3，k为奇数，N－1个内点可分别按奇数时间层和偶数时间层进行点数稍有不同的分段。在奇数时间层tn＋1上，把N－1个内点分成k段，每段包括l个内部节点。为构造交替分段显－隐式差分方法，先引入分段隐式格式。对于第m（1≤m≤k）段，设其节点为（xim＋p，tn＋1），p＝1，2，…，l，在此段的左端 点（xim＋1，tn＋1）上 采 用（6）式，在右端点（xim＋l，tn＋1）上采用（7）式，而在此段其余节点上使用（5）式。

因此，在第k段上的计算格式可以写成如下矩阵形式的差分方程组：

对于已经分好的k段，当m（1≤m≤k）为奇数时采用分段隐式格式（8）式；当m（1≤m≤k）为偶数时采用古典显式格式（4）式。第1段和第k段均用分段隐式格式，但第1段左端点（x1，tn＋1）处和第k段右端点（xN－1，tn＋1）处则使用隐式格式（5）式。在偶数时间层tn＋1上，分段情况与奇数时间层稍有差别，总段数仍为k段，但每段所含节点数有所变化，奇数段含有l－2个节点，偶数段含有l＋2个节点，第1段和第k段各含有l－1个节点，内部节点总数仍为lk个。在奇数段上采用（4）式，在偶数段上采用（8）式。

3 方法的稳定性

下面给出变系数交替分段显－隐式差分方法矩阵形式的数学描述。令

Op为p×p阶零矩阵。记

则由（8）式给出的变系数交替分段显－隐式差分方法可以表示为：

其中，I为 单位矩阵；b1＝（，0，…，0）T；b2＝，0，…，0）T；G1、G2为由k个子矩阵组成的（N－1）×（N－1）阶块对角矩阵。

引理1由（9）式和（10）式表示的矩阵G1、G2均为非负实矩阵，即G1＋（G1）T、G2＋G2T非负（或正）定［22］。

引理2如果ρ＞0，矩阵G为非负矩阵［5］，则

定理1求解变系数扩散问题（1）～（3）式的交替分段显－隐式差分方法（11）式、（12）式是无条件稳定的。

证明由（11）式和（12）式得：

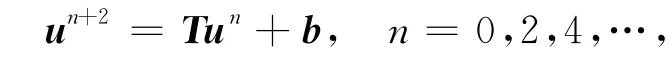
其中，T＝（I＋rG2）－1（I－rG1）（I＋rG1）－1（I－rG2）；b＝（I＋rG2）－1［（I－rG1）（I＋rG1）－1b1＋b2］。

利用引理2，可得：

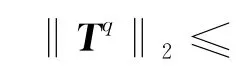
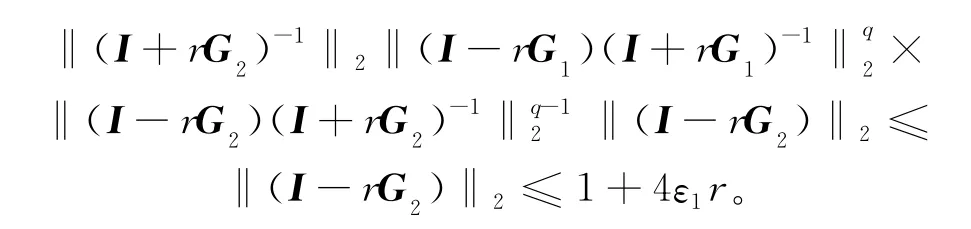
于是，对于任何正整数q，有‖Tq‖2≤C，C＝1＋4ε1r，可见，变系数交替分段显－隐式差分方法（11）式、（12）式是绝对稳定的。

4 截断误差分析

定理2当l＝3，k＝5时，变系数交替分段显－隐式差分方法（11）式、（12）式的截断误差分别为［2］：

证明根据题意，N－1＝lk＝15，由（11）式可得：

类似可得到i＝10，11，12对应的表达式。

下面分3种情况讨论变系数交替分段显－隐式差分方法（11）式和（12）式的截断误差，从而证明定理2的正确性。

（1）情形1。由（12）式、（13）式可得：

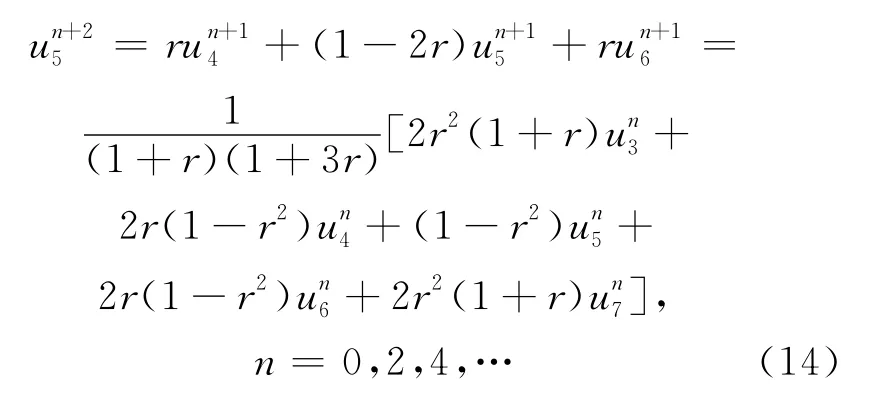
分别将（14）式中的和（i＝3，4，5，6，7）在点（5，n＋1）处作泰勒展开，可得：

因此，（14）式的截断误差为O（τ＋h2），和（14）式有相同结构的表达式，故其截断误差也为O（τ＋h2）。

（2）情形2。根据（12）式、（13）式有：

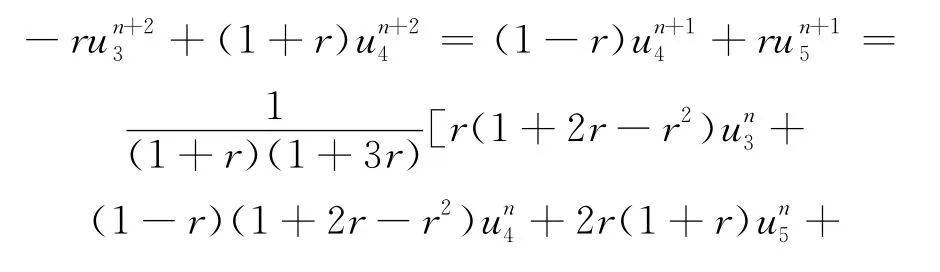
分别将（15）式、（16）式中的（i＝3，4）、（i＝3，4，5，6，7）和（i＝6，7）（i＝3，4，5，6，7）在（4，n＋1）、（6，n＋1）2点处作泰勒展开，可得：

其中，α＋β＝5。注意到（17）式、（18）式中的若干项系数只差一个符号，可以在相应的项之间抵消部分误差，从而增加逼近精度。事实上有：

其中，0＜θi＜2（i＝1，2，3）。

由此可得（17）式、（18）式的截断误差为O（τ＋h2）。类似地，可列出左端分别为－＋（1＋r）和－＋（1＋r）的2个方程式，它们具有和（17）式、（18）式相同的截断误差。

（3）情形3。根据（11）式、（12）式易得到：

其中，i＝1，2，3，7，8，9，13，14，15。（22）式具有O（τ2＋h2）的截断误差。

5 数值例子

考虑下面的例子：

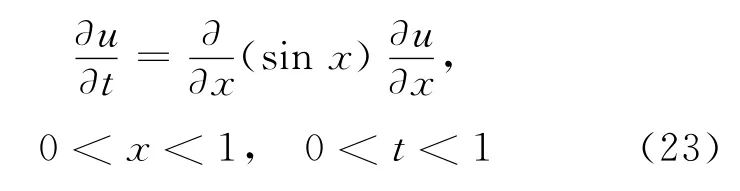
初始条件和边界条件为：

方程（23）～（25）式的精确解为：

取定时间步长τ＝0.000 1和空间步长h＝0.025。图1所示为t＝0.01时刻由变系数交替分段显－隐式差分格式（11）式、（12）式计算得到的数值解与方程精确解的平面图，可以看出数值解收敛于方程的精确解。图2所示为差分格式（11）式、（12）式计算得到的数值解与空间轴、时间轴之间的三维立体图。表1所列为用逼近格式（11）式、（12）式求得的数值解与精确解的比较，可以看出数值解与精确解较为吻合。

图1 数值解与精确解比较

图2 三维立体图

表1 当t＝0.01，h＝0.025，τ＝0.000 1时的精确解、数值解及误差

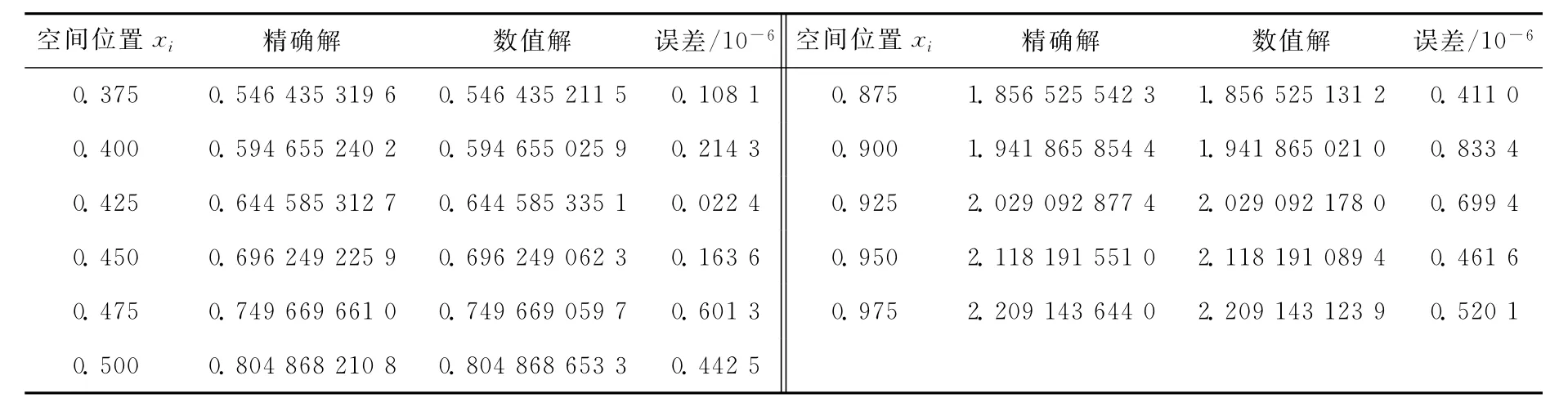
续表

6 结束语

本文以一维变系数扩散方程为模型，给出了一种求解其数值逼近问题的交替分段显-隐式差分格式（11）式、（12）式。最后，用数值例子验证了文中构造的变系数交替分段显－隐式差分格式（11）式、（12）式的有效性，结果显示该方法具有很好的并行性且无条件稳定。

［1］张宝琳.求解扩散方程的交替分段显－隐式方法［J］.数值计算与计算机应用，1991，12（4）：245－253.

［2］陆金甫，张宝琳，徐 涛.求解对流－扩散方程的交替分段显－隐式方法［J］.数值计算与计算机应用［J］.1998，19（3）：161－167.

［3］Evanas D J，Abdullah A R.Group explicit methods for parabolic equation［J］.Int J Comput Math，1983，14：73－105.

［4］Evanas D J，Abdullah A R.Alternating group explicit methods for the diffusion equations［J］.Applied Math Modelling，1985，9：201－206.

［5］Evanas D J，Abdullah A R.A new explicit method for the diffusion－convection equation［J］.Computers ＆ Mathernatics with Applications，1985，11：145－154.

［7］Zhang Baolin，Xu Xiumin.Alternating block explicit－implicit method for the two－dimensional diffusion equation［J］.Int J Comput Math，1991，38：241－255.

［8］Zhang Baolin.Alternating segment explicit implicit method for the diffusion equation［J］.J Num Method ＆ Comp Appl，1991，12：245－253.

［9］Chen Jin，Zhang Baolin.A class of alternating block Crank－Nicolson method ［J］.Int J Comput Math，1992，45：89－112.

［10］张宝琳，袁国兴，刘兴平，等.偏微分方程并行有限差分方法［M］.北京：科学出版社，1994：220－234.

［11］Zhang Baolin，Su Xiumin.Alternating segment Crank－Nicolson scheme［J］.计算物理，1995（1）：115－120.

［12］Zhang Baolin，Li Wenzhi.On alternating segment Crank－Nicolson scheme ［J］.Parallel Computing，1994，20：897－902.

［13］刘晓遇，黄 涛.求解二维扩散方程的交替分段显－隐方法［J］.清华大学学报：自然科学版，1996，36（2）：22－28.

［14］王文洽.求解扩散方程的一类交替分组显式方法［J］.山东大学学报：理学版，2002，37（3）：194－199.

［15］李晓.分数阶扩散方程交替方向并行算法［D］.山东大学，2014.

［16］黎丽梅.交替方向隐式欧拉方法在偏积分微分方程中的应用［J］.北华大学学报：自然科学版，2012，13（2）：149－152.

［17］黎丽梅.交替方向隐式差分法在分数次微分方程中的应用［J］.湖南理工学院学报：自然科学版，2012，25（3）：11－13.

［18］张星，单双荣.高维抛物型方程的一个高精度恒稳定的交替方向格式［J］.工程数学学报，2011，28（1）：61－66.

［19］陈贞忠，马小霞.三维抛物型方程的紧交替方向差分格式［J］.河南科技大学学报，2011，32（3）：79－85.

［20］杨贵香.求解电报方程的两种交替方向法［D］.新乡：河南师范大学，2014.

［21］Saul’yev V K.Integration of equations of parabolic type by method of nets［M］.New York，1964.

［22］张志跃.变系数对流扩散方程的交替分段显－隐方法［J］.山东大学学报：理学版，2002，37（2）：120－123.