基于自回归分布滞后模型的地面沉降预测

2015-03-29郇小龙甄宗坤

测绘工程 2015年9期

郇小龙，甄宗坤

（1．上海市建工设计研究院有限公司，上海200050；2．苏州工业园区测绘地理信息有限公司，江苏苏州215000）

地面沉降是一个复杂的、多种因素共同作用的环境地质现象，严重时表现为地质灾害，引起地面沉降的主要因素可分为人为因素和自然因素［1－3］。目前对地面沉降的研究工作主要围绕人为因素展开，其中过量抽取地下水引起地面沉降成为最主要的研究对象［4－9］。

经大量研究表明，地下水水位的变化对地面沉降的影响是一个长期的过程，它往往会持续几个监测时期，在这一过程存在时间滞后，地下水水位的变化需要经过一段时间才能导致地面沉降。另一方面，地面沉降以前的变化趋势以及变化规律会延续到本期，从而使得地面当前沉降量受到自身过去沉降量的影响［10－12］，因此，针对地面沉降与地下水水位变化不同步，并考虑到地面下沉受到自身的影响，本文建立考虑滞后作用的地面沉降自回归分布滞后预测模型。

1 模型的建立与估计

1．1 自回归分布滞后模型的建立

一般来说，地面沉降量与地下水水位变化幅度呈高度正相关，而且地面沉降的产生和发展过程与地下水的开采过程往往滞后一个时段，在这个过程中，会出现地下水水位的现值决定地面沉降量预期值的情况，也就是说本期的地下水水位直接决定了地面将来的沉降量［13－15］，即两者之间存在关系：

式中：S＊t为地面沉降量的预测最佳值，Ht－1为地下水水位的现值，μt为随机误差项，α为常量，β为模型参数。

然而，地面沉降的发展受到其他因素的影响，地面沉降在短时间内不会完全达到预测值预测值与实测值存在一定误差，两者之间的关系：

式中：St为当期实测值，St－1为前一期实测值，λ为调整系数，St－St－1为地面沉降实际变化量，－St－1为地面沉降最优预测变化量。

式（2）表示由于存在滞后作用，地面沉降实际变化量与地面沉降最优预测变化量的一个比值，即调整系数λ，表明地面沉降预测值需要调整一段时间才能达到实测值的水平。一般情况下，0＜λ＜1，它代表调整到实测值水平的速度，λ越大，表示调整速度越快。假如λ＝0，由式（2）可知St＝St－1，表示地面当期和前一期沉降量一样，完全没有调整；假如λ＝1，则有＝St，表示地面沉降预测最佳值等于实测值，当期完全实现调整。

整理式（2）模型变为

从式（3）可知地面沉降的实测值St是地面沉降预测最佳值与前一期地面沉降实测值St－1的加权和，加权数分别为λ和1－λ。

将式（1）代入式（3），并整理各项，得到转换形式：

令

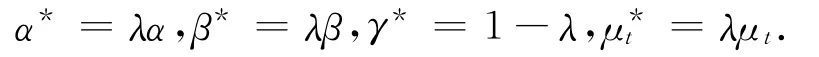
则模型变为

该模型就是自回归分布滞后模型，如能得到该模型的参数估计，代入式（5）得到地面沉降量与地下水位以及本身的模型关系表达式。

1．2 模型参数估计

对于自回归分布滞后模型St＝α＊＋β＊Ht－1＋γ＊St－1＋，其中，＝λμt。普通最小二乘的估计要求自变量Ht－1，St－1与随机误差项μt相互独立，此外，随机误差项μ＊t不能存在自相关，否则会导致最小二乘是有偏的和非一致的估计。因此，在对模型进行最小二乘估计前必须考察μ＊t之间是否存在自相关以及自变量Ht－1，St－1与μ＊t是否相互独立。

假设模型St＝λα＋λβHt－1＋（1－λ）St－1＋λμt随机误差项μt满足古典假定：

1）零均值假定：随机误差项μt的数学期望为0，即E（μt）＝0；

2）同方差假定：随机误差项μt有相同的方差，即Var（μt）＝E（）＝σ2；

3无自相关性假定随机误差项μi和μj的协方差为0，即Cov（μi，μj）＝0（i≠j）；

4）自变量Ht－1，St－1与随机误差项μt不相关，即Cov（Ht－1，μt）＝Cov（St－1，μt）＝0。

根据以上假定则有

由此可知，随机误差项μ＊t不存在自相关，自变量Ht－1，St－1与μ＊t不相关，因此可以直接采用最小二乘法对模型参数进行估计。

根据最小二乘法准则，则有

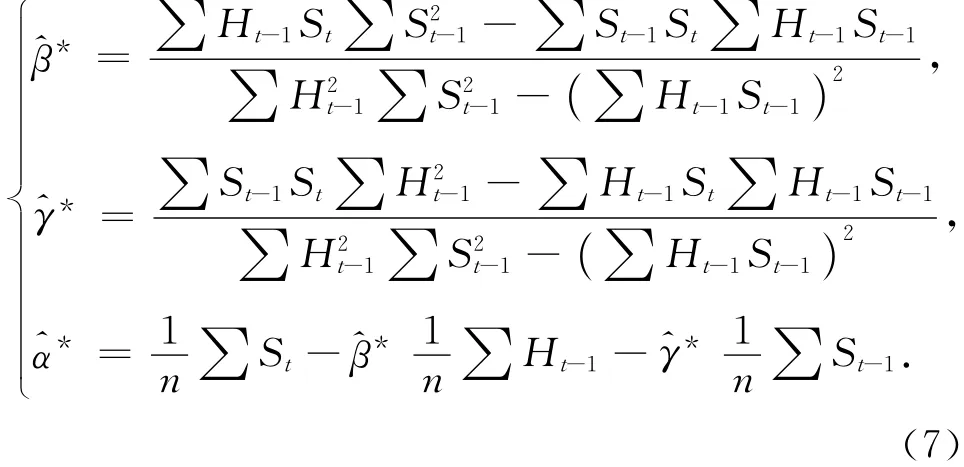
2 实例计算及模型评价

2．1 实例计算

现收集到某地区1978年～2000年连续23年内的地下水水位以及地面沉降量数据，如图1所示，采用前文所述的自回归分布滞后模型探讨地面沉降量与地下水位以及本身的关系。

图1 某地区地下水水位以及地面沉降量数据

分别用S和H两个序列来表示地面沉降量和地下水水位数据，对S和H两时间序列建立自回归分布滞后模型，采用最小二乘法对模型参数进行估计，预测模型：

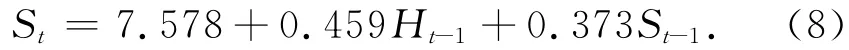
式中：St为第t年的地面沉降量，Ht－1为第t－1年的地下水水位，St－1为第t－1年的地面沉降量。

2．2 模型评价

预测模型决定系数R2＝0．986 82，表明总离差平方和的98．682%被预测模型解释，只有1．318%未被解释，因此预测模型对实测值的拟合优度较高，说明预测模型拟合效果较好，图2为模型预测值与实测值的对比。

图2 模型预测值与实测值的对比

对自回归分布滞后模型做预测分析，分析结果如表1所示，计量学中规定若平均绝对百分误差（MAPE）取值在0～5之间，则预测精度较高，本文自回归分布滞后模型的平均绝对百分误差MAPE＝2．954，说明模型预测效果较理想。希尔不等式系数（TIC）介于0～1之间，且数值越小预测精度越高，本模型TIC＝0．014，进一步说明模型预测效果较好。

表1 模型预测分析结果

3 结束语

针对地面沉降与地下水水位变化不同步，并考虑到地面下沉受到自身变化趋势的影响，本文建立考虑滞后作用的地面沉降自回归预测模型，以收集到的某地区地面沉降数据为例进行计算，探讨模型拟合效果与预测精度。结果表明，自回归分布滞后模型对实测值的拟合优度较高，模型拟合效果较好，此外，模型平均绝对百分误差和希尔不等式系数满足要求且较小，预测精度较高。因此，自回归分布滞后模型可以推广到预测地面沉降领域中去。

［1］徐光黎，佟永贺，张家明．地下水抽汲对西安地面沉降和地裂缝活动的影响程度分析［J］．中国地质灾害与防治学报，1992（4）：3－7，15．

［2］王伟．抽取地下水引起的地面沉降可视化研究［D］．南京：河海大学，2006．

［3］何伟，李明，阚起源．抗差加权非等时距GM（1，1）模型在大型建筑物沉降预测中的应用［J］．测绘工程，2014，23（4）：62－64，68．

［4］孙泽信，庞逸群，黄腾．改进的灰色模型在建筑物沉降预测中的应用［J］．测绘工程，2010，19（3）：59－62．

［5］周吕，文鸿雁，韩亚坤．灰色预测与Kal man滤波在建筑物沉降变形分析中的应用［J］．测绘科学，2014，39（4）：149－151．

［6］程晨．灰色理论和多项式拟合在地表沉降监测中的应用［J］．测绘与空间地理信息，2014，37（2）：220－222．

［7］刘丹丹．灰色模型分析法在高层建筑物变形监测预测中的应用［J］．测绘与空间地理信息，2014，37（2）：203－205．

［8］王静，唐仲华，邓青军，等．地下水开采导致总应力变化对地面沉降的影响［J］．工程勘察，2012（5）：34－37．

［9］肖功衍，储征伟．浅表地下水水位变化对地面沉降的影响［J］．城市勘测，2007（4）：52－53，86．

［10］薛禹群，张云，叶淑君，等．中国地面沉降及其需要解决的几个问题［J］．第四纪研究，2003（6）：585－593．

［11］曹昶，樊重俊．非等间距无偏GM（1，1）模型在建筑沉降预测中的应用［J］．测绘工程，2013，23（6）：55－57．

［12］王彩会，陈杰，朱锦旗．开采浅层地下水对地面沉降影响的探讨［J］．中国地质灾害与防治学报，2004（4）：82－84．