参数有界约束下的最小二乘平差算法

左廷英，陈仲儿，宋迎春

（中南大学 地球科学与信息物理学院，湖南 长沙410083）

在测量平差中，通常以G－M模型为平差模型，同时顾及非线性模型线性化的误差［1－2］，求得的简化模型往往是不准确的，因而参数估值也非其准确值，即参数存在不确定性［3－4］。尤其是在一些特殊情况下（如高精度GPS变形监测网），由于模型给的不准、观测误差、参数的不确定性等不确定性因素的影响，从而使得参数的最小二乘估值可能是与实际相违背的，即最小二乘的平滑、去噪性掩盖了形变的真实信息，其原因在于没有考虑系统的物理特性或先验信息，运用纯数学方法来处理，导致估值“失真”。

在参数估计问题上，整体最小二乘法是对以上不确定性的一个改进。其将系统中不确定因素扩展到了模型问题上，综合考虑设计矩阵与观测噪声误差，估计得到的参数值在某些场合下［5－7］优于最小二乘解。

整体最小二乘参数估计方法存在不足，其最大限制因素是必须了解观测信息的统计特性和隶属函数，而由于不确定性因素的出现，往往较难获得上述统计信息。最小二乘法、整体最小二乘法都是通过人为的手段对其确定，这样显然是不合适的。相反，较之统计特性，获取参数的上下界、误差的极限值等［8］相对较容易些。国内外学者对此类问题也做探讨和研究 并成功摸索出一条求解上述不确定问题的道路［9－11］。就目前研究情况而言，较为成熟的解决办法是区间分析，其已在岩土力学、结构力学等地质、材料方面取得了一些成绩［9－11］。但由于区间分析的缺点和不足，多数学者更多关注的是其理论研究［12－13］。在测绘领域方面，陶本藻、王新洲和杨元喜等都对测量不确定度理论进行研究，拓展了测量平差数据处理的理论和方法。本文基于参数有界性，构建了参数有界约束下的平差模型，利用最小二乘原理，将问题转化为附有箱型约束的二次规划问题，运用最优化理论知识［14－15］来处理，进而得到参数的一个可行解，并将其应用到沉降监测网实例中，得出较为合理的结果。

1 参数有界约束下的最小二乘平差算法

1．1 建立平差模型

参数有界约束下的平差模型：

其中，B是一个n×t的设计矩阵；X＝［x1…xt］Τ是t×1的参数向量；Δ是随机误差向量，Δ～N（0，σ2I），I是单位矩阵；c＝［c1…ct］Τ，d＝［d1…dt］Τ分别为参数的上、下界。

1．2 转化为附有箱型约束的二次规划问题

式（1）的解不只一组，故需附加最小二乘约束来求得参数的最优解。

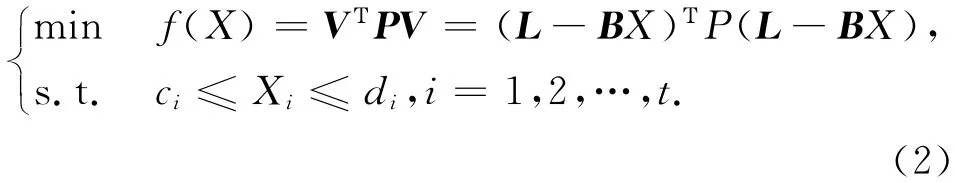
从而转化为附有箱型约束的二次规划问题：

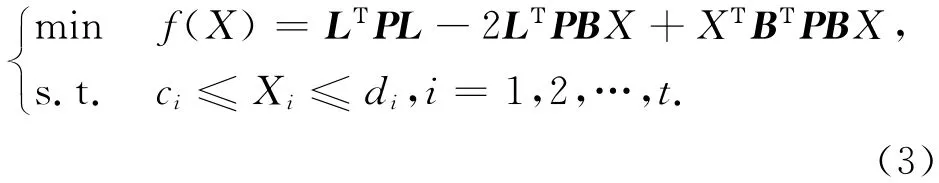
当网中各观测量为等权观测量时，上式转化为

其中，BΤPB是一个对称正定（半正定）矩阵，式（3）中可简化为

上式是一个凸函数。其中，N＝BΤPB，W＝BΤPL。故式（3）可等价为一个凸二次规划问题：

其中，F（X）＝f（X）－LΤPL。

1．3 由分解算法计算参数估值

求解上述凸二次规划问题的算法有很多，如内点算法、积极集法、对偶方法等［16－18］，需要具有深厚的最优化理论及数学知识，且没有一个通用、简单的算法来实现。本文采用文献［19］中提到的一种分解算法来处理，以下称“分解算法”。具体内容如下：

N∈Rt×t是对称矩阵，且N满足下述条件：

N＝N1＋N2；N1－N2是对称正定矩阵，其中N1，N2∈Rt×t。

则称（N1，N2）为N的一正则分裂。

设＾X为问题（1）的最优解，显然有X＝＾X＋（X－＾X），因此

故而转化为等价问题：

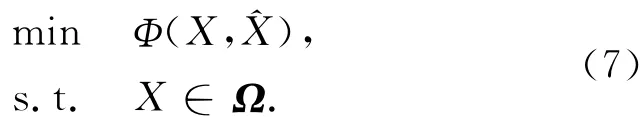
其中，Ω是式（3）的解集。

箱型约束二次规划问题的分解算法：

2 算例与分析

图1所示为南方某城市工业区部分沉降监测网略图，由于工业需要，大量开采地下水造成较为严重的地面下沉，为避免安全事故及不必要的人员和财产损失，在近几年已响应相关部门要求，禁止了地下水的过度开采 同时采用二等水准测量方法获得了前后两期高差观测值，其中BM1点为已知点（国家二等水准点），高程为27．329 m，观测周期为1年，观测精度为0．86 mm。表1为两期高差观测成果。通过前后两期水准测量获得的高差观测值来分析地面沉降量。在具体处理过程中，以网中BM1点为固定点，其他点为待定点，由此建立参数有界约束下的平差模型：

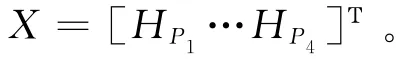
相应的附有箱型约束的凸二次规划问题为

其中，N对称正定，F（X）为严格凸函数。

图1 沉降监测网

表1 两期高差观测成果

解决上述问题关键在于如何确定参数（高程）的上下界，即上述模型中的c，d值。经过对Ⅰ期水准网做经典自由网平差处理 可以得到参数的最或然值，在做Ⅱ期平差处理时，以Ⅰ期平差得到的参数值作为本次平差参数初值。根据已有资料显示，在过去几年，该地区年沉降量最大值不超过10 mm，由变形机理可知，由于禁止令的实施，其沉降量不应超过往年最大值，故可近似认为前后两期沉降量不超过一个10 mm，如此就确定了参数的上下界。即

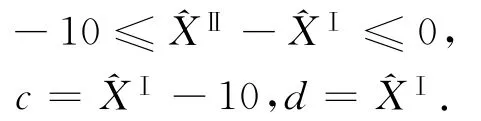
为了比较传统最小二乘平差法与参数有界约束下的最小二乘平差算法的优劣性，在具体处理过程中，本文还对前后两期水准网做了经典自由网平差处理。同时为便于描述，分别将经典自由网平差法和参数有界约束下的最小二乘平差算法记为LS、BLS。经过MATLAB编程实现，两种方法求得的参数估值及沉降量如表2、表3所示。

表2 两种方法的参数估计结果 mm

表3 两种方法得到的沉降量 mm

由上述结果可见，当限定前后两期网中待定点沉降量不超过10 mm时，由经典自由网平差得到的参数估值已明显不能满足该要求，如P4点的沉降量已超出约束界限。而在同一个水准网中，各待定点沉降量应该相差不大，故参数有界约束下的最小二乘平差算法得到的结果较符合真实情况。

3 结束语

经典最小二乘平差法基于传统高斯—马尔科夫模型 具有诸多优良特性 可以得到参数的最优估值，但由于不确定性问题的出现，依靠其单一平滑去噪的特点已然不能满足高精度变形监测数据处理要求，因此亟待构建一个与真实系统更为接近的模型并提出相应算法，较为有效的解决办法是利用已知的先验信息或通过其他相关途径，对模型附加约束条件，如参数有界，建立参数有界约束下的平差模型，并运用相关知识来求解。实践证明，经过最优化处理，得到的模型全局最优点为参数的最佳估值，且满足在参数有界下残差平方和最小的原则，得到的估计结果在某些情况下可能比最小二乘更能反映系统真实状态。对于小型变形监测网数据处理较为适用。

本文以某一沉降监测网为算例，分别采用经典最小二乘法和基于参数有界约束下的最小二乘平差算法来处理，新算法的估值更符合实际。但在实际工作中，往往无法获知系统的先验信息，因此如何更为有效确定参数初值及上下界还有待深入研究。事实上，多数情况下的变形监测网为GPS变形监测网，此时参数为三维且方程维数较大，对于该类问题，需进一步延伸。同时，分解算法虽简单实用，但在具体执行时，效率不高，需迭代多次才接近收敛，故迫切需要提出一种新的最优化算法来解决参数有界问题。

［1］ 王新洲．非线性模型能否线性化的实用判据［J］．武汉测绘科技大学学报，1999，24（2）：145－148．

［2］ 张朝玉，陶本藻．平差系统的模型误差及其识别方法研究［J］．武汉大学学报：信息科学版，2005，30（10）：897－899．

［3］ CHANDRASEKARAN S，GOLUB C H，GU M，et al．Parameter Esti mation in the Presence of Bounded Data Uncertainties［J］．SIA M Jour nal on Matrix Analysis and Application，1998，19（1）：235－252．

［4］ CHANDRASEKARAN S，GOLUB C H，GU M，et al．Parameter Estimation in the Presence of Bounded Mod－eling Errors J．IEEE Signal Pr ocessing Letters 1997 4（7）：195－197．

［5］ 丁克良．整体最小二乘法及其在测量数据处理中的若干应用研究［D］．武汉：中国科学院测量与地球物理研究所，2006．

［6］ 楚彬，范东明．基于比例整体最小二乘的GPS高程拟合［J］．测绘工程，2014，23（4）：37－39．

［7］ 袁豹，岳东杰，张亮，等．基于总体最小二乘的相似变换模型及其在地图扫描数字化中的应用［J］．测绘工程，2013，22（4）：45－47．

［8］ 刘世君，徐卫亚，王红春．不确定性岩石力学参数的区间反分析［J］．岩石力学与工程学报，2004，23（6）：885－888．

［9］ 罗麟．区间分析法在滑坡灾害风险评价中的应用研究［D］．北京：中国地质大学，2008．

［10］邱天．区间分析在边坡工程中的应用［D］．南京：河海大学，2006．

［11］于生飞．基于区间不确定方法的边坡稳定性分析及非概率可靠度评价研究［D］．南京：南京大学，2012．

［12］邱志平，顾元宪．有界不确定参数结构位移范围的区间摄动法［J］．应用力学学报，1999，16（1）：1－9．

［13］苏静波．工程结构不确定性区间分析方法及其应用研究［D］．南京：河海大学，2006．

［14］袁亚湘，孙文瑜．最优化理论与方法［M］．北京：科学出版社，1997：422－451．

［15］寇述舜．凸分析与凸二次规划［M］．天津：天津大学出版社，1994：148－182．

［16］张艺．框式约束凸二次规划问题的内点算法［J］．高等学校计算数学学报，2002（2）：163－168．

［17］COLEMAN T F，LAURIE A H．A Direct Active Set Algorith m f or Lar ge Sparse Quadratic Programs with Simple Bound［J］．Mathematical Programming，1989，45：373－406．

［18］马圣容．杨正豪．一类凸二次规划的对偶方法［J］．南京师大学报：自然科学版，2003，26（1）：39－44．

［19］卢战杰，魏紫銮．边界约束二次规划问题的分解方法［J］．计算数学，1999，21（4）：475－482．