基于最小二乘法的感应电能无线传输系统负载辨识方法

苏玉刚 陈 龙 王智慧 呼爱国 戴 欣

(1.重庆大学自动化学院 重庆 400030 2.奥克兰大学电子与计算机工程系 奥克兰 1010)



基于最小二乘法的感应电能无线传输系统负载辨识方法

苏玉刚1陈 龙1王智慧1呼爱国2戴 欣1

(1.重庆大学自动化学院 重庆 400030 2.奥克兰大学电子与计算机工程系 奥克兰 1010)

基于最小二乘法提出一种新型负载辨识方法，以PS结构电流型感应电能传输(IPT)系统为例，建立其非线性高阶微分方程并构建数据矩阵，通过最小二乘法获得系统的过程参数矢量，将负载辨识问题转换为系统参数辨识问题，完成系统的负载辨识，最后通过仿真及实验，验证了此方法的可行性。

感应电能传输(IPT) 最小二乘法 参数辨识

0 引言

感应电能传输(Inductive Power Transfer，IPT)技术是一种借助时变电磁场将电能从电源端耦合到负载端的电能传输新技术[1，2]。IPT技术理论及其关键技术的深入研究，推动了IPT技术在电动车充电、电子产品充电、生物医电以及照明系统等诸多领域的广泛应用[3-9]。

在某些实际应用中(例如厨房家电)，能量拾取装置按要求放置于能量发射平台上，且发射线圈与拾取线圈之间距离固定，此情况下可将互感近似视为定值，但负载的改变无法避免。由于系统负载的变化，源自能量接收端(二次电路)的反射阻抗会在能量发射端(一次电路)具有相应变化，使得一次电路的固有频率发生漂移[10]，从而不再与工作频率匹配。这将导致系统偏离软开关工作点，从而影响系统的功率传输能力，增加开关损耗及电磁干扰(EMI)[11]。此外，当负载变化，系统需根据当前负载情况调整能量发射端的控制模式，实现系统的最佳效率跟踪控制，负载辨识是其关键问题。因此，为了建立更加高效、可靠、稳定的IPT系统，负载的辨识问题亟待解决。然而，系统的高阶非线性使得负载辨识问题成为一个技术瓶颈。针对上述问题，文献[12-14]基于系统的能量模型，从能量守恒角度建立方程，完成对负载的辨识。文献[15]在初始时刻给系统注入能量，随后使其自由振荡，通过推导出一次电流衰减率与负载之间的关系完成负载辨识，但不是一种稳态下的负载辨识策略。

本文基于最小二乘法提出一种新型的负载辨识策略。以PS结构的电流型IPT系统为例，通过建立系统非线性高阶微分方程完成对数据矩阵的构建，并在此基础上利用最小二乘法完成对系统过程参数的辨识，通过过程参数矢量及负载间的线性关系完成对负载的辨识，将直接对负载辨识的问题转换为对系统参数辨识的问题。最后通过仿真分析及实验验证了此方法的可行性，且具有一定准确度，是一种易实现的负载辨识方法。

1 主电路拓扑

图1给出了较常见的PS结构电流型IPT系统。该系统由一次电路及二次电路两个独立部分所组成。在一次侧部分，直流电压源Edc提供整个系统的电能输入，Ldc为滤波电感，Edc与Ldc串联可近似视为电流源并在稳态时产生近似恒定电流idc。开关管S1～S4构成一次高频逆变电路，两组开关管(S1，S4)及(S2，S3)轮流导通将DC激励电流idc逆变为高频方波电流iac，一次电容Cp、一次绕组Lp构成一次并联谐振电路；在二次侧部分，二次电容Cs、二次绕组Ls构成二次串联谐振电路，二级管VD1～VD4及滤波电容C构成二次整流电路，将高频交流电压转换为电压uo作用于负载RL上。其中，M为耦合电感Lp、Ls之间互感，Rp、Rs分别为电感Lp、Ls串联等效电阻。

对于一次电路，电压源Edc产生直流电压流经滤波电感Ldc，通过高频逆变电路后输出近似方波的电流iac；对于二次电路，带有滤波电容C的整流电路与负载RL并联时可等效为负载Req，等效负载Req的阻抗由

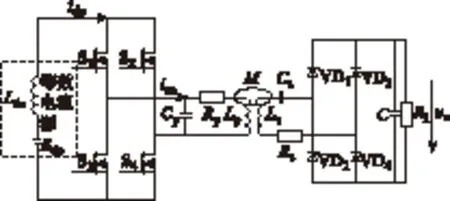
图1 基于PS型IPT系统主电路拓扑Fig.1 The main circuit of a PS-type IPT system

Req=(8/π2)RL≈0.81RL

(1)

因此可得到主电路的等效电路，如图2所示。其中，iac为一次逆变器输出方波电流，up为一次谐振电容Cp端电压，ip为一次绕组谐振电流，us为二次谐振电容Cs端电压，is为二次绕组谐振电流，R1为电阻Req、Rs串联等效电阻，即

R1=Req+Rs

(2)

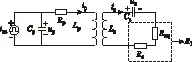
图2 基于PS型IPT系统的等效电路图Fig.2 The equivalent circuit of PS-type IPT system

2 IPT系统负载辨识

2.1 基于最小二乘法的参数辨识

对于上述IPT系统，可获得如下形式的差分方程

z(k)+a1z(k-1)+…+amz(k-m)=

b1u(k)+…+bn+1u(k-n)

(3)

由于k存在一系列取值，因此可进一步将式(3)改写为矩阵形式

ZL=HLθ

(4)

其中

(5)

(6)

(7)

式中，ΗL为系统数据矩阵；L为数据长度。

当负荷功率分别为2 MVA、4 MVA、6 MVA，功率因数为0.85，XC=0时，串补装置处节点电压分别为9.57 kV、8.89 kV、8.19 kV，若加入补偿度k=2.25的补偿电容时，补偿点电压分别提升1.272 kV、1.591 kV、1.668 kV。结果如图4所示：容量与电流的平方成正比，而串联电容器补偿的电压与线路电流成正比。因此，当线路容量增大时，电流增大，补偿的电压也随之增大。这就是串补的负荷自适应特性，也是其他无功补偿均不具备的特性。

显然，可通过最小二乘法，得到过程参数矢量θ的最小二乘估计

(8)

2.2 IPT系统数据矩阵构建及负载辨识

为了获得IPT系统的过程参数矢量及数据矩阵，首先建立系统非线性微分方程。

由图2所示的等效电路图，构建如下方程

(9)

选取一次逆变器输出方波电流iac及一次绕组电流ip作为考虑的状态变量。将式(9)进行Laplace变换可得到Iac(s)、Ip(s)之间的关系为

(a1s4+a2s3+a3s2+a4s+a5)Ip(s)=

(b1s2+b2s+b3)Iac(s)

(10)

进而获得如下传递函数

(11)

其中

(12)

(13)

为了获得更为精准的系统离散模型，经过分析比较，选用Tustin法对式(11)进行离散化处理。处理后得到如下关系式(Iac(z)、Ip(z)分别为iac、ip的Z变换)

(14)

其中

(15)

(16)

式中，c=2/T，T为采样周期。

将式(14)进行反变换可构建出IPT系统的一组差分方程

(17)

最终可得到IPT系统的数据矩阵及过程参数矢量

(18)

(19)

(20)

3 仿真分析及实验验证

为了验证本文提出的负载辨识方法，基于Matlab/Simulink仿真平台建立系统仿真模型，并基于主电路拓扑搭建实验系统，其中一、二次谐振回路的主要参数见表1。

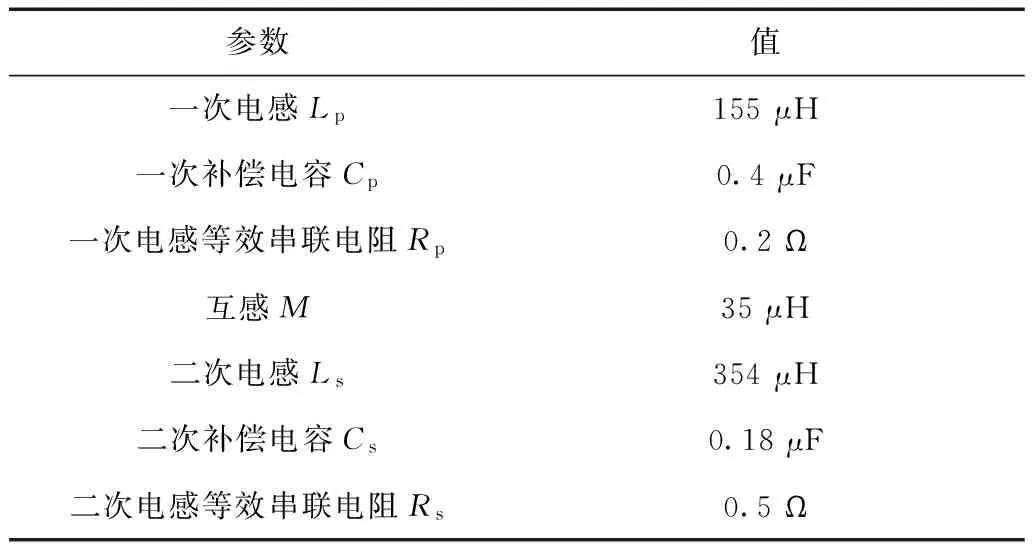
表1 IPT系统仿真及实验参数Tab.1 Parameters of IPT System

以负载大小为30 Ω及50 Ω的情况为例进行仿真及实验验证。图3、图4分别给出逆变器输出电流iac及谐振电流ip的仿真波形及实验波形。可以看出，iac为近似交变方波，ip为正弦波，与图2的分析结果一致。在负载大小为30 Ω、50 Ω的情况下，对图3、图4中所示的状态变量iac、ip进行采样，分别进行50次辨识。为了简化计算，通常将数据矩阵构建为方阵，因此这里数据长度L取值为9。

为了便于对比，图5a、图5b分别给出了负载值为30 Ω、50 Ω时50次仿真及实验负载辨识结果的统计图。由图5可得出，当负载值为30 Ω时，仿真结果中误差率在5%以内的占97%，相对的，实验结果误差较大，其误差率在5%以内的辨识结果占91%；当负载值为50 Ω时，仿真结果和实验结果误差率在5%以内的比例分别为94%及88%。

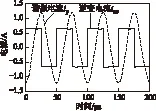
图3 一次谐振电流及逆变电流仿真波形Fig.3 Simulation waveforms of resonant current and inverter current in the primary side

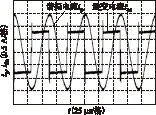
图4 一次谐振电流及逆变电流实验波形Fig.4 Experimental waveforms of resonant current and inverter current in the primary side

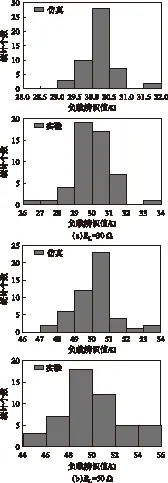
图5 负载辨识结果分布Fig.5 Distributing of load detection results

为了更直观地表明辨识准确度的平均水平，表2进一步给出了上文获得的负载辨识仿真及实验结果的数据分析。

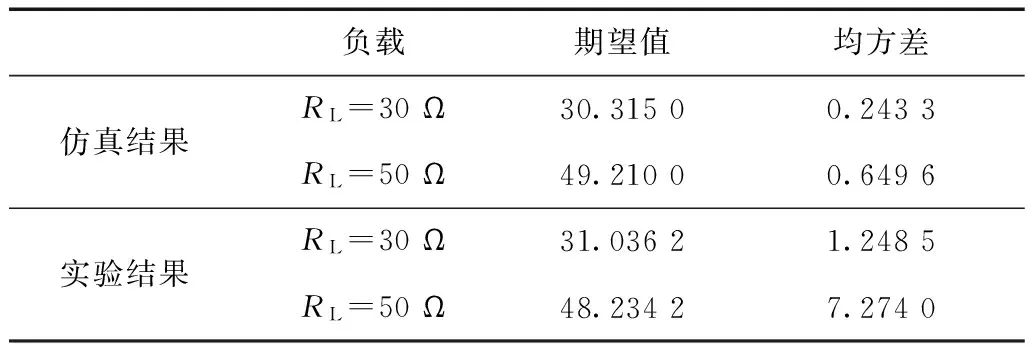
表2 负载辨识结果分析Tab.2 Results analysis of system

由表2可知，当负载RL分别为30 Ω和50 Ω时，仿真得到负载辨识结果期望值的误差率分别为1.05%和1.58%，实验得到负载辨识结果期望值的误差率分别为3.45%和3.53%。因此，在多次辨识后，对得到的数据进行分析，并取其期望值作为最终负载辨识结果能显著提高结果的准确度。另外，通过图5及表2可看出实验结果的分布区间较宽、总体均方差较大、辨识结果误差较大，这是由于噪声干扰、实验仪器的误差及算法存在一定误差等原因造成。

显然，辨识次数与辨识结果的误差率之间存在一定规律，在实际应用中应根据不同情况选择不同的辨识次数。图6通过仿真给出了当负载RL分别为30 Ω及50 Ω时，辨识次数与负载辨识结果误差率之间的规律。

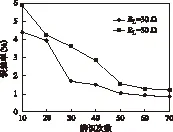
图6 负载辨识结果误差率比较Fig.6 Error rates comparisons

从图6可看出，随着辨识次数的增加，误差率逐渐下降。值得注意的是，当辨识次数达到50次时，误差率下降曲线逐渐平滑。因此，在实际应用中如需较高的辨识准确度，辨识次数选择50次即可满足，继续增加辨识次数不但不再使误差率有显著下降，反而会增加计算成本，影响辨识的实时性。相反，如需较快的辨识速度，可根据实际情况降低辨识次数，当然这样也会相应的降低辨识准确度。

4 结论

本文通过对感应式无线电能传输系统建模分析，完成其数据矩阵的构建，并以此为基础利用最小二乘法完成负载辨识。针对系统运行中因负载变化而增大系统控制难度的问题，提出一种实时的负载辨识方法。仿真及实验结果表明该辨识方法具有较高准确度，并通过仿真给出了辨识次数和辨识结果误差率之间的关系。该方法对于其他结构类型IPT系统的负载辨识具有参考价值。

[1] 黄学良，谭林林，陈中，等.无线电能传输技术研究与应用综述[J].电工技术学报，2013，28(10)：1-11. Huang Xueliang，Tan Linlin，Chen Zhong，et al.Review and research progress on wireless power transfer technology[J].Transactions of China Electrotechnical Society，2013，28(10)：1-11.

[2] Covic G A，Boys J T.Inductive power transfer[J].Proceedings of the IEEE，2013，101(6SI)：1276-1289.

[3] Hui S Y R，Ho W W C.A new generation of universal contactless battery charging platform for portable consumer electronic equipment[J].IEEE Transactions on Power Electronics，2005，20(3)：620-627.

[4] Si Ping，Hu A P，Malpas S，et al.A frequency control method for regulating wireless power to implantable devices[J].IEEE Transactions on Biomedical Circuits and Systems，2008，2(1)：22-29.

[5] 周煜，于歆杰，程锦闽，等.用于心脏起搏器的经皮能量传输系统[J].电工技术学报，2010，25(3)：48-53. Zhou Yu，Yu Xinjie，Cheng Jinmin，et al.Transcutaneous energy transmission system for cardiac pacemaker[J].Transactions of China Electrotechnical Society，2010，25(3)：48-53.

[6] James Jason E I，Chu Alex，Robertson Daniel，et al.A series tuned high power IPT stage lighting controller[C].IEEE Energy Conversion Congress and Exposition，Phoenix，AZ，2011：2843-2849.

[7] Robertson D，Chu A，Sabitov A，et al.High power IPT stage lighting controller[C].IEEE International Symposium on Industrial Electronics (ISIE)，Gdansk，2011：1974-1979.

[8] 曹玲玲，陈乾宏，任小永，等.电动汽车高效率无线充电技术的研究进展[J].电工技术学报，2012，27(8)：1-13. Cao Lingling，Chen Qianhong，Ren Xiaoyong，et al.Review of the efficient wireless power transmission technique for electric vehicles[J].Transactions of China Electrotechnical Society，2012，27(8)：1-13.

[9] Budhia M，Boys J T，Covic G A，et al.Development of a single-sided flux magnetic coupler for electric vehicle IPT charging systems[J].IEEE Transactions on Industrial Electronics，2013，60(1)：318-328.

[10]Wang Chwei-Sen，Covic G A，Stielau O H.Power transfer capability and bifurcation phenomena of loosely coupled inductive power transfer systems[J].IEEE Transactions on Industrial Electronics，2004，51(1)：148-157.

[11]唐春森，孙跃，戴欣，等.感应电能传输系统多谐振点及其自治振荡稳定性分析[J].物理学报，2011，60(4)：745-753. Tang Chunsen，Sun Yue，Dai Xin，et al.Analysis of multiple resonant operating points and their autonomous oscillation stabilities in inductive power transfer systems[J].Acta Physica Sinica，2011，60(4)：745-753.

[12]Dai Xin，Sun Yue，Tang Chunsen，et al.Dynamic parameters identification method for inductively coupled power transfer system[C].IEEE International Conference on Sustainable Energy Technologies，Kandy，2010：1-5.

[13]戴欣，王智慧，唐春森，等.感应电能传输系统参数辨识与恒流控制[J].重庆大学学报，2011，34(6)：98-104. Dai Xin，Wang Zhihui，Tang Chunsen，et al.Study on constant current control of in ductive power transfer with parameter identification[J].Journal of Chongqing University，2011，34(6)：98-104.

[14]Wang Zhihui，Lv Xiao，Sun Yue，et al.A simple approach for load identification in current-fed inductive power transfer system[C].IEEE International Conference on Power System Technology，Auckland，2012：1-5.

[15]Wang Zhihui，Li Yupeng，Sun Yue，et al.Load detection model of voltage-fed inductive power transfer system[J].IEEE Transactions on Power Electronics，2013，28(11)：5233-5243.

A Load Identification Method for Inductive Power Transfer System Based on the Least Squares Algorithm

SuYugang1ChenLong1WangZhihui1AiguoPatrickHu2DaiXin1

(1.Automation college of Chongqing University Chongqing 400030 China 2.Department of Engineering The University of Auckland Auckland 1010 New Zealand)

Identifying load parameters is essential to establishing an efficient，reliable and stable inductive power transfer (IPT) system.Additionally，it is the key problem to achieve optimal efficiency tracking control.This paper focuses on the parallel-serial-(PS)-type current-fed IPT system and the data matrix can be constructed by setting up high order nonlinear differential equations of the system.The load identification problem is then transformed in to the system parameter identification problem，which is solved by the acquisition of the system process parameters vector based on the least squares algorithm.Finally，the simulations and the experiments can verify the feasibility of the proposed method.

Inductive power transfer，least squares algorithm，load identification

国家自然科学基金(51477020，51377183)和国家自然科学青年基金(51207173)资助项目。

2014-11-06 改稿日期2015-01-10

TM724

苏玉刚 男，1962年生，博士，教授，研究方向为无线电能传输技术、电力电子技术、控制理论应用与自动化系统集成。(通信作者)

陈 龙 男，1989年生，博士研究生，研究方向为电力电子技术和无线电能传输技术。