二次双曲Bézier曲线曲面*

严兰兰，韩旭里，周其华

(1.东华理工大学理学院,江西 南昌 330013;2.中南大学数学与统计学院,湖南 长沙 410083)

二次双曲Bézier曲线曲面*

严兰兰1,2，韩旭里2，周其华1

(1.东华理工大学理学院,江西 南昌 330013;2.中南大学数学与统计学院,湖南 长沙 410083)

为了简化构造组合曲线时，相邻曲线的控制顶点间应满足的光滑拼接条件, 构造了一种结构类似于二次Bézier曲线的含参数的双曲型曲线，称之为H-Bézier曲线。该曲线具有Bézier曲线的许多基本性质, 如凸包性、对称性、几何不变性、端点插值和端边相切性。另外，该曲线具备形状可调性，可以精确表示双曲线。此外, 若取特殊的参数，则当相邻H-Bézier曲线的控制顶点间满足普通Bézier曲线的G1光滑拼接条件时, 曲线在公共连接点处可以达到G3光滑拼接。另外, 给出了构造与给定多边形相切的H-Bézier曲线的方法, 该方法简单有效, 而且整条曲线对给定的切线多边形是保形的。运用张量积方法，将H-Bézier曲线推广后得到的曲面同样具有很多良好的性质。

曲线设计;Bézier曲线; 连续性; 形状参数; 切线多边形

1 引言

Bézier曲线是计算机辅助几何设计中表示曲线的重要工具之一，它具有结构简单、直观等诸多优点。虽然如此，在实际应用中，Bézier曲线依然表现出一些不足。例如，由于单一的Bézier曲线无法表示复杂的形状，所以为了满足实际工程的需求，往往需要构造组合Bézier曲线，而为了保证组合曲线的光滑性，相邻曲线的控制顶点间必须满足一定的连续性条件，一般情况下，对光滑性的要求越高，条件会越复杂，从而难以实现。另外，由于Bézier曲线的形状由其控制顶点唯一确定，所以若要修改曲线的形状，必须改变控制顶点，重新计算曲线方程。第三，Bézier曲线不能表示工程上常用的除抛物线以外的圆锥曲线。

对于Bézier曲线的上述第二、第三个缺点，很多文献提出了解决办法。如文献[1～7]构造了含一个或多个参数的基函数，使得由之定义的曲线在具备Bézier曲线基本性质的同时，还具有形状可调性。文献[8～14]在三角函数空间、双曲函数空间等非多项式空间上构造基函数，使得由之定义的曲线在具备Bézier曲线基本性质的同时，还能表示一些圆锥曲线和超越曲线。但是，对于Bézier曲线的上述第一个不足，很少有文献专门对其进行研究。

为了同时克服Bézier曲线的上述三个不足，也就是说使曲线既具有形状可调性，又能精确表示某种特殊曲线，还能够在相对简单的条件下实现更高阶的光滑拼接，本文构造了一种结构类似于二次Bézier曲线的带形状参数的新曲线。该曲线不仅保留了普通Bézier曲线的诸多优良性质，而且可以通过选择不同的形状参数来得到由相同控制多边形所确定的不同的曲线，无需有理形式便能精确表示双曲线。更重要的是，选择特定的形状参数时，在普通Bézier曲线的G1光滑拼接条件下，该曲线可以达到G3光滑拼接。

2 基函数及其性质

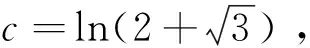
(1)

为二次双曲Bernstein基函数，简称H-Bernstein基。

图1所示为H-Bernstein基的图形，其中实线、虚线、点线分别为a0(t)、a1(t)、a2(t)的图形。图1a中取参数λ=1，图1b中取参数λ=2。

Figure 1 H-Bernstein bases

H-Bernstein基具有类似于Bernstein基的一些良好性质，具体有：

(1)非负性：对任意的t∈[0,1]，有ai(t)≥0，i=0,1,2。

(3)对称性：对任意的t∈[0,1]，有ai(t)=a2-i(1-t),i=0,1,2。

(4) 端点性质：对任意的λ∈[1,2]，有:

(2)

当λ∈[1,2)时，有:

(3)

当λ=2时，有:

(4)

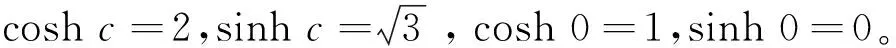
a0(0)=(coshc-1)λ=1

a2(0)=(cosh 0-1)λ=0

又由a0(0)+a1(0)+a2(0)=1得a1(0)=0，因此式(2)中结论(a)得证。再由ai(t)=a2-i(1-t),i=0,1,2知:

ai(1)=a2-i(0),i=0,1,2

(5)

由式(5)和(2)中式(a)即可得式(2)中结论(b)。

当λ=2时，由式(1)经过求导计算可得:

令上式中t=0,可得:

(6)

又由a0(t)+a1(t)+a2(t)=1可得:

(7)

由式(6)和式(7)式可得:

因此，式(4)中结论(a)、(c)、(e)得证。再由ai(t)=a2-i(c-t),i=0,1,2可知:

(8)

由式(8)和式(4)中(a)、(c)、(e)式即可得式(4)中结论(b)、(d)、(f)。

□

3 曲线及其性质

3.1 曲线的定义与性质

定义2 给定三个控制顶点Vi∈Rd(d=2,3;i=0,1,2)，称:

(9)

为二次双曲Bézier曲线，简称H-Bézier曲线。

由H-Bernstein基的性质，易知H-Bézier曲线具有类似于Bézier曲线的一些性质，具体有：

(1) 凸包性。由H-Bernstein基的非负性和规范性可知，H-Bézier曲线位于其控制顶点形成的凸包内。

(2) 几何不变性与仿射不变性。由H-Bernstein基的规范性可知，一方面，H-Bézier曲线的形状仅依赖于控制顶点，几何变换不改变曲线的形状；另一方面，对控制多边形进行缩放或错切等仿射变换，所对应的新曲线就是原曲线经过相同仿射变换后的曲线。

(3) 对称性。由H-Bernstein基的对称性可知，取相同的参数λ时，由控制多边形V0V1V2和V2V1V0所生成的曲线形状是相同的，只是方向相反。

(4) 端点性质。由H-Bernstein基的端点性质和H-Bézier曲线的表达式可知，在H-Bézier曲线的端点处有:

a(0)=V0,a(1)=V2

(10)

当λ∈[1,2)时，有:

(11)

当λ=2时，有:

(12)

(5) 形状可调性。由于H-Bernstein基的表达式中含有参数λ，选择不同的λ值，可以得到不同的基函数，因此即使固定控制顶点，依然可以通过改变参数λ的值来调整曲线的形状。

图2所示为由相同控制顶点和不同参数所确定的H-Bézier曲线(实线，从上到下依次取参数λ=2,1.3,1)与普通二次Bézier曲线(虚线)。从图2中可以看出，H-Bézier曲线对控制多边形的逼近性优于Bézier曲线。

Figure 2 H-Bézier curves and Bézier curves

3.2 双曲线的表示

Figure 3 Hyperbola expressed by the H-Bézier curve

3.3 组合曲线的连续性

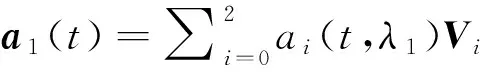
(13)

则当λ1、λ2∈[1,2]且λ1、λ2不同时等于2时，两曲线G1连续；当λ1=λ2=2时，两曲线G3连续。

证明 只证明λ1=λ2=2时的结论，另一种情况的结论类似可得。由式(10)和式(12)可知:

(14)

要使两曲线G3连续，必须:

(15)

其中β1、β2、β3为参数，且β1>0(见文献[15])。 将式(14)代入式(15)并整理，得到:

(16)

要使式(16)中的关系式(b)～(d)同时成立，只需取:

即可。记C=β1，故当式(13)成立时，若λ1=λ2=2，则两曲线G3连续。

□

对于普通Bézier曲线和大多数文献中给出的扩展Bézier曲线而言，在式(13)所给条件下，相邻曲线间只能达到G1连续。而对于H-Bézier曲线而言，取特殊参数时却能达到G3连续。 图4所示为由两条H-Bézier曲线段构成的G3连续的组合曲线。

Figure 4 Composite H-Bézier curve of G3 continuity

3.4 曲线的应用

给定闭多边形P0,P1,…,Pn(P0=Pn)，下面分析如何构造一条封闭的组合H-Bézier曲线，使之与给定闭多边形的每一条边都在指定点相切[16]。假设闭多边形的第i条边上的切点为:

Ti=(1-ki)Pi-1+kiPi

(17)

其中，ki∈(0,1)(i=1,2,…,n)为切点调节参数。

为了实现上述目标，首先增加一个虚拟切点Tn+1=T1，然后在每两个相邻的切点Ti和Ti+1之间构造一条H-Bézier曲线段ai(t)，这里i=1,2,…,n。因此，整条组合H-Bézier曲线由n条曲线段组成。取第i条曲线段:

(18)

的控制顶点为:

Vi0=Ti,Vi1=Pi,Vi2=Ti+1

(19)

由式(10)～式(12)和式(17)～式(19)可知:

ai(0)=Ti,ai(1)=Ti+1,

(20)

由式(20)可知，第i条H-Bézier曲线段与给定闭多边形相切于点Ti和Ti+1。另外，由定理1可知，当所有λi∈[1,2)且不同时等于2时，相邻H-Bézier曲线段在连接点处G1连续；当所有λi=2时，相邻H-Bézier曲线段在连接点处G3连续。

这里提供的构造与给定多边形相切的曲线的方法具有以下优点：

(1) 曲线的所有控制顶点直接由给定闭多边形的顶点和切点确定，无需其它的计算；

(2) 相邻曲线段在连接点处G1连续或G3连续，可以满足工程上的大部分需求；

(3) 曲线中含有形状参数，并且不同曲线段可以取不同的参数，因此曲线的形状可以局部调整；

(4) 由于H-Bézier曲线段不存在拐点，且曲线的凹凸性与控制多边形一致，所以整条曲线对给定的切线多边形是保形的。

图5所示为与给定多边形相切于指定点的H-Bézier曲线。 图中点线为给定的切线多边形，打星号的点为指定的切点，实线为H-Bézier曲线。图5a中所有λi=1，图5b中所有λi=2。

Figure 5 H-Bézier curves with given tangent polygon

4 H-Bézier曲面

定义3 给定呈拓扑矩形阵列的控制顶点Vij∈R3(i,j=0,1,2)以及参数λu、λv∈[1,2]，称：

为H-Bézier曲面，其中ai(u,λu)、aj(v,λv)(i,j=0,1,2)分别为含参数λu、λv的H-Bernstein基。

H-Bézier曲面具有与H-Bézier曲线类似的性质，如凸包性、几何不变性、对称性等。另外，对于两张H-Bézier曲面：

而言，当Ri0=Vi2(i=0,1,2)时，两曲面G0连续，当Ri1-Ri0=C(Vi2-Vi1)(C>0)(i=0,1,2)时，若λi∈[1,2)(i=0,1,2)且不同时为2时，两曲面G1连续；若λi=2(i=0,1,2)，则两曲面G3连续。

图6所示为由两张H-Bézier曲面片构成的组合曲面。图6a中λi=1(i=0,1,2)，两曲面G1连续；图6b中λi=2(i=0,1,2)，则两曲面G3连续。

Figure 6 Composite H-Bézier surface of G3 continuity

5 结束语

H-Bézier曲线不仅具备Bézier曲线的凸包性、几何不变性、对称性等基本性质，而且具备形状可调性，能够精确表示双曲线。此外，若选择参数λ=2，则在构造组合曲线时，只要相邻曲线的控制顶点之间满足普通Bézier曲线的G1光滑拼接条件，曲线间便可以达到G3光滑拼接。另外，用H-Bézier来构造与给定多边形相切的曲线，算法不仅简单而且有效，且曲线对多边形是保形的。下一步的目标是对三次及三次以上的Bézier曲线进行类似的扩展，使曲线可以在简单的条件下实现更高阶的光滑拼接。

[1]PieglL.AgeneralizationoftheBernstein-Béziermethod[J].Computer-AidedDesign, 1984, 16(4):209-215.

[2]WangWen-tao,WangGuo-zhao.Béziercurveswithshapeparameter[J].JournalofZhejiangUniversityScienceA(ScienceinEngineering), 2005, 6(6):497-501.

[3]HanXi-an,MaYi-chen,HuangXi-li.AnovelgeneralizationofBéziercurveandsurface[J].JournalofComputationalandAppliedMathematics, 2008, 217(1):180-193.

[4]YangLian-qiang,ZengXiao-ming.Béziercurvesandsurfaceswithshapeparameters[J].InternationalJournalofComputerMathematics, 2009, 86(7):1253-1263.

[5]QinXin-qiang,ZhangNian-juan,HuGang.AnovelBéziercurvewithmultipleshapeparameters[C]∥Procof2010 3rdIEEEInternationalConferenceonComputerScienceandInformationTechnology, 2010:494-498.

[6]ChenJie,WangGuo-jin.AnewtypeofthegeneralizedBéziercurves[J].AppliedMathematics-AJournalofChineseUniversities, 2011, 26(1):47-56.

[7]YanLan-lan,LiangJiong-feng.AnextensionoftheBéziermodel[J].AppliedMathematicsandComputation, 2011, 218(6):2863-2879.

[8]ChenQin-yu,WangGuo-zhao.AclassofBézier-likecurves[J].ComputerAidedGeometricDesign, 2003, 20(1):29-39.

[9]HanXi-an,MaYi-chen,HuangXi-li.ThecubictrigonometricBéziercurvewithtwoshapeparameters[J].AppliedMathematicsLetters, 2009, 22(2):226-231.

[10]LiJun-cheng,ChenGuo-hua,YangDu-qing.ModifiblequasicubicBéziertrgonometriccurves[J].ComputerEngineering&Science, 2010, 32(3):69-71.(inChinese)

[11]HanXu-li,ZhuYuan-peng.Curveconstructionbasedonfivetrigonometricblendingfunctions[J].BITNumericalMathematics, 2012, 52(4):953-979.

[12]SuBen-yue,ShengMin.Bézier-likecurvesandsurfacesbasedonhyperbolicfunctions[J].ComputerEngineeringandDesign, 2006, 27(3):370-372.(inChinese)

[13]XieJin,TanJie-qing.Quadratichyperbolicpolynomialcurveswithmultipleshapeparameters[J].JournalofImageandGraphics,2009,14(6):1206-1211.(inChinese)

[14]ZhangJin-xiu,Tanjie-qing.ExtensionsofhyperbolicBéziercurves[J].JournalofEngineeringGraphics, 2011, 32(1):31-38.(inChinese)

[15]ShiFa-zhong.Computeraidedgeometricdesign&NURBS[M].Beijing:HigherEducationPress, 2001.(inChinese)

[16]LiuZhi,TanJie-qing,JiangPing,etal.ClosedC2-continuousquarticgeneralizedballcurveswithgiventangentpolygons[J].HigherSchoolJournalofComputationalMathematics, 2012, 34(3):231-237.(inChinese)

附中文参考文献：

[10] 李军成, 陈国华, 杨笃庆. 可调的类三次Bézier三角曲线[J]. 计算机工程与科学, 2010, 32(3):69-71.

[12] 苏本跃, 盛敏. 基于双曲函数的Bézier型曲线曲面[J]. 计算机工程与设计, 2006, 27(3):370-372.

[13] 谢进, 檀结庆. 多形状参数的二次双曲多项式曲线[J]. 中国图象图形学报, 2009, 14(6):1206-1211.

[14] 张锦秀, 檀结庆. 代数双曲Bézier曲线的扩展[J]. 工程图学学报, 2011, 32(1):31-38.

[15] 施法中. 计算机辅助几何设计与非均匀有理B样条[M]. 北京:高等教育出版社, 2001.

[16] 刘植, 檀结庆, 江平, 等. 与给定多边形相切的C2四次广义Ball闭曲线[J]. 高等学校计算数学学报, 2012, 34(3):231-237.

YAN Lan-lan,born in 1982,PhD candidate,lecturer,her research interest includes computer aided geometric design.

韩旭里(1957-),男,湖南武冈人，博士，教授，研究方向为计算机辅助几何设计。E-mail:xlhan@csu.edu.cn

HAN Xu-li,born in 1957,PhD,professor,his research interest includes computer aided geometric design.

Quadratic hyperbolic Bézier curve and surface

YAN Lan-lan1,2，HAN Xu-li2,ZHOU Qi-hua1

(1.College of Science,East China Institute of Technology,Nanchang 330013;2.School of Mathematics and Statistics,Central South University,Changsha 410083,China)

When composite curves are constructed, the control points of the adjacent curves must meet certain conditions. In order to simplify the conditions, a kind of hyperbolic polynomial curve with parameters, called H-Bézier curve, which has a structure similar to the quadratic Bézier curve, is constructed. This curve has many basic properties of Bézier curve, such as convex hull property, symmetry, geometric invariance, endpoint interpolation and end edge tangent property. Besides, the curve has shape adjustability and can represent hyperbola. If special parameters are chosen, then when the control points of two adjacent curves satisfy the conditions for Bézier curve, they can achieve continuity. In addition, the method of constructing H-Bézier with given tangent polygon is given. This method is simple and effective, and the entire curve is conformal to the tangent polygon. Using tensor product method, the H-Bézier curve can be extended to surface, which also has many good properties.

curve design;Bézier curve;continuity;shape parameter;tangent polygon

1007-130X(2015)01-0162-06

2013-03-12;

2013-08-26基金项目：国家自然科学基金资助项目(11261003,11271376,60970097);江西省教育厅科技项目(GJJ14493)

TP

A

10.3969/j.issn.1007-130X.2015.01.025

严兰兰(1982-),女,湖北浠水人,博士生，讲师，研究方向为计算机辅助几何设计。E-mail:yxh821011@aliyun.com

通信地址：330013 江西省南昌市经开区广兰大道418号东华理工大学理学院

Address:College of Science,East China Institute of Technology,418 Guanglan Avenue,Economic and Technological Development Zone,Nanchang 330013,Jiangxi,P.R.China