电磁学与电动力学中的磁单极—Ⅲ
2015-03-27王青
王 青
(清华大学物理系,北京 100084)
教学研究
电磁学与电动力学中的磁单极—Ⅲ
王 青
(清华大学物理系,北京 100084)
本文为作者磁单极系列文章的第3篇,该系列文章在电磁学和电动力学框架内用尽量科普的方式分别介绍磁单极的若干奇特性质. 在本篇文章中作者通过一个实例显示有磁单极存在的点电荷系统的作用量涉及磁单极的部分在物理区域是不存在的,但在以物理区域为边界的高维非物理区域可以存在,考虑量子力学则要求点电荷必须是量子化的.
磁单极;最小作用量;高维;全息;电荷量子化
本文是在电磁学和电动力学中讲解磁单极奇妙性质的第3篇文章.在前2篇文章[1,2]中分别介绍了磁单极在角动量方面的角色和作用,以及狄拉克磁单极及其与规范变换的关系;在本文中介绍磁单极在最小作用量原理中所起的特殊作用.本篇内容安排如下: 第1节通过几个具体例子介绍最小作用量;然后在第2节提出本文所主要关心的作用量是否存在的问题,并在第1节讨论的一个例子中证明加进磁单极将导致这个体系的作用量不再存在;最后在第3节讨论作用量不存在会给我们什么深刻的启示.
1 最小作用量原理
对物理系统人们总是选择一些坐标(一般地叫广义坐标,第i个坐标经常被记为qi(t))用其随时间的变化行为来描述体系随时间的演化.例如一个质点我们用它在空间坐标系3个坐标轴上的坐标构成的矢量r(t)来描写,对电磁场则用每个空间点的标量势φ(r,t)和矢量势A(r,t)来描写,等等.在经典物理学中,这些坐标满足某个对时间的二阶微分方程,如自由运动的质点满足,
这些关于时间的微分方程通常叫体系的运动方程,给它们加上初始条件(一般是初始的坐标和速度值,对像电磁场这样的具有无穷多自由度的体系通常还要补充相应的边界条件)就完全把体系坐标随时间的变化行为唯一地确定下来.这种用微分方程加初始条件确定体系运动规律的方式是日常描述一个体系的习惯和标准的做法.它不仅适用于物理体系,世上很多其他系统诸如经济运转,人口变化等只要有确定的随时间变化的描写变量的体系,原则上都可以采用此类方式来描述.探寻和理解这些体系随时间演化的规律因此转变为寻找和解释为什么这些体系会选择如此样子的运动方程.至少在众多可能候选的微分方程中,对某个确定的体系为什么选择某种特定的方程一下子是看不出来的.
最小作用量原理不用微分方程而用极值原理来描写一个体系随时间演化的规律.它的表述是: 对每一个物理体系都存在一个由其广义坐标及其微商构造的泛函;这个体系的实际运动总是使这个泛函取极小值.例如对前面提到的自由运动的质点,最小作用量原理就说此体系存在一个拉格朗日量L,
其中积分的上下限分别为粒子运动的起始和终了时刻.不难证明,让式(3)取极值即可得到由式(1)给出的微分方程.
进一步如果这个粒子带电荷q,并且在由标量势φ和矢量势A描写的外电磁场中运动,则体系的拉格朗日量变为
把式(4)代入式(3)再求极值即可得到点电荷的运动方程
在式(5)中进一步定义
我们发现此点电荷所受的力就是通常的洛伦兹力.
如果此带电粒子不在外电磁场中运动(因而拉氏量式(4)中没有与标量势φ和矢量势A相关的项),而被限制在一个半径为单位长度(r=1)的一个球面上运动(如图1所示).

图1 约束在球面上的质点
这个体系的作用量应该就是把式(2)代入式(3)得到的结果,只不过在求极值时要额外考虑到约束条件.数学上有一个拉氏乘子方法可以避免在求极值时再考虑约束条件,只要把约束方程乘以一个独立参数λ加进拉格朗日量即可,即
由此代入式(3)并对坐标求极值得到运动方程:
方程右边是对应把质点约束在球面上所需要的力,其中存在一个未知参数λ.为确定它,将约束条件(它可以通过把式(7)代入式(3)并对参数λ求极值得到)对时间求2次导数,得到
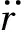
从以上几个例子可以看到对我们熟知的粒子运动(如前面讨论的自由质点和在外电磁场中的带电点粒子)都可以找到相应的作用量,其运动方程是对作用量求极值的导出物,而不是原始理论计算的出发点.甚至对有约束的系统,其运动方程也可被看作是作用量极值的产物.由此可以把原来
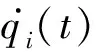
这个方程也叫拉格朗日方程,它在原来微分方程体系中被作为体系原始出发点的第一原理.
2 作用量的存在性
既然最小作用量原理可以替代运动方程作为第一原理,那么要描述任意一个体系随时间的演化规律,只需找到其相应的作用量即可.这里可能会有一个问题:是否对任意一个系统都存在有相应的作用量?为了方便,姑且假设这个体系随时间的演化是可以用微分方程来描写的,这个体系不一定非得是物理体系.或者换句话说,是否任何一组微分方程(假设它描述某个系统的时间演化规律)都可化成为方程(11)的形式?如果可以就意味着存在拉格朗日量,因此由式(3)也就存在作用量.这个问题看起来有点数学化,因为作用量作为一个数学量(而不是物理实体),其存在性的讨论似乎应属于数学的范畴.如果对此问题的回答是肯定的,那就意味着任何一个微分方程都等价于一个极值问题,对有确定规律(也就是存在微分方程描述)的体系的看法就都等价于其存在某种极值,因而最小作用量原理升格成放之四海而皆准的普世原则,那好像挺不错的.如果对此问题的回答是否定的,那就比较奇怪了.因为我们所熟知的物理系统基本都是具有作用量的,如果某个特定体系作用量真不存在,它一定十分有别于我们熟知的系统,那里也许应该有什么奇异的事情发生……?
笔者的学生很多年前在南开大学开会时有幸问过陈省身先生此问题,回答是否定的,陈先生还说了一堆学生无法听懂的理由.学生最后反馈回来说只是了解到如果体系有某种特别的性质好像是某种对称性,就会有运动方程存在而作用量不存在的现象.鉴于此信息,笔者当时的理解是: 那些不存在作用量的体系很可能是一些十分怪异的纯数学系统,所有物理体系都应该存在作用量.如果是这样,即使找到不存在作用量的体系也与物理无关,因而对我们做物理研究不会有什么影响.后来某天读到获得菲尔兹奖的知名物理学家E.Witten的著名文章[3],才发现原来在物理体系里也存在这样的系统,作用量在其中不存在!本文以下的大部分讨论都来自Witten的文章,我们略去了量子场论的复杂讨论而只局限在电磁学和电动力学的范围内进行讨论.
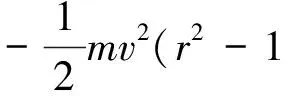
选择合适的磁荷单位可以使这个磁单极产生的磁感应强度为
注意在球面上的质点带电荷q,在其作受限运动的球面上,原来的运动方程式(10)中现在还应包括洛伦兹力的贡献,即
其中使用了约束条件r2=1.式(13)是描述限制在单位球面上带电荷q质量为m的质点的运动方程,方程右边第一项是把质点约束在球面上的约束力,第二项是磁单极场产生的洛伦兹力.现在对这个系统,运动方程有了,是否存在作用量?
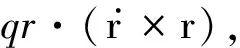
且慢!有些仔细的读者会说,不对呀!对在外电磁场中运动的带电粒子,你不是在式(4)中给出了一个拉格朗日量,怎么能说不存在拉格朗日量呢? 只要把式(4)给出的反映外电磁场的项-qφ+q·A写出来不就是了吗? 我们看看真把这项写出来会咋样.对第1项,磁单极不会产生标量势因而它恒为零;对第2项需要写下磁单极所贡献的矢量势,但如本系列第2篇文章[2]所讨论的,对磁单极来说矢量势是奇异的,或者说它无法在全空间很好地定义.或者再明确一点地说式(12)给出的磁感应强度满足方程▽·B=δ(r),其中等号右边是反映具有单位磁荷的磁单极的磁荷密度的δ函数.而另一方面由矢量势和磁感应强度的关系B=▽×A,可以得到▽·B=0.这明显和前面具有磁单极的式子相互冲突,唯一的可能性是矢量势在一些地方没有很好地定义,导致公式B=▽×A不在全空间处处适用.事实上,如果强行要求矢量势在全空间处处可微,则会导出一些极为奇怪的结果,例如这时可以利用著名的亥姆霍兹定理(这个关系实际上是一个恒等式,如果不熟悉它可以跳过下面的两组式子直接阅读其后的内容)
其中第1项通常叫矢量势的纵场部分,它可以通过在本系列第2篇文章[2]中重点研究的规范变换给完全变换掉因而为零;第2项叫矢量势的横场部分,下面证明对式(12)给出的磁单极它也为零,
因此假设矢量势在空间处处可微,结合规范变换得到式(12)给出的磁单极的矢量势在空间可以处处为零.
以这样看,即使按照式(4)强行写下一个拉格朗日量并代入式(3)给出相应的作用量,这个作用量也是有奇异没能很好定义的作用量.更准确的陈述应该是: 对这个系统全空间很好定义的作用量不存在!进一步,由于我们已经把讨论的体系限制在了单位半径的球面上,这时实际上并不真正要求矢量势在全空间都有很好的定义,而只要求其在球面上有很好的定义就可以了.遗憾的是,即使这样退而求其次的要求也是达不到的,因为它使得下面在球面上的面积分产生矛盾的结果:
其中第一个等号成立是因为按照格林公式此等号右边的积分应该等于在积分曲面的边界曲线上曲线积分,而目前由于是封闭曲面,没有边界曲线或者说边界曲线的长度为零(可以看成是一个缩小为一个点的边界),因而在边界上的曲线积分为零.在第4个等号后我们应用了此磁场是来自于位于球心的磁单极的条件.从上面结果看即使在这简化了的球面上,矢量势仍是无法很好定义的,因而用势定义的作用量在球面上似乎仍是不存在的!如前所述,这样的事情发生一定意味着有什么更深刻的内涵.请见下节的讨论.
3 出现磁单极导致不存在作用量体系的启示
上节讨论了一个在球心具有单位磁荷的磁单极、限制在单位球面上电荷q质量为m的质点系统,对此质点来说它的运动范围被限制在三维空间的一个二维球面上,它自己的运动实际上是这个二维球面上的一条曲线,即它的实际运动轨迹是一维的,具体运动轨迹由方程(13)决定.我们发现这个系统的作用量是不存在的,如果非要强行写下来它的作用量应该是
它由于矢量势无法定义因而也是没有很好定义的.既然此系统作用量不存在,它一定会有某些特别之处,深度挖掘也许会给我们有价值的启示.首先注意到作用量式(14)实际并未涉及所讨论的球面的全部,而只是球面上涉及质点所走过的曲线.因此由上节中证明的矢量势在整个球面上没有很好的定义,所导出的作用量没有很好的定义实际上并不真的发生在整个球面上,而只是在球面上质点所走过的曲线上没有很好定义.
为了能继续深入下去,考虑一个子情形: 其中粒子在球面上走了一个闭合回路γ,也就是r(t初始)=r(t结尾),具体如图2所示.
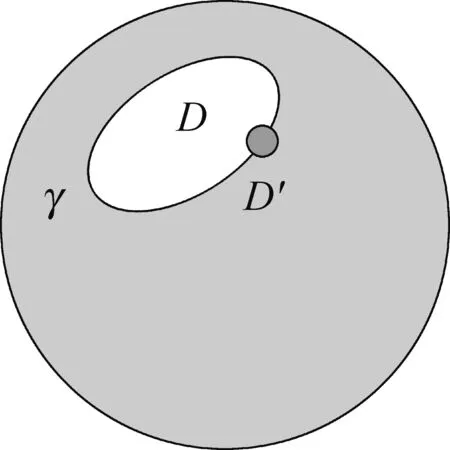
图2 在球心有磁单极的单位球面上的带电质点走过了闭合回路γ
由于粒子走的是闭合路径,这个回路γ就把球面分割成为D和D′两个区域.而作用量中出问题的涉及磁单极贡献的矢量势的最关键项可以写为
其中由于r(t初始)=r(t结尾) ,积分变成一个回路积分,因而可以利用格林积分公式把在回路γ上的曲线积分转化为回路所包围的表面D上的曲面积分,而被积函数相应地转变为矢量场的旋度,也就是磁感应强度.虽然矢量势是奇异的,但最后结果并不依赖它,而只依赖一个没有奇异被很好定义的磁感应强度.把式(15)代回式(14),发现对粒子走一个回路的情形,作用量不是不存在或不能很好定义的,而是存在且能很好定义的量,
代价是此质点系统的描述不再只局限在它所运动的路径γ上了,它与磁单极相关的部分必须被扩充到它所没走过的区域D,而γ只是D的边界.从这个角度看,在球面上,虽然矢量势没有很好定义,但作用量确能够很好定义,只不过是超出了质点所走的路径.如何理解这个结果?
首先,作用量按其原始定义都只存在于坐标所经历的区域,对粒子来说就是在它所走过的路径上,此路径对目前的系统是一维的.超出这个区域意味着要用非坐标所经历的区域(姑且把它定义为非物理区,对应坐标经历的区域叫物理区)的东西来表征在物理区里所展示的物理,对目前的系统就是要用延展到粒子所没走过的二维表面D上的磁场来表征在轨道γ上运动的粒子涉及磁单极部分的作用量.这隐含了两层意思: 对涉及磁单极部分的作用量,一是物理区域(目前即为粒子所走的路径)自己在作用量层面上已经无法有效地描述自己的运动了(体现为作用量不存在),非需要非物理区域(目前就是粒子足迹未曾踏及的区域D)的某些东西的介入.再有就是在目前系统从物理区域到非物理区域涉及了空间维数的升高,
原本物理一维曲线上的事务现在需要在非物理的二维曲面上办理才可以.
再有在目前这个系统中,对涉及磁单极部分的作用量,这个一维不存在作用量的区域和二维存在作用量的区域的联系是,一维物理区域是二维非物理区域的边界,这体现了某种全息性: 二维不可观察(也就是粒子没有踏及)的非物理区的信息全都最后以实际的粒子运动展现在了一维可观察(粒子真实走过)的物理区内,即大范围区域的信息在小范围区域展示.到此为止,好像我们被启发了一些似是而非的“洞见”.这些结果在当今量子场论最前沿的进展中有进一步的发展,我们不在这里介绍.
故事还不止于此,注意到在图2中D和D′两个区域实际上是对称的,在应用格林公式时结果既可表达在D上,也可表达在D′上,表达式由于回路正方向和曲面法向相同或相反会导致相差一个负号.这两个区域的结合会导致更奇葩的结果.首先利用
这实际上是磁场的高斯定理,它把在区域D上的磁单极所产生的磁通量与在D′上的磁通量关联起来了,
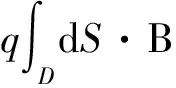
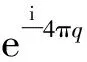
这样又得到在第一篇文章[1]中所得到的电荷量子化条件.我们发现只要涉及磁单极和量子力学,电荷就要量子化!
4 结语
磁单极存在导致在物理区域不存在的涉及磁单极的作用量可以在延拓到以物理区域作为边界的高维非物理区域存在,并且考虑到量子力学则要求电荷是量子化的.
[1] 王青.电磁学与电动力学中的磁单极——I[J]. 物理与工程,2013,23(6): 8-11.
[2] 王青.电磁学与电动力学中的磁单极——II[J]. 物理与工程,2013,24(5): 29-33.
[3] Witten Edward. Global aspects of current algebra [J]. Nucl Phys, 1983, B223: 422-432.
祝贺张晓光教授荣获“北京高校教学名师奖”
近日,北京邮电大学理学院张晓光教授被评选为“第十一届北京市高等学校教学名师”.作为基础物理教师和光纤通信专家,他将基础物理教学工作与光纤通信科研工作完美结合,走出了一条教学与科研相互促进,教学成果与科研成果双丰收的学术之路.
张晓光教授1994年和1996年在我刊发表《普通物理教材中氦氖能级图的一些问题》和《利用波叠加观点讨论光波导模式的物理意义》;今年还应编辑部特约在第3期发表2015国际光年专题文章之一《光纤偏振控制研究:从理论和实验到应用》,同期彩页上还发表了《风采实录:张晓光教授和他的教学与科研并重之路》.
《物理与工程》编辑部
MAGNETIC MONOPOLE IN ELECTROMAGNETISM AND ELECTRODYNAMICS—Ⅲ
Wang Qing
(Department of Physics, Tsinghua University, Beijing 100084)
This is the third paper in the series of magnetic monopole. These series include four individual papers. They discover some peculiar properties of magnetic monopole which will be introduced as popular science in the frameworks of electromagnetism and electrodynamics. In this particular paper, we use an example to illustrate the presence of a magnetic monopole and the action relate to magnetic monopole do not exist in the physical region for a point charge system, however it can exist in a higher dimension non-physical region where the physical region is the boundary of non-physical region. Also, the charge is quantized if we put quantum mechanics into consideration.
magnetic monopole; least action; high dimension; holography; charge quantization
2015-05-21
王青,男,教授,主要从事理论物理的科研和教学工作,研究方向为量子场论与基本粒子理论.wangq@mail.tsinghua.edu.cn
