具有脉冲接种和垂直传染的时滞SEIVR乙肝模型

宋运娜，何兰，滕辉

（齐齐哈尔医学院高数教研室，黑龙江 齐齐哈尔 161006）

0 引言

乙型肝炎病毒（HBV）一直在全球范围内广泛流行，我国是乙型肝炎高发国家之一，全国有1.2亿人长期携带乙肝病毒，1988年世界卫生组织将全球新生儿乙肝免疫作为控制乙肝疾病的重要措施.我国在1992年将乙肝疫苗纳入计划免疫.2006年国家卫生部公布乙肝病毒表面抗原携带从1992年的9.75%降至7.18%.乙肝疫苗接种在预防乙肝病毒感染中发挥重要作用.

中外学者从多角度做了大量的研究，杨金根［1-2］在脉冲接种乙肝模型中，将易感者根据有无不良行为分为两类并研究了具有垂直传染、脉冲接种的乙肝模型；罗丽丽［3］讨论了微观状态下，乙肝疫苗接种后体液的免疫应答模型；LuJiu［4］研究了季节变化对肺结核病的影响；Store L等［5］从理论上分析了常数接种和脉冲接种对传染病研究的影响；Alberto d’Onofrio［6］给出了带有脉冲接种在SEIR模型的稳定结果；Zhou Y等［7］研究了接种后的免疫人群存在的模型.

本文中讨论了一类SEIVR乙肝传染病模型，人群中分出接种者V，接种者不能马上具有免疫力，因接种而具有的免疫力也可能丧失；疾病潜伏者分为两类，一类染病初期处于潜伏期的E1；另一类染病后期继而出现的一种转移状态R1＞1,R2＞1，转移状态类是介于染病者和恢复者之间的状态，携带病毒但已经不具有传染性.R3＞1为易感者，I为染病者，R为恢复者，假设易感者的染病率为β，接种者没有获得完全免疫力时的染病率为β1，自然死亡率为μ，因病死亡率是μ1，接种者获得完全免疫力的比率θ，疾病恢复率k1，染病者进入转移状态的比率k2，由转移状态转变成为恢复者的比率为k3，垂直传染率为q，脉冲接种周期为T，最大潜伏期为τ，健康人的接种率为p，人口出生率为b，上述所有系数均为正数.

1 无病周期解的存在性

研究该模型的无病周期解，设E1=0,E2=0,I=0，于是可以得到相应的系统.

通过上面的脉冲微分方程得到系统（1）的无病周期解(S～,0,0,0,V～,R～).

2 无病周期解的全局吸引性

定理1 当R1＞1，R2＞1时，系统（1）全局吸引，其中

定理1的证明 在系统（1）中，可以得到脉冲不等式

考虑脉冲比较方程

存在一个整数k1＞0，使得当k1T＜t＜(k1+1)T时，有

根据系统（3）和系统（1）中第4个方程，可得：

由已知R1＞1，则

现实中，健康者初次感染病菌后，有90%的潜伏者不能够转移成为乙肝病人，所以E1＞E2，同时令I=0，由系统（1）中第2个方程可得，又由R2＞1，可得；同理，由系统（1）中第3个方程得，有

因此，当t→∞时，I→0,E1→0,E2→0.不妨设I＜ε1,E1＜ε2,E2＜ε3，其中εi,i=1,2,3都是任意小的正数，由系统（1）第1、第5个方程得

分析脉冲比较方程

根据脉冲比较定理，存在一个整数k2＞0，使得当k2T＜t＜(k2+1)T时（k2＞k1），有

3 疾病的持久性

定理2 当R3＞1时，系统（1）是持久的，其中

定理2的证明 首先证明对于任意的t0＞0，不可能对所有的t＞t0，存在I*＞0，都有I(t)≤I*.假设令t=t1时，I(t1)=I*.∀ε＞0，当t1＜t＜t1+ε时I(t)＜I*，此时I′(t)＜0.

根据系统（1）中第1个方程和第5个方程有：

分析脉冲比较方程

与前同理，脉冲比较方程可得：

根据脉冲比较定理，存在一个整数k3＞0，使得当k3T＜t＜(k3+1)T时，有

由系统（4）和系统（1）的第4个方程可得：

由R3＞1知，I′(t)≥0，可知矛盾，所以，存在t＞t0，有I(t)＞I*成立.

因此我们可以考虑两种情况［8-9］：

1）当t充分大时，I(t)≥I*；

2）当t充分大时，I(t)围绕I*振动.

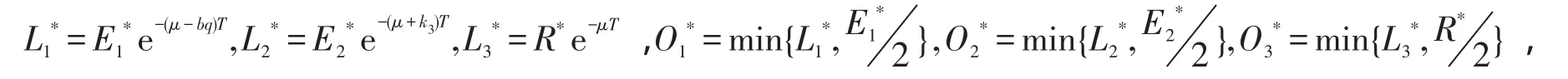
设t=t1时，令与I(t)有下界性证明同理，可得由系统（4）可知S(t)≥m1,V(t)≥m2.由上所述，系统（1）是持久的.

4 结论

在具有脉动接种和垂直传染的SEIVR乙肝模型研究中，当R1＞1，R2＞1时，无病周期解全局吸引.在R1，R2表达式可以看出，随着感染率β,β1,垂直传染率q的减小，恢复率k1,k2的增大，乙肝疾病将可能被消亡，这是个理想状态.在系统（4）中，，可以得到，即通过提高疫苗接种率p的数值，可得R3＞1，使得疾病持久.因此控制疾病的大规模爆发，乙肝疫苗的大规模接种和疾病传染率、垂直传染率的数值减少是控制乙肝病毒感染有效手段.

［1］杨金根，李学志.带有脉冲接种和时滞的乙肝模型的稳定性分析［J］.数学的实践与认识，2013，43（12）:141-149.

［2］杨金根，李学志，张喜来.带脉冲接种和垂直传染的时滞的乙肝模型［J］.应用泛函分析学报，2013，15（1）:66-71.

［3］罗丽丽，孟改利，翼贞浩，等.乙肝疫苗接种后体液的免疫应答模型［J］.数学的实践与认识，2011，15:1-11.

［4］LuJiu，Zhang Xiaoqiang，Zhou Yicang.Tuberculosis model with seasonality［J］.B Math Biol，2010，72:931-952.

［5］Stone L，Shulgin B，Agur Z.Theoretical examination of the pulse vaccination policy in the SIR epidemic model［J］.Math Comput Modeling，2003，31（4）:207-215.

［6］Onofrio A.Stability properties of pulse vaccination strategy in SEIR epidemic model［J］.Math Biosci，2002，179:57-72.

［7］Zhou Y，Liu H.Stability of periodic solutions for an SIS model with pulse vaccination［J］.Mathematical and Compute Modeling，2003，318:299-308.

［8］黄灿云，安小峰.一类具有多时滞和非线性发生率的脉冲接种SEIRS传染病模型［J］.兰州理工大学学报，2011，37（1）：121-125.

［9］杜艳可，徐瑞.一类具有时滞和脉冲接种的SEIRS传染病模型［J］.北华大学学报：自然科学版，2011，12（3）：258-264.