激光三角法在物面倾斜时的测量误差研究*

李冬冬，王永强，许增朴，周聪玲

(天津科技大学 机械工程学院，天津300222)

0 引 言

汽车变速箱中的倒角齿轮是传动系统中的关键部件，倒角轮廓的精度是评价齿轮加工的重要数据。测量方法主要分为接触式和非接触式两种，接触式测量是采用坐标测量机的探针触划齿轮倒角的表面，沿轮廓进行扫描采集数据点，测量精度高但容易划伤工件表面。非接触测量现在已有多种方法，其测量速度快、避免划伤工件等特点，使其应用越来越广泛，如视觉图像处理法、光干涉法等。由于齿轮倒角是平面尖角，存在一个倾斜角度，激光位移传感器的精度是指当待测面与发射光线垂直测量时的精度，而当平面有倾斜时会产生一定的误差，在精密测量中不能忽略。哈尔滨工业大学金洪禹等人，基于光散射原理研究了物面倾斜角与激光三角位移计光电接收面上汇聚光斑的光能质心之间的关系，推导出了理想模型的方程［1］，还有学者定性研究了激光测量系统的误差［2，3］，但不足以满足应用要求，因此，需要进一步研究激光三角法测量倾斜角度时的误差。

本文采用激光三角法，用激光位移传感器进行测量，结果表明:激光传感器在测量倾斜物面时仍能保证测量精度。

1 激光位移传感器测量原理

直射式激光三角法测量原理如图1 所示，激光器发射光线，经过会聚透镜后入射到被测物体的表面，物体移动或者表面形状发生改变后会导致光斑沿着入射光轴移动。若光斑在探测器光敏面上移动x'，利用相似三角形各边之间的比例关系，可以求出被测面的位移

图1 激光三角法测量原理图Fig 1 Measurement principle of laser triangulation

2 激光位移传感器的测量精度

将激光位移传感器Keyence LK—G30 固定在水平支架上，光点投射方向垂直向下;把标准量块水平放置在激光器正下方的平台上;二者都使用水平仪校准安装面状态是平行的，分别用1，2，4 mm 三种块规多次测量，结果见表1。

表1 水平面上标准量块测量数据Tab 1 Standard gauge block measurement datas on horizontal plane

从表1 结果可以看出:测量标准量块时，最大误差为3 μm，统计10 次数据求平均值分别是1.000 7，2.001 1，4.000 9 mm;故知激光位移传感器在测量标准平面的误差为1 μm，满足高精度测量要求。

3 激光三角法测量倾斜平面

3.1 倾斜平面测量误差的来源

激光位移传感器的假设是发射光束始终与被测物表面法线方向相一致，在实际测量中发射光束与被测表面的法线方向是不完全一致的，存在一个角度。被测表面倾斜角的不同，入射光点所产生的散射光空间分布将发生变化，从而使接收透镜接收到的光能量发生变化，这就使得光电接收面上的像光斑的光能质心相对其几何中心产生偏移。成像面上的CCD 检测的是投射到其上的光斑的光能质心的位置，而不是其几何中心的位置，这种变化造成实际测量值与测量原理的计算值会产生一定偏差，即待测平面倾斜带来了测量误差。

3.2 倾斜角度测量实验设计

激光位移传感器测量倾斜平面的实验系统如图2 所示。当激光位移传感器发射光线垂直照射在标准量块的平面上，测距最精确，记录此时数值L0;当步进电机驱动旋转平台(步进旋转电机重复精度0.004°)转过一个角度，那么激光传感器上记录一个测量值Lk(k=0，5，10，...)，则Lk－L0的绝对值就是量块上的光点移动的距离。每次旋转固定角度α，根据解析几何也可算出一个光点位移理论值x。激光传感器安装在运动平台上，偏移旋转电机中心轴线(也是量块中心线)2 mm 进行测量，比较二者即可得出激光位移计测量倾斜平面时的误差。

测量值

L=Lk－L0

计算值

用步进电机控制旋转平台带动量块可以进行顺时针旋转和逆时针旋转，每次转动5°进行测量，上传到计算机处理，测量与误差曲线，如图3 所示。

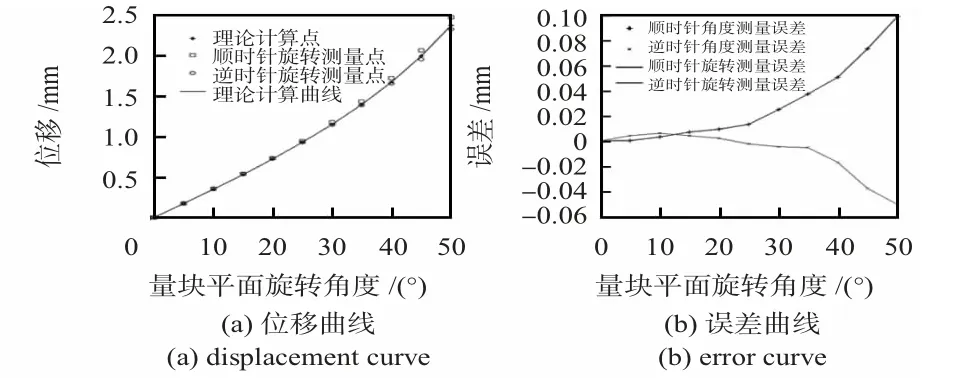
图3 测量与误差曲线Fig 3 Measurement and error curve

分析可知，在顺时针和逆时针倾斜转角各0°～50°的范围内，激光传感器的位移一定时，随着转角的增大测量误差也在增大，并且呈现非线性，这与其设计原理是一致的。在倾斜角度相同时，顺时针转角测量的误差一般比逆时针转角测量误差要稍大，在50°时，误差分别为100，50 μm，这对一些精密测量来说是不能忽视的。

由测量数据进行误差补偿，采用最小二乘法拟合离散点，残差分布如图4 所示。

图4 误差补偿后的残差曲线Fig 4 Curve of residual error after error compensation

进行误差标定后，绝大部分残差均在±2 μm 内，最大残差为－6 μm，分布区间为［－6，5］μm;标定后显著的减小了工件表面倾斜对激光位移传感器的影响，误差极小，证明实验测量系统可以用于非接触式精密测量和倾斜物面检测。

4 结 论

本文利用实验平台测量系统，对激光位移传感器的精度进行了测定，在工件表面倾斜时，对激光位移传感器进行了误差的实际测量，利用不同倾斜角度的数据建立了0°～50°范围内的误差—倾斜角的映射关系，并进行了误差补偿。结果表明:建立误差补偿后最大残差为6 μm，提高了实验系统的测量精度和适用性。实验中通过旋转电机测得当量块平面倾斜角大于50°时，激光位移传感器的测量数据虽然在量程内，但并不稳定;当大于57°时，所用型号的激光传感器已不能正常接收到物面返回的散射光，故无法显示数据，这点可供参考使用。

［1］ 金洪禹.基于光散射的三角法测量技术的研究［D］.哈尔滨:哈尔滨工业大学，2006.

［2］ 吴剑锋，王 文，陈子辰.激光三角法测量误差分析与精度提高研究［J］.机电工程，2003，20(5):89－91.

［3］ 黄战华，蔡怀宇，李贺桥，等.三角法激光测量系统的误差分析及消除方法［J］.光电工程，2002，29(3):58－61.

［4］ 杨耀权，施 仁.激光扫描三角法大型曲面测量中影响参数分析［J］.西安交通大学学报，1999(7):15－18.

［5］ 冯俊艳，冯其波，匡翠方.高精度激光位移传感器的技术现状［J］.应用光学，2004，25(3):33－36.

［6］ 蔡春明.基于视觉引导的激光齿轮倒角测量系统研究［D］.天津:天津科技大学，2013.

［7］ 周 坤，季海焦，刘海滨.激光三角法测量中被测物表面特性对测量精度影响的分析［J］.光学与光电技术，2009，7(2):70－73.